Kvanttilaskennan aakkoset
osa A
Näet tämän tekstin, jos et ole kirjautunut TIMiin. Voit katsoa videoita, mutta et voi tehdä tehtäviä. Voit kirjautua sisään TIMiin tästä:
Edessäsi oleva Kvanttilaskennan aakkosten A-osa on ensimmäinen kurssisarjan osio. A-osassa keskitytään olennaisiin käsitteisiin, joita tarvitaan kvantti-informaation ja kvanttilaskennan ymmärtämiseksi. Kvanttifysiikkaa tuomme mukaan pikku hiljaa muiden asioiden lomassa. Varsinaiseen kvanttifysiikan matemaattiseen teoriaan perehdytään vasta myöhemmissä osissa, eli tässä A-osassa et juurikaan matematiikan tietoja tarvitse. Sen sijaan eteen tulee useita uusia käsitteitä. Mieti tarkasti käsitteiden sisältöjä ja niiden yhteyksiä.
Kurssi koostuu kokonaisuudessaan tästä yhdestä vuorovaikutteisesta dokumentista. Tietoa tarjoillaan sekä videoina että tekstinä. Kurssin alkupuolella videoita ja tekstiä on enemmän, kun taas loppupuolella vuorovaikutteisten harjoitusten määrä kasvaa. Kurssi perustuu suurelta osin tekemällä oivaltamiseen ja vaatii sinulta aktiivista otetta opiskeluun. Keskity harjoituksiin äläkä lannistu, vaikka jokin tehtävä vaatisi useamman yrityskerran. Loppuosassa pääset ohjelmoimaan kvanttitietokoneen simulaattoria!
Dokumentissa olevat videot erottaa muista kuvista oikean alalaidan symbolista . Voit säätää videoiden nopeutta ja halutessasi laittaa tekstityksen päälle. Namiskat löytyvät videon alalaidasta ja ruudun alta kun laitat videon pyörimään.
Dokumentin osista ja rakenteesta:
- Jotkut sanat ovat tärkeämpiä kuin toiset. Avainsanat ovat tällaisia pulskia ja tummansinisiä. Sanalista löytyy dokumentin yläpalkista.
- Kokeile itse-laatikoissa pääset tekemään jotakin itse. Älä pidä kiirettä näiden kohtien kanssa, vaan mieti rauhassa mistä laatikossa kerrotussa asiassa on kyse.
- Oppimisen avuksi tekstin joukossa on kysymyksiä. Kysymykseen voit vastata kerran. Ei kannata lähteä arvailemaan, vaan palaa tekstiin ja videoihin jos et tiedä vastausta. Kysymykset ovat oppimisen tueksi eikä niissä väärin vastaaminen kaada kurssin suoritustasi.
- Pisteitä saat pureksimalla kirpeän maukkaita tehtäviä. Tehtäviä saa tehdä niin monta kertaa, kuin on tarvis. Joissakin tehtävissä sinun tulee saada vastattua kolme kertaa peräkkäin oikein. Kurssin suorittamiseksi kaikki tehtävät tulee tehdä loppuun asti.
- Kivistä opinpolkua on pehmustettu ohjeilla ja vinkeillä. Nämä tunnistat vihreästä väristä. Voit sivuuttaa tällaisen kohdan jos et koe sitä tarvitsevasi. Välillä on myös tarjolla lisätietoa ja nekin on merkitty vihreällä.
Näitä ohjeita ei tarvitse opetella ulkoa, vaan homma etenee omalla painollaan. Dokumentin alkupuolella Kvanttipöllö muistuttelee sinua dokumentin eri osien merkityksestä.
Kvanttipöllön ohje
Sivun oikeassa reunassa on oransseja palkkeja. Oranssi palkki on merkkinä lohkosta, jota et ole vielä lukenut. Palkkia klikkaamalla voit merkitä kohdan luetuksi. Mikäli opettaja tekee korjauksia ja kappale muuttuu sen jälkeen kun olet sen lukenut, näkyy palkki keltaisena. Saat tällaisen Kvanttipöllön ohjeen piiloon klikkaamalla pöllöä. Vinkit ja lisätietolaatikot ovat kiinni ja aukeavat pöllöä klikkaamalla.
Alla on listattuna yksityiskohtaisempia ohjeita. Jos sinulla on jo hinku aloittaa kurssi, niin voit hypätä niiden yli ja palata vasta tarvittaessa.
Oikea marginaali on varattu omille merkinnöillesi. Voit kirjoittaa muistiinpanoja itsellesi (Just me) tai havaintoja myös muiden näkyville (Everyone). Klikkaa ensin tekstiä. Jos menu on oikealla (oletus), saat kynän kuvasta esiin menun ja valitse sieltä 'Comment/Note'. Jos menu on vasemmalla, niin saat näkyviin C-kirjaimen kommentointa varten.
—Kurssin kaikki materiaali on kurssidokumentissa. Kurssin suorittamiseksi käy läpi kurssin koko aineisto ja erityisesti
testaa kaikkia kokeile itse -laatikoita
vastaa kaikkiin kysymyksiin (väärin vastaaminen ei haittaa)
tee kaikki tehtävät loppuun asti
aivan lopuksi pohdi oppimaasi ja kiteytä pääkohdat muutamaan lauseeseen
Klikkaa Tallenna toimintasi jälkeen aina kun sellainen on laatikon sisällä. Näin tekemisesi kirjautuu. Tallentaminen saa aikaan myös vastauksesi tarkistuksen. Jos vastauksesi on väärä, niin tehtävien kohdalla jatka yrittämistä.
Kysymykseen voit vastata vain kerran, joten ei kannata lähteä suin päin arvailemaan. Jos olet epävarma, niin palaa tekstiin ja videoihin tai kysymykseen liittyvään 'kokeile itse' -laatikkoon. Toki väärin vastaaminenkaan ei haittaa, vaan silloin tiedät tarvitsevasi kertausta. Kysymysten tarkoituksena on antaa sinulle mahdollisuus testata, että olet ymmärtänyt asian.
Tehtäviä saa tehdä niin monta kertaa, kuin on tarvis. Tehtävien avulla saat harjoiteltua kurssin asioita. Tyypillisesti tehtävässä haettu oivallus vaatii kokeiluja. Porttitehtävän tullessa vastaan ala pelottomasti kokeilla kaikkia sen sallimia portteja ja syötteitä. Pääsääntöisesti kannattaa tehdä tehtävät loppuun asti sitä mukaa kun niitä tulee. Voit toki jättää myös jonkin hankalan tehtävän hautumaan ja palata siihen myöhemmin. Kurssin läpäisemiseksi kaikki tehtävät tulee olla tehtynä.
Suorituksesi voit tarkistaa dokumentin lopusta, jossa on listattuna vastaamattomat kysymykset ja tekemättömät tehtävät.
Sivun oikeassa reunassa on näkyvissä oransseja palkkeja. Oranssi palkki on merkkinä lohkosta, jota et ole vielä lukenut. Oranssia palkkia klikkaamalla voit merkitä kohdan luetuksi. Klikkaamalla ![]() saat merkittyä luetuksi dokumentin lohkot edelliseen otsikkotasoon asti. Jos et pidä palkeista, voit poistaa ne kokonaan käytöstä klikkaamalla ratasta -> Merkitse kaikki luetuksi. Palkit ovat kuitenkin suositeltava tapa pitää kirjaa omasta etenemisestäsi, joten kannattaa ainakin kokeilla niiden käyttöä.
saat merkittyä luetuksi dokumentin lohkot edelliseen otsikkotasoon asti. Jos et pidä palkeista, voit poistaa ne kokonaan käytöstä klikkaamalla ratasta -> Merkitse kaikki luetuksi. Palkit ovat kuitenkin suositeltava tapa pitää kirjaa omasta etenemisestäsi, joten kannattaa ainakin kokeilla niiden käyttöä.
Jos tarvitset apua kurssin tehtävissä tai haluat tarkennusta johonkin asiaan, niin oikea paikka kysymyksille on kurssin keskustelupalsta. Keskustelupalstalle pääset yläpalkin Keskustelu-kohdasta.
Moneen tehtävään löytyy jo valmiiksi vinkkiä tehtävän alapuolelta klikkaamalla vihreää pöllöä. Jos jäät jumiin, niin kysy neuvoa keskustelupalstalla. Kannattaa ensin silmäillä aikaisempaa keskustelua läpi, sillä joku muu on saattanut jo kysyä samaa asiaa.
Tiettyyn tehtävään viittaaminen on kätevää esimerkiksi silloin, kun haluat kysyä siitä keskustelupalstalla.
Kysymyksen, tehtävän ja muidenkin osioiden oikeassa yläkulmassa on symboli #. Tämä on linkki kyseiseen osioon. Kun viet hiiren symbolin päälle, selaimesi näyttää linkin osoitteen ruudun alareunassa tai osoitepalkin lähellä. Osion nimi on se, mikä on osoitteessa #-merkin jälkeen. Voit myös klikata linkkiä. Silloin näet osion nimen osoitepalkissa ja siitä se on helppo kopioida.
Esimerkiksi A-osan ensimmäisen tehtävän nimi on #tehtava-jakaumat.
- Lue videon vieressä tai alla (riippuen mitä laitetta käytät) olevat saatesanat ajatuksella ennen kuin alat katsoa videota.
- Speed -kohdasta voit säätää videon nopeutta.
- Adv -valinnasta saat näkyviin hyppäykset eteen ja taakse.
- Tekstityksen saat päälle kolmen pisteen takaa (Chrome) tai CC-ikonista (Firefox).
- Hide file-painikkeesta saat videonäkymän pois sen katsottuasi.
Kvanttilaskennan aakkoset käyttää alustanaan TIMiä. TIM (The Interactive Material) on monipuolinen oppimisalusta, jonka avulla voidaan luoda interaktiivisia oppimateriaaleja. TIM on avoimen lähdekoodin ohjelmisto, jonka ylläpidosta vastaa Jyväskylän yliopiston Informaatioteknologian tiedekunta. Enemmän tarinaa TIMistä löytyy täältä. Tällä kurssilla olennaista on se, että tässä TIM-dokumentissa on erilaisia interaktiivisia tehtäviä. Lisäksi voit muokata jonkin verran dokumentin näkymää mieleiseksesi. Vasemman yläkulman kirjan kuvasta saat sisällysluettelon näkyviin.
Kurssin järjestäjälle voit lähettää sähköpostia osoitteeseen kvanttiaakkoset@jyu.fi. Kurssin lopussa on myös palautelomake, jolla parannusehdotukset menevät perille.
Kvanttiaakkosten A-osa on tehty Jyväskylän yliopiston IT-tiedekunnassa. Kurssin TIM-toteutuksen ovat suunnitelleet Teiko Heinosaari, Juha Reinikainen ja Vesa Lappalainen. Juha, Vesa ja TIM-tiimi ovat rakentaneet tarvittavat palikat TIMiin. Kurssin materiaalin on suunnitellut ja kirjoittanut Teiko. Videot Teiko on kuvannut yhdessä Jari Niemen ja Joni Palmirannan kanssa. Jari ja Joni ovat editoineet videot. Videoiden kansikuvat on tehnyt Aino Sutinen.
A.1 Mitä on kvanttifysiikka?
Aloitamme kurssin lyhyellä johdatuksella kvanttifysiikkaan.
A.1.1 Kvanttifysiikan alku
Fysiikka on tieteenala, joka pyrkii ymmärtämään maailmankaikkeutta ja sen ilmiöitä perustavanlaatuisella tasolla sekä kehittämään teorioita näiden kuvaamiseksi ja ennustamiseksi. Fysiikalle tyypillistä on se, että tarkasteltavat asiat voivat olla kooltaan hyvin pieniä, kuten atomit ja alkeishiukkaset, tai hyvin suuria, kuten vaikkapa galaksit ja mustat aukot.
Fysiikka jaotellaan karkeasti klassiseen fysiikkaan ja moderniin fysiikkaan. Klassinen fysiikka pitää sisällään mekaniikan, termodynamiikan ja sähkömagnetismin. Mekaniikka tutkii kappaleiden liikettä ja liikkeen aiheuttavia voimia. Termodynamiikka käsittelee lämpöä ja energian muutoksia. Sähkömagnetismi taas tarkastelee sähkö- ja magneettikenttiä sekä niiden vaikutusta varattuihin kappaleisiin.

Modernin fysiikan peruspilarit ovat kvanttiteoria ja suhteellisuusteoria, jotka syntyivät 1900-luvun alkuvuosikymmeninä. Moderni fysiikka on siis jo sata vuotta vanhaa fysiikka. Kyseessä on käyttöön jäänyt nimitys, joka kuvasi siirtymistä uuteen ajattelutapaan verrattuna aikaisempaan. Toisaalta kvanttifysiikkaa ja suhteellisuusteoriaa tutkitaan ja kehitetään edelleen. Vaikka näiden teorioiden kehykset tunnetaan, on niissä silti paljon tutkittavaa. Ymmärryksemme ja tietämyksemme on kehittynyt paljon sadassa vuodessa, ja kehittyy edelleen. Niistä on lisäksi versonut uusia fysiikan alalajeja, kuten hiukkasfysiikka ja ydinfysiikka.
Fysiikan tutkimus jaetaan tyypillisesti kokeelliseen ja teoreettiseen tutkimukseen. Tähän tutkimusmenetelmien jakoon perustuen on käytössä nimitykset kokeellinen fysiikka ja teoreettinen fysiikka, vaikka samasta tieteenalasta on kyse. Nämä ovatkin tiivisti yhteydessä toisiinsa ja ne etenevät käsi kädessä, välillä keskittyen samoihin tutkimusongelmiin ja välillä toisiaan kirittäen. Fysiikan ala laajenee uusiin suuntiin erityisesti silloin, kun tehdään sellaisia havaintoja, joita vanhat teoriat eivät pysty riittävän hyvin selittämään. Toisaalta uudet teoriat ohjaavat etsimään uusia ilmiöitä jollakin uudella tavalla tai uudesta näkökulmasta. Fysiikan tutkimuksessa kokeellinen ja teoreettinen lähestymistapa ovat pitkälle kehittyneitä ja yhtälailla tärkeitä. Molemmilla oli oma roolinsa myös kvanttifysiikan syntymässä. Nykyisin tietokoneiden kehittymisen myötä voidaan lisäksi erottaa laskennallinen fysiikka kolmanneksi lähestymistavaksi, ja siitä on tullut tärkeä osa kvanttifysiikankin tutkimusta kokeellisen ja teoreettisen tutkimuksen lisäksi.
Kvanttimekaniikka oli aluksi pienten kappaleiden, erityisesti atomien, käyttäytymistä selittävä teoria. Myöhemmin ymmärrettiin, että joissakin tilanteissa myös suurten kappaleiden fysiikka vaatii kvanttimekaniikan periaatteiden käyttämistä. Esimerkiksi mustien aukkojen ominaisuuksien selittäminen ei onnistu ilman kvanttimekaniikkaa. Kvanttimekaniikka ei siis enää tarkoita ainoastaan pienten kappaleiden fysiikkaa. Tietyissä olosuhteissa tai tilanteissa fysiikka on erilaista kuin klassinen fysiikka, oli sitten kyseessä iso tai pieni kappale.
Kvanttipöllön ohje
Alla on ensimmäinen kysymys. Voit vastata kysymyksiin vain kerran. Jos et tiedä vastausta, niin kannattaa katsoa video uudestaan. Väärin vastaaminenkaan ei tosin ole niin vakavaa.
A.1.2 Systeemi, tila ja mittaus
Fysikaalisella systeemillä tarkoitetaan jotakin kokonaisuutta, jonka toimintaa pyritään ymmärtämään fysiikan avulla. Fysikaalinen systeemi on harvoin muusta maailmasta erillään, mutta fyysikko jakaa mielessään maailman tarkasteltavaan systeemiin ja sen ympäristöön. Tämä jako riippuu täysin siitä, mistä seikoista ollaan kulloinkin kiinnostuneita. Systeemi vuorovaikuttaa ympäristönsä kanssa silloin kun systeemin toiminta muuttuu jollakin tavoin ympäristön vaikutuksesta. Ympäristöä ei siis tarvitse sivuuttaa, mutta tyypillisesti olemme kiinnostuneet siitä miten ympäristö vaikuttaa systeemiin, emme siitä miten systeemi muuttaa ympäristöä.

Fysiikan lähtökohtana on se, että tutkittavana olevaa systeemiä havainnoidaan. Havainnoista on pyrkimyksenä löytää säännönmukaisuutta. Säännönmukaisuus voi tarkoittaa esimerkiksi sitä, että jotakin asiaa muuttamalla jokin toinen asia muuttuu samassa suhteessa. Analysoimalla säännönmukaisuuksia voidaan pystyä muodostamaan fysiikan teoria jostakin asiakokonaisuudesta tai ilmiöstä. Voikin sanoa, että fysiikan teorian tavoitteena on yhdistää havaintojen joukko johdonmukaiseksi ja yleispäteväksi järjestelmäksi.
Palataan vielä siihen kylmään juomaan, jonka olet viilentänyt jääpaloilla. Oletko kokeillut juoda sitä metallipillillä? Metallipilli tuntuu kylmemmältä kuin pahvinen pilli. Johtuikohan se eri juomista, vuoroveden korkeudesta tai viikonpäivistä? Tekemällä systemaattisia havaintoja erilaisissa tilanteissa voit todeta, että ero johtuu todellakin pillin materiaalista. Vielä asiaa lisää tutkimalla voisit löytää riippuvuuden lämmön siirtymisen nopeuden ja eri materiaalien välillä. Olennaista tällaiselle tutkimiselle on tehdä useita havaintoja ja analysoida niitä huolella. Kun ilmiön ymmärtää, voi löydetyn säännönmukaisuuden avulla ennustaa tapahtumien kulun kaikissa vastaavissa tilanteissa.
Järjestelmällisten havaintojen tekeminen on täysin keskeistä fysiikassa. Havainnoinnin jäsentämiseksi on hyödyllistä ottaa käyttöön käsitteet tila ja mittaus. Ne ovat etenkin kvanttifysiikassa tärkeitä, joskin ne toki kuuluvat muuhunkin fysiikkaan. Nämä kaksi käsitettä tulevat olemaan tällä kurssilla kvanttifysiikan oppimisen lähtökohtana.
Videolla puhuttiin termodynamiikasta. Onko sana sinulle vieras?
Termodynamiikka on fysiikan osa-alue, joka käsittelee energian, lämmön ja työn muutoksia fysikaalisten systeemien välillä. Lämpötila, tilavuus, paine ja niiden muutokset ovat usein olennaisia termodynamiikan tarkasteluissa. Esimerkiksi auton polttomoottori, jossa polttoaineen palamisesta saatava energia muutetaan mekaaniseksi liikkeeksi, on tyypillinen termodynaamikan sovellus.
Perusasetelma fysikaalisesta kokeesta on kuvattuna alla. Fysikaalinen systeemi valmistellaan mittausta varten. Tätä tapahtumaa kutsutaan preparoinniksi, ja sen seurauksena systeemi on jossakin tilassa. Kutsumme tätä alkutilaksi. Alkutila voi olla tunnettu tai tuntematon, kunhan samanlaisella preparoinnilla voidaan toistaa koejärjestely. Lähtökohtaisesti fysiikka kuvaa tilanteita, joita voidaan toistaa. Jokaisella toistokerralla mittalaite antaa mittaustuloksen.
Tilanteessa voi olla myös kolmas eroteltavissa oleva osatekijä. Preparoinnin jälkeen systeemi voi vuorovaikuttaa ympäristön kanssa joko kontrolloidusti tai itsestään, osittain hallitsemattomasti. Tätä vuorovaikutusta voimme yleisesti kutsua prosessiksi. Ajallisesti prosessi tapahtuu ennen mittausta.
Prosessissa systeemin tila muuttuu. Prosessi voi olla tarkkaan suunniteltu tapahtuma, jossa systeemin annetaan hallitusti vuorovaikuttaa ympäristön kanssa ja mm. vuorovaikutuksen kestoa ja voimakkuutta säädellään. Prosessi voi myös olla hallitsematon tapahtuma, jossa systeemi pääsee vuorovaikuttamaan ympäristön kanssa tavalla, joka haluttaisiin välttää. Tyypillisesti tämä tarkoittaa sitä, että systeemin tilaan tulee melua tai hälyä. Prosessi saattaa pitää sisällään kumpiakin tapahtumia, hallittuja ja hallitsemattomia.
Joskus saatetaan olla kiinnostuneita systeemin tilasta myös mittauksen jälkeen. Joissakin mittauksissa systeemi menetetään mittauksessa. Tällainen on esimerkiksi fotonin paikan mittaaminen, jossa fotoni tuhoutuu havaitsemisen seurauksena. Joissakin toisissa mittauksissa systeemi saattaa säilyä (ks. kuva alla). Tällöin täytyy kuitenkin muistaa, että systeemin tila voi muuttua mittauksessa. Mittauksen jälkeisen tilan voi pystyä päättelemään saadusta mittaustuloksesta, mutta näin ei aina ole vaan tilan muutoksessa voi olla satunnaisuutta. Lähtökohtaisesti täytyy varautua siihen, että mittaus muuttaa systeemin tilaa. Mittauksessa saatu tieto systeemin ominaisuuksista liittyy siis systeemin tilaan ennen mittausta ja ainoastaan osittain mittauksen jälkeiseen tilaan.
Tämä kuvattu jako preparoinnin, prosessin ja mittauksen välillä ei ole yksinomaan kvanttifysiikalla ominainen tilanne, vaan kuvaa suurta osaa fysiikan kuvaamia asetelmia. Kvanttifysiikassa on kuitenkin oltava tavallista tarkempi siitä, minkälaisesta tilanteesta puhumme ja mitä käsitteillä tarkoitamme. Arkikokemuksemme ei auta samalla tavoin kuin vaikkapa heittoliikkeen mekaniikkaa tarkasteltaessa.
A.1.3 Kvanttifysiikan erityispiirteet
Klassisessa fysiikassa systeemit ovat joko kappaleita tai aaltoja. Pientä kappaletta kutsutaan myös hiukkaseksi. Kvanttifysiikan lakeja noudattava fysikaalinen systeemi käyttäytyy eri tavoin kuin mihin olemme tottuneet klassisessa fysiikassa. Tätä eroa korostaaksemme saatamme puhua kvanttisysteemistä kun tarkoitamme fysikaalista systeemiä, jonka toiminnan ymmärtämiseksi vaaditaan kvanttifysiikkaa. Kvanttisysteemi, kuten elektroni, ei ole hiukkanen klassisen fysiikan mielessä. Kvanttisysteemi ei myöskään ole aalto, vaikkakin sen käyttäytymisessä on tietynlaisissa kokeissa aaltomaisia piirteitä. Kvanttisysteemi on kokonaan uudenlainen systeemi, jota kannattaa pyrkiä ymmärtämään ilman liiallista kytköstä klassisen fysiikan kappaleisiin ja aaltoihin. Kvanttiteoria ei kerro kvanttisysteemin, kuten elektronin, kulkureittiä. Sen sijaan kvanttiteoriasta voi laskea todennäköisyydet sille, että elektroni havaitaan myöhemmin jossakin tietyssä paikassa. Tyypillisessä kvanttifysiikan koetilanteessa mahdollisia lopputilanteita on useita.
Kuten videolla tuli ilmi, kvanttisysteemin tilan voi ymmärtää kahdella yhtäpitävällä tavalla. Tilan voi joko ymmärtää preparoinnin kuvauksena, eli tietynlaisena reseptinä siitä, miten jokin preparointi suoritetaan. Vaihtoehtoisesti tilan voi ymmärtää matemaattisena kuvauksena (esim. taulukkona), josta kaikki systeemille mahdollisesti suoritettavien mittausten tulokset voidaan laskea. Puhumme myöhemmin lisää siitä, että kvanttiteoria ennustaa mittaustulosten todennäköisyysjakauman, ja tätä onkin syytä ajatella mittauksen lopputuloksena.
Kvanttisysteemin ominaisuuksiin liittyy siis se, että kvanttiteoria ei ennusta niiden tarkkoja arvoja vaan ainoastaan todennäköisyyksiä. Asiaan liittyy vielä toinenkin puoli, joka on ehkäpä hätkähdyttävämpi. Klassisella hiukkasella, eli hiukkasella joka noudattaa mekaniikan lakeja, on joka hetki tietty paikka ja nopeus riippumatta siitä, mitataanko nämä suureet vai ei. Toki tällaista väitettä voi olla mahdoton kokeellisesti testata, mutta oletus ominaisuuksien havaitsijasta riippumattomasta olemassaolosta ei ole ristiriidassa klassisen fysiikan kanssa. Myös arkikokemuksemme tukee ajatusta siitä, että tavallisten kappaleiden ominaisuudet ovat joka hetki määrättyjä.

Erona klassisen fysiikan tilanteeseen nähden kvanttisysteemiin liittyy aina ominaisuuksia, joilla ei ole määrättyä arvoa, vaan vasta mittauksessa jokin mahdollisista ominaisuuden arvoista tulee esille. Kvanttiteorian puitteissa olisi ongelmallista olettaa, että kvanttisysteemin kaikki ominaisuudet ovat määrätty jo ennen mittausta. Kvanttifysiikassa havaitsija tekee valinnan suorittaa tietty mittaus, ja näin hän saa jotakin tietoa kvanttisysteemin tilasta. Yksittäisestä mittaustuloksesta ei voi päätellä kvanttisysteemin tuntematonta tilaa, olipa mittaus millainen tahansa.
A.2 Satunnaisuus ja todennäköisyys
Kvanttifysiikassa tulevien tapahtumien ennustamiseen liittyy satunnaisuutta. Tyypillisessä kvanttifysikaalisessa kokeessa emme voi ennustaa lopputulosta täydellä varmuudella, vaan ainoastaan laskea mahdollisten vaihtoehtojen todennäköisyydet. Tämä seikka on yksi keskeisimmistä kvanttiteorian piirteistä ja sen vuoksi käsittelemme tässä jaksossa satunnaisuutta ja todennäköisyyttä.
A.2.1 Satunnaisuuden eri tasot
Arkikokemuksemme mukaan tuleviin tapahtumiin liittyy usein tiettyä satunnaisuutta. Saatamme puhua todennäköisyyksistä silloin, kun tietomme on puutteellista tai epävarmaa.

Jos olemme täysin varmoja jonkin tapahtuman kulusta, ei meidän tarvitse puhua todennäköisyyksistä lainkaan. Voimme esimerkiksi pitää varmana, että omena putoaa maahan kun heitän sen ilmaan. Tällaisissa tilanteissa fysiikka kertoo yksikäsitteisen lopputilanteen ja siihen johtavat vaiheet, tässä esimerkissä mm. omenan lentoradan ja lentoajan. Joissakin toisissa tilanteissa lopputuloksen ennustaminen olisi periaatteessa mahdollista, mutta käytännössä liian hankalaa tai vaivalloista. Nopan heittäminen on tästä hyvä esimerkki. Nopan ilmalento ja kieriminen pöydällä voidaan periaatteessa laskea mekaniikan liikeyhtälöiden avulla, mutta harvoin tiedämme kaikkia laskuun vaikuttavia seikkoja, kuten nopan asentoa ja alkunopeutta riittävän tarkasti.
Joidenkin kappaleiden fysiikka on niin monimutkaista, että niiden myöhempää tilaa on käytännössä mahdotonta ennustaa pitkällä aikavälillä. Itse asiassa jopa yksinkertaisen systeemin myöhemmän tilan ennustaminen voi olla erittäin haastavaa, jos tilan muutos on herkkä alkuarvoille. Tämä tarkoittaa, että pienen pieni ero kahden eri alkutilan välillä johtaa erilaisiin lopputuloksiin. Koska alkutilaa ei voi määrittää absoluuttisen tarkasti, on tällaisen alkuarvoherkkyyden seurauksena lopputilan ennustamisen mahdottomuus käytännön tasolla. Alkuarvoherkkyys on yksi kaaottisen systeemin keskeisistä tunnuspiirteistä. Kaaottisen systeemin käyttäytyminen saattaa näyttää satunnaiselta, vaikka se on periaatteessa ennustettavissa.
Osaatko edellisen videon katsottuasi kuvailla satunnaisuuden kolme eri tasoa ja antaa niistä esimerkit?
Kvanttipöllön ohje
Videot, joissa on kertausta tai lisäohjeita, eivät ole kansikuvan takana, vaan ne löytyvät tekstin seasta alla esitetyllä tavalla. Voit ohittaa ne, jos asia on sinulle jo selvä.
Muistele sitten vielä erityisesti se, mitä kvanttimittauksen satunnaisuudesta videolla sanottiin ja vastaa seuraavaan kysymykseen.
A.2.2 Todennäköisyyden matemaattinen kuvaaminen
Riippumatta siitä mistä satunnaisuus johtuu, kuvataan satunnaisuutta matemaattisesti todennäköisyyksien avulla. Todennäköisyysjakauma liittyy johonkin tilanteeseen tai tapahtumaan, jossa on useita eri vaihtoehtoja. Jokaisen mahdollisen vaihtoehdon todennäköisyys on luku nollan ja ykkösen väliltä, ja todennäköisyysjakauma listaa nämä luvut. Ääritapaukset 0 ja 1 liittyvät erikoistapauksiin:
- Jos vaihtoehdon todennäköisyys on 1, se tapahtuu varmasti.
- Jos vaihtoehdon todennäköisyys on 0, se jää varmuudella tapahtumatta.
Kun vaihtoehdot on valittu siten, että ne ovat toisensa poissulkevia mutta kokonaisuudessaan kattavia siinä mielessä, että muita mahdollisuuksia ei ole, on todennäköisyyksien summa 1. Todennäköisyysjakauma on siten lista luvuista, joista jokainen on nollan ja ykkösen välillä ja yhdessä ne summautuvat ykköseksi. Mitä suurempi todennäköisyys johonkin vaihtoehtoon liittyy, sitä varmemmin se tapahtuu.
Kuten videolla kävi ilmi, jonkin vaihtoehdon todennäköisyys kertoo sen, miten usein tuo vaihtoehto suhteellisesti tapahtuu toistokokeessa. Toistokoe tarkoittaa saman tapahtuman toistamista useita kertoja samankaltaisissa olosuhteissa. Mitä suurempi toistojen määrä on, sitä tarkemmin todennäköisyys kuvaa todellista tilannetta.
Todennäköisyysjakauma on kätevä esittää pylväsdiagrammin avulla. Alla oleva diagrammi on esimerkki sellaisesta todennäköisyysjakaumasta, jossa mahdollisia vaihtoehtoja on neljä. Pylvään korkeus kertoo vaihtoehdon todennäköisyyden. Voit viedä kursorin diagrammissa palkin päälle nähdäksesi tarkan luvun.
Yllä oleva todennäköisyysjakauma on listana kirjoitettuna [0.1, 0.2, 0.1, 0.6]. (Huomaa, että käytämme pistettä desimaaliluvuissa.) Alla on toinen todennäköisyysjakauma. Mikä se on listana kirjoitettuna?
Välillä todennäköisyyksiä ilmaistaan prosenttilukuina. Prosentti tarkoitta yhtä sadasosaa, eli 1%=0.01. Näin ollen todennäköisyysjakaumassa todennäköisyyksien summa on 100%.
Tarkastele alla olevia pylväsdiagrammeja. Yksi niistä ei ole todennäköisyysjakauma. Tunnistatko sen?
Kvanttipöllön ohje
Tämä on ensimmäinen tehtävä. Kurssin suorittamiseksi kaikki tehtävät tulee saada oikein. Voit yrittää niin monta kertaa kuin haluat. Tässä kyseisessä tehtävässä tulee saada kolme oikeata vastausta peräkkäin.
kirjoitusvirhe "Vielä tarvitaan 1 oikeata vastausta" - lisäksi uusi kierros nappi on sijoitettu käytettävyyden kannalta hankalasti tehtävälaatikkoa ennen
—A.2.3 Todennäköisyyteen pohjautuva tieto
Kuvittele, että ojennan sinulle nopan. Noppa on joko tavallinen tai se voi olla painotettu niin, että sillä ei voi saada viitosta eikä kuutosta. Et kuitenkaan tiedä kummanlaisesta nopasta on kyse.
Seuraavassa tehtävässä sinulla on kolme noppaa. Jokin nopista on viallinen siten, että se ei heittämällä anna kaikkia silmälukuja. Et tiedä mikä kolmesta nopasta on tuo viallinen kappale ja ainoa keino selvittää noppien ominaisuuksia on niiden heittely. Yhden heiton perusteella et voi vielä päätellä viallista noppaa. Voit toki pystyä arvaamaan sen, mutta se on silloin puhdas arvaus. Älä lähde arvailemaan, vaan heitä noppia niin monta kertaa, että voit varmuudella erottaa viallisen nopan.
Kun vaihtoehtojen määrä kasvaa, niin silloin on tyypillisesti suoritettava enemmän toistoja todennäköisyyteen perustuvan tiedon selvittämiseksi. Seuraavassa tehtävä on muuten samanlainen kuin edellä, mutta nyt noppia on kahdeksan. Samoin kuin aikaisemmassa tehtävässä, heitä noppia niin monta kertaa, että voit varmuudella erottaa viallisen nopan.
Kootaan vielä yhteen tässä jaksossa tekemämme havainnot. Nopan heitossa saatava silmäluku on satunnainen. Tavallisen nopan ja viallisen nopan silmälukuja vastaa erilaiset todennäköisyysjakaumat. Tämä ero ei tule esille yhdellä heitolla, mutta useamman heiton jälkeen voimme erottaa tavallisen ja viallisen nopan. Todennäköisyyteen pohjautuvia oletuksia tai väitteitä voidaan yleisemminkin testata toistamalla koetta tai havainnoimalla samanlailla toistuvaa tapahtumaa useasti.
A.2.4 Satunnaisuus kvanttimittauksen tuloksissa
Mittaaminen on keino saada tietoa fysikaalisen systeemin tilasta. Klassisessa fysiikassa, esimerkiksi mekaniikassa, teoria ei rajoita mittaustarkkuutta. Mittaustarkkuuteen vaikuttaa kuitenkin käytännön seikkoja eikä kaikkea epätarkkuutta voida poistaa, joten tyypillisesti mittausta toistetaan ja mittaustulokset ilmoitetaan tulosten jakaumana yksittäisen luvun sijaan. Teoriasta laskettua lukua voidaan sitten verrata jakaumaan. Onnistuneessa kokeessa mittaustulosten jakauma on kapea ja teorian antama luku jakauman keskellä. Mittaustuloksen satunnaisuus liittyy siis siihen, että mittaustarkkuus on rajallinen. Tästä syystä eri mittauskerroilla voidaan saada hieman eri mittaustulokset.
Kvanttimittauksella tarkoitamme kvanttisysteemille tehtävää mittausta. Kuten fysiikassa yleensäkin, kvanttimittauksen tarkoituksena on antaa tietoa tarkasteltavan systeemin tilasta. Mutta kvanttimittauksen tapauksessa yksittäisen mittauskerran antama luku ei kerro systeemin tilasta paljoakaan. Edes teorian kannalta mittauksen antamaa tietoa ei voi kiteyttää yhteen lukuun.
Tarkastellaan seuraavaksi kvanttimittausta, jolla on neljä mahdollista tulosta. Kun mittauksia tehdään monia kertoja, voidaan mittaustuloksista laskea todennäköisyysjakauma. Koska yksittäinen mittaustulos ei kerro paljoakaan, on mittaustulosten todennäköisyysjakaumaa parempi ajatella kvanttimittauksen varsinaisena lopputuloksena yksittäisen mittaustuloksen sijaan. Toki yksittäisellä mittauskerralla saamme jonkin mittaustuloksen, mutta ainoastaan mittausta toistamalla saadaan se tieto ulos, jonka kvanttimittaus voi tilasta kokonaisuudessaan antaa.
Alla on todennäköisyysjakauma, joka voisi kuvata kvanttimittauksen lopputulosta. Tässä tapauksessa mahdollisia mittaustuloksia on neljä.
Tällaisen kvanttimittauksen lopputulosta kuvaavan todennäköisyysjakauman kerääminen vaatii lukuisia mittauksen toistoja. Pylväsdiagrammi voi myös edustaa teorian avulla laskettua ennustetta kvanttimittauksen tulosten todennäköisyyksistä.
Kuvitellaan tilanne, jossa lähdet tekemään tiettyä kvanttimittausta ja toistat samaa koetta useaan kertaan. Kvanttisysteemi preparoidaan jokaisen mittauksen jälkeen takaisin alkutilaan, joten koetta toistetaan samanlaisena. Jokaisen mittauskerran jälkeen voidaan laskea mittaustulosten suhteellinen määrä ja tästä saadaan laskettua välivaiheen todennäköisyysjakauma. Tämä välivaihe lähestyy lopputulosta kun mittausta toistetaan riittävän monta kertaa, esimerkiksi tuhat kertaa. Jos toistojen määrä on pieni, välivaiheen todennäköisyysjakauma voi poiketa teoreettisesta todennäköisyysjakaumasta paljonkin. Välivaiheen todennäköisyysjakaumaa kannattaakin ajatella kirjanpitona saaduista mittaustuloksista. Siitä ei voi ennustaa tulevia mittaustuloksia.
Tarkastellaan seuraavaksi sitä, miten toistokokeesta lasketut suhteelliset määrät alkavat pikku hiljaa lähestyä varsinaista kvanttimittauksen lopputulosta kuvaavaa todennäköisyysjakaumaa.
Kvanttipöllön ohje
Tutustu rauhassa 'Kokeile itse' -laatikon asiaan ja tee siinä annettu harjoitus ajatuksen kanssa. Näitä harjoituksia ei pisteytetä, mutta ne pohjustavat jotakin tulevaa tehtävää.
Tässä kokeilussa huomasimme, että muutamasta mittauksesta laskettu todennäköisyysjakauma saattaa poiketa paljonkin varsinaisesta koko mittaustulostilastoa edustavasta todennäköisyysjakaumasta. Harjoitellaan pylväsdiagrammin tulkintaa vielä lisää. Alla olevassa tehtävässä on toisen kvanttimittauksen simulointi ja sen alla neljä eri todennäköisyysjakaumaa. Sinun tulee tehdä niin paljon mittauksia, että voit riittävällä varmuudella valita oikean todennäköisyysjakauman.
Kerrataan vielä tämän jakson opetus. Kvanttimittauksen antama mittaustulos on (erityistapauksia lukuun ottamatta) satunnainen, eli mittaustulos voi vaihdella mittauskerrasta riippuen. Kvanttiteoria ennustaa mittaustulosten todennäköisyysjakauman, ja tätä kannattaakin ajatella kvanttimittauksen varsinaisena lopputuloksena. Yksittäinen mittauskerta antaa vain yhden mittaustuloksen, eli oikean todennäköisyysjakauman selvittämiseksi tulee suorittaa useita mittauskertoja.
A.3 Informaatio
Informaatiolla tarkoitetaan tietoa, joka voi välittyä viestien, signaalien tai symbolien kautta. Informaation välittäminen muille on täysin olennaista lähes kaikessa ihmisen toiminnassa. Informaatio ei voi esiintyä yksinään ilman fysikaalista kantajaa. Tämän takia kvanttifysiikka tulee mukaan myös informaation käsittelyssä. Tässä jaksossa käymme läpi informaatioon liittyviä perusasioita.
A.3.1 Informaation määrä
Pitkän viestin lähettäminen tai tallentaminen on hankalampaa kuin lyhyen viestin, ja siitä syystä informaation määrän ymmärtäminen ja sopivalla tavalla kuvaaminen on tärkeää.
Kerrataan videolla tulleet pääkohdat. Informaation perusyksikkö on bitti. Matemaattisesti bitillä voi olla kaksi arvoa, 0 tai 1. Vaikka esimerkiksi tavallinen teksti ei koostu biteistä, voi sen halutessaan sopivalla muunnoksella muuttaa bittijonoksi. Bittijonossa informaation määrä on yksinkertaisesti siinä tarvittujen bittien lukumäärä. Bittien käyttäminen antaa siis yhtenäisen tavan vertailla eri lähteiden informaation määrää.
Informaation määrää on usein hyödyllistä ajatella siten, että haluat tehdä valinnan usean vaihtoehdon välillä ja ilmaista valintasi muille. Yhden bitin avulla voi ilmaista kyllä/ei -tyyppisen asian. Jalankulkijan liikennevalossa on kaksi vaihtoehtoa, vihreä valo ja punainen valo. Päällä olevan valon ilmoittaminen vaatii näin ollen yhden bitin verran informaatiota.
Kahden bitin avulla voi ilmaista valinnan neljän vaihtoehdon väliltä, sillä kahden bitin jonoja on neljä: 00, 01, 10 ja 11. Tällainen valintatilanne voi olla sellainen, jossa meillä on kaksi peräkkäistä kyllä/ei -asiaa, esimerkiksi kahdet jalankulkijan liikennevalot. Neljä vaihtoehtoa liittyy myös vaikkapa suunnan ilmaisemiseen neljän pääilmansuunnan tarkkuudella, jolloin voisimme kirjoittaa esimerkiksi 00 = pohjoinen, 01 = itä, 10 = etelä, 11 = länsi.

Kuten huomaat näitä tapauksia miettimällä, jokainen uusi bitti kertoo vaihtoehtojen määrän kahdella. Näin ollen neljä bittiä mahdollistaa valinnan 16:n eri vaihtoehdon välillä.
Viisi bittiä antaa mahdollisuuden valita jo 32:n eri vaihtoehdon välillä. Tämä riittää vaikkapa tietyn kirjaimen valintaan aakkosissa ja näin voisimme kääntää tekstin viiden bitin mittaisten palasien jonoksi. Näin itse asiassa tietoliikenteessä tapahtuukin: informaatio käännetään bittijonoksi, se lähetetään vastaanottajalle ja lopulta bittijono käännetään takaisin tekstiksi tai kuvaksi. Aakkosten lisäksi kirjoitetussa tekstissä käytetään useita erikoismerkkejä, kuten !, ? ja @. Nykyisin yleisesti käytetään 8 bitin merkkikoodistoa ja jokaisella 8 bitin pituisella jonolla voidaan ilmaista valinta 256:n merkin joukosta. Merkkikoodistoja on erilaisia, joten on aina tärkeä tietää mikä niistä on käytössä.
Olemme nähneet, että 2 vaihtoehtoa tarvitsee yhden bitin ja 4 vaihtoehtoa 2 bittiä. Entä jos vaihtoehtoja on 3, 5 tai jokin muu määrä, joka ei ole kahden monikerta? Kolmea vaihtoehtoa ei voi ilmaista yhden bitin avulla, mutta kaksi bittiä on siinä mielessä liikaa, että se riittää jo neljän vaihtoehdon ilmaisemiseen. On osoittautunut oikeaksi tavaksi mitata informaation määrää 2-kantaisen logaritmin avulla. Tätä emme tarvitse tällä kurssilla, mutta halutessasi voit lukea lisätietoa alta.
Kolme bittiä riittää ilmaisemaan kahdeksan vaihtoehtoa, sillä . Potenssimerkinnän avulla kirjoitettuna tämä on
, jossa siis bittien lukumäärä on eksponentissa. Yleisemmin
bittiä riittää ilmaisemaan
vaihtoehtoa.
Entä jos haluamme tietää tarvittavien bittien lukumäärän kun vaihtoehtojen määrä on annettu? Eksponenttifunktion käänteisfunktio on logaritmi. Informaation tapauksessa käytämme eksponentissa kantalukua 2 (sillä informaatio ilmaistaan bittien määränä), joten vastaava käänteisfunktio on 2-kantainen logaritmifunktio. Tämä määritellään siten, että kun on annettu positiivinen luku, niin
sillä luvulla
jolle
. Esim.
, sillä
. Tämän 2-kantaisen logaritmin arvo on määritelty kaikille positiivisille kokonaisluvuille. Alla olevalla laskurilla voit laskea sen arvoja eri tapauksissa.
Laskurilla voit varmistua, että tarvittavien bittien lukumäärä on kokonaisluku silloin, kun vaihtoehtoja on kakkosen monikerta (eli 2,4,8,16..). Muissa tapauksissa 2-kantainen logaritmi antaa desimaaliluvun.
A.3.2 Fysikaalinen bitti
Kun saamme uutta informaatiota, vaikkapa uutisia maailman tapahtumista, on useimmiten yhdentekevää miten tuon informaation saamme. Tieto on samaa tietoa, tuli se sitten tv-uutisista tai sanomalehdestä. Vaikka informaatio onkin tällä tavoin abstrakti asia, ei se voi esiintyä pelkältään, ilman jotakin fysikaalista kappaletta. Informaatiolla täytyy olla kantaja, eli jokin fysikaalinen systeemi, jonka tilasta pystymme lukemaan informaation. Fysiikan kannalta informaation lukeminen tarkoittaa systeemille suoritettavaa mittausta.

Yksinkertaisin viesti pitää sisällään yhden bitin verran informaatiota. Tässäkin tapauksessa bitillä täytyy olla jokin kantaja, eli fysikaalinen systeemi, jonka vaihtuvaan tilaan bitti on kirjoitettu. Tämä tarkoittaa, että viestin lähettäjällä on kaksi eri tapaa preparoida fysikaalinen systeemi ja viestin vastaanottaja pystyy mittauksella erottamaan ne toisistaan. Bitillä tarkoitetaankin myös jotakin systeemiä, jolla on kaksi toisistaan eroteltavissa olevaa tilaa ja näin mahdollisuus kantaa yhden bitin verran informaatiota. Tästä voidaan käyttää nimitystä fysikaalinen bitti, jos on tarpeen korostaa eroa ideaaliseen matemaattiseen bittiin.
Informaation kantajan valintaan liittyy monta eri puolta. Yksi tärkeä seikka on se, että informaatiota halutaan välittää luotettavasti ja tehokkaasti. Tottumuksemmekin ohjaavat valintoja. Sanomalehti ei välttämättä ole kovin tehokas tapa viestintään, mutta moni haluaa edelleen lukea uutiset paperisesta sanomalehdestä. Informaation säilyvyys ja alttius häiriöille ovat myös tärkeitä näkökantoja. Videolla puhuttiin kupin asennosta ja lämpötilasta viestinnän kannalta. Minkälaiset häiriöt vaikuttavat näihin kuvitteellisiin viestintätapoihin? Kupin lämpötila muuttuu ajan kuluessa huoneen lämpöiseksi ja näin ollen viesti ei pysy siinä pitkään. Toisaalta kuppi saattaa pudota pöydältä melko pienestäkin töytäisystä johtuen ja silloin sen asentoon perustuva viesti menetetään. Kupin lämpötila taas ei pudotuksesta juurikaan muuttuisi. Molemmilla viestintätavoilla on siis hyvät ja huonot puolensa.
A.3.3 Informaation prosessointi
Sekä viestinnässä että laskennassa informaatiota prosessoidaan, eli muokataan ja muunnellaan. Molemmissa tapauksissa valitaan aluksi tietty bittijono, sitten bittijonoa muokataan joidenkin sääntöjen mukaan ja lopuksi bittijono luetaan. Fysiikan näkökulmasta bittijonon lukeminen tarkoittaa, että informaatiota kantavalle systeemille suoritetaan mittaus. Aikaisempi havainnekuva fysikaalisesta koejärjestelystä toimii lähes sellaisenaan informaation prosessoinnin havainnollistamiseen. Lisäyksenä aikaisempaan kuvaan voimme ajatella preparointilaitteessa olevan valintanappeja, joilla tietty bittijono valitaan ja sitten fysikaalinen systeemi preparoidaan sen mukaisesti tiettyyn alkutilaan. Fysiikan kannalta prosessi muuttaa alkutilan toiseksi tilaksi. Informaation prosessointi on siten tilan muuntamista jollakin systemaattisella tavalla.
Prosessi voi koostua useista eri osavaiheista. Seuraavassa jaksossa harjoittelemme erilaisten prosessien rakentamista pienemmistä palasista.
Viestinnässä lähettäjä ja vastaanottaja ovat eri henkilöitä ja prosessi voi mallintaa vaikkapa viestintäkanavan melua. Tällaisessa yhteydessä prosessia kutsutaan kanavaksi. Esimerkiksi valoa voidaan lähettää optisen kuidun avulla, joka silloin on viestinnän kanava.
Tulemme jatkossa merkkaamaan kirjaimella q bittijonoa, joka valitaan ja jonka mukaan informaation kantajana toimiva fysikaalinen systeemi preparoidaan johonkin tilaan. Tämän jälkeen systeemi kulkee prosessin läpi mittaukseen. Näin ollen bittijono q on informaation prosessoinnin syöte. Jossain tapauksissa syöte on binääriluku, mutta syötteenä oleva bittijono voi myös olla merkkijono, jota ei tulkita binääriluvuksi.
Käytämme merkintää q[0] bittijonon ensimmäiselle bitille vasemmalta lukien, q[1] seuraavalle bitille, jne. Jos esimerkiksi q=100101110, niin tällöin q[0]=1 ja q[1]=0. Huomaa, että tietotekniikalle tyypilliseen tapaan alamme laskemaan bittien paikkoja alkaen nollasta. Harjoitellaan tätä merkintätapaa seuraavissa tehtävissä.
Bittien numerointijärjestys on tässä päinvastainen kappaleen "Binääriluvut" kakkosen eksponenttien eli bittien painojen järjestykseen nähden. Järjestysnumero ei tässä tarkoita eksponenttia, eivätkä nämä bittijonot välttämättä kuvaa lukuja. Kvanttipöllö: Joo, järjestys on tosiaan päinvastainen ja tämä on syytä huomata. Kuten huomautat, niin bittijono on tässä kohtaa vain merkkijono, joka ei välttämättä esitä lukua. Tässä kohtaa on valittu tämä järjestys siitä syystä, että ohjelmointikielissä on tapana laskea jonon merkit vasemmalta alkaen.
—A.3.4 Binääriluvut
Yksi tärkeä informaation prosessoinnin muoto on laskenta. Laskenta tarkoittaa prosessia, jossa suoritetaan matemaattisia toimenpiteitä luvuille. Tällöin syötteenä otettu bittijono merkitsee jotakin lukua, tai useita lukuja. Luvut voidaan esittää bittijonoina usealla eri tavalla. Jos tarkoituksena on suorittaa laskentaa, niin tällöin on kätevintä esittää luvut binäärimuodossa, jolloin jokaista lukua 0,1,2,3,... vastaa tietty yksikäsitteinen bittijono. Esimerkiksi yhteenlasku binäärimuotoisille luvuille on helppoa ja tulemme myöhemmin tarkastelemaan yhteenlaskua suorittavaa laitetta. Kun bittijono edustaa lukua binäärimuodossa, niin voimme selvyyden vuoksi kirjoittaa sen oikeaan alalaitaan 2. Esimerkiksi vastaa lukua 42. Puhumme binääriluvusta jos luku on esitetty binäärimuodossa. Kun tavallisesti luvut on esitetty 10-kantaisessa muodossa numeroiden 0,1,2,..,9 avulla, esiintyy binääriluvussa vain numeroita 0 ja 1. Binäärimuoto onkin toiselta nimeltään 2-kantainen muoto. Merkintäjärjestelmä on samanlainen kuin tavanomaisessa 10-kantaisessa kirjoituksessa, eli numeron paikka merkkaa kantaluvun kerrannaisia. Nolla ja ykkönen ovat samat molemmissa muodoissa eli
Kaikki luvun kaksi kerrannaiset ovat binäärimuodossa yksinkertaisia, samaan tapaan kuin luvun kymmenen kerrannaiset (eli sata, tuhat jne) 10-kantaisessa lukujärjestelmässä. Siispä
Näissä kakkosen kerrannaisissa nollien lukumäärä kertoo sen, kuinka monta kertaa kakkonen on kerrottu. Esimerkiksi 16 on 2 2
2
2, joten luvun binäärimuodossa on neljä nollaa.
Tarkastellaan sitten lukuja, jotka eivät ole kakkosen monikertoja. Aivan kuten 10-kantainen luku voidaan purkaa muotoon
, saadaan luvun binäärimuotokin kantaluvun monikertojen yhteenlaskuna. Esimerkiksi
sillä
ja
,
ja
.
Luvut ovat binäärimuodossa :
Osaisitko jatkaa listaa tästä eteenpäin?
Pääsitkö perille siitä, miten luvun kahdesta eri esitystavasta päästään toiseen? Testaa ymmärrystäsi seuraavalla kysymyksellä.
VL: mitä nuo alaindeksit 0 ja 1? Ahaa, pisteitä, mutta ovat hämäävässä paikassa, oikeastaan turhia.
—Luvun muuttaminen eri kantamuotojen välillä on hauskaa. Tällä kurssilla emme kuitenkaan keskity tämän asian harjoitteluun sen enempää. Jatkossa voit aina tarvittaessa käyttää alla olevaa lukumuunninta, joka löytyy alta. Voit jo tässä kohtaa testata sen käyttöä.
A.4 Porttilaskenta
Perehdymme tässä jaksossa porttilaskentaan, joka on yksi malli laskennalle ja yleisemmin informaation prosessoinnille. Kurssin loppuosa pitää sisällään aikaisempaa enemmän harjoituksia. Porttilaskenta ja kvanttiporttilaskenta tulevat parhaiten tutuiksi kun kokeilet erilaisia asioita simulaattoreilla riittävästi.
A.4.1 Porttisimulaattori
Yksi tapa mallintaa informaation prosessointia on ajatella sitä peräkkäisten muutosten jonona, jossa nämä muutokset yksittäin ovat yksinkertaisia tai ainakin helposti mallinnettavissa. Kutsumme yksittäistä muutoksen aiheuttavaa laitetta portiksi. Nimitys kuvaa sitä, että fysikaaliset bitit kulkevat näistä laitteista läpi. Kukin portti muuttaa jollakin tavoin yhtä tai useampaa bittiä. Porttien varsinainen toteutus riippuu siitä, millaiseen fysikaaliseen systeemin bitit ovat kirjoitettu. Meille olennaista on porttilaskennan antama malli informaation prosessoinnille emmekä tässä kohtaa välitä sen fysikaalisesta toteutuksesta.
Käytämme seuraavissa kokeiluissa ja tehtävissä porttisimulaattoria. Simulaattorissa voit vaihdella syötettä (input). Syöte on bittijono, joka on simulaattorin vasemmassa laidassa. Oikeassa laidassa on mittaus. Jokaisen bitin arvo mitataan erikseen, ja kokonaisuudessaan ne muodostavat ulostulon (output). Tässä välissä tapahtuu informaation prosessointi. Prosessointi tapahtuu vaiheittain ja kutsumme näitä vaiheita askeleiksi. Jokaisen askeleen kohdalle voit asettaa portteja, jotka muuttavat bittien arvoja. Askeleita voi jäädä myös tyhjäksi ja silloin niiden kohdalla ei tapahdu mitään.
Kuten aikaisemmin sovimme, q merkkaa bittijonoa joka on koko syöte, ja esim. q[0] syötteen ensimmäistä bittiä. Porttisimulaattorissa puhuttaessa q[0] viittaa sekä kyseiseen bittiin että bitin arvoon. Tämä ei aiheuta meille sekaannusta.
Porttisimulaattori näyttää tältä:
Syötettä saat vaihdettua kunkin bitin kohdalla nollasta ykköseksi ja takaisin klikkaamalla laatikkoa. Poikkeus ovat sellaiset bitit, joiden laatikoiden reunat ovat vaaleita. Niiden arvoa et voi muuttaa.
Välillä kehotetaan laittamaan portteja peräkkäin. Tämä tarkoittaa, että ne vaikuttavat samaan bittiin (tai samoihin bitteihin) eri askeleiden kohdalla.
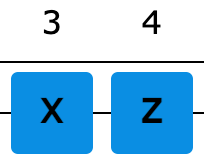
Käytössä olevat portit vaihtelevat eri tehtävissä. Simulaattorin käyttöohjeisiin (ympyröity kysymysmerkki simulaattorin oikealla laidalla) sinun ei tässä kohtaa tarvitse mennä, sillä harjoittelemme simulaattorin käyttöä vaiheittain. Tallenna -painikkeella raahaamasi portit jäävät muistiin. Se on myös merkki siitä, että olet suorittanut Kokeile itse -osion. Varsinaisissa tehtävissä tallentaminen saa aikaan tehtävän tarkistuksen ja pisteytyksen.
Mieti vielä videolla kuulemasi kuvaus porttilaskennasta ja vastaa seuraavaan kysymykseen.
A.4.2 X-portti
Eräs yhden bitin portti on X-portti. Pääset seuraavaksi selvittämään sen toiminnan itsenäisesti.
Please
Kokeile itse
Alla olevassa simulaattorissa voit raahata X-portin eri kohtiin ja muuttaa syötettä. Mitä X-portti tekee bitille? Miten voit kuvata sen toimintaa sanallisesti?
Expand by moving mouse over the exercise or by clicking
X-portti on hyvin yleinen portti ja sillä on käyttöyhteydestä riippuen useita nimiä. Eräs toinen tavallinen nimitys X-portille on NOT-portti. Tutki vielä edellisellä simulaattorilla sitä, miten kaksi peräkkäistä X-porttia tekee syötteelle ja vastaa sitten alla olevaan kysymykseen.
Tuntuuko helpolta vai tuottaako X-portti vaikeuksia? Katsotaan vielä yhteenveto X-portin toiminnasta videolta.
Kokeile vielä kolmeakin X-porttia peräkkäin. Vaihda syötettä ja vastaa alla olevaan kysymykseen.
Seuraavaksi saat eteesi ensimmäisen porttisimulaattoritehtävän. Tallenna-panikkeesta ratkaisuyrityksesi tarkistetaan. Jos se on väärin, niin voit kokeilla uudestaan. Yrityskertojen määrää ei ole rajoitettu.
Kvanttipöllön ohje
Porttitehtäviin yleinen ohje on: kokeile, kokeile ja kokeile. Kokeilemalla opit, miten eri portit toimivat. Oikea vastaus tehtävään alkaa hahmottua yritysten kautta. Pysähdy kuitenkin lopuksi miettimään, että miksi oikea vastaus on se mikä se on.
Please
Tehtävä
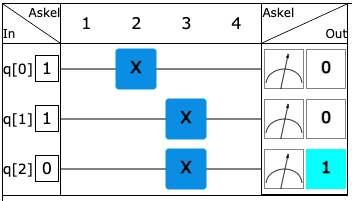
Käytä X-portteja siten, että syöte q=110 antaa ulostulon 101. Syöte ja ulostulo luetaan ylhäältä alas kohdista 'in' ja 'out'.
Expand by moving mouse over the exercise or by clicking
Tehdään vielä toinen samanlainen harjoitus.
Please
Tehtävä
Käytä X-portteja siten, että syöte q=101010 antaa ulostulon 100100.
Expand by moving mouse over the exercise or by clicking
Joidenkin tehtävien alla on Kvanttipöllön vinkki. Vinkkiä ei kannata katsoa heti, vaan yritä ensin tehdä tehtävä ilman sitä.
Yllä olevassa tehtävässä kannattaa ensimmäisenä laittaa syötteeksi q=101010. Laita sen jälkeen X-portteja siten, että ulostulo on halutunlainen.
A.4.3 Swap-portti
Portti voi vaikuttaa useampaan bittiin yhtä aikaa. Tällöin yksittäiselle bitille tapahtuva muutos voi riippua myös jonkin toisen bitin arvosta. Kahden bitin portit ovat olennaisia varsinkin laskennassa, sillä pelkästään yhden bitin porteilla syötteen bitit pysyvät erillisinä eikä niillä voi tehdä mitään kovinkaan hyödyllistä. Seuraavaksi pääset tutkimaan erään kahden bitin portin toimintaa.
Please
Kokeile itse
Raahaa kahden bitin portti haluamaasi paikkaan ja vaihtele syötteen arvoja. Mitä tämä portti tekee biteille? Miten voit kuvata sen toimintaa sanallisesti?
Expand by moving mouse over the exercise or by clicking
Yllä olevaa porttia kutsutaan swap-portiksi. Swap tarkoittaa vaihtamista, joten nimi on hyvin kuvaava tuolle portille. Sitä voisi kutsua myös vaihto-portiksi, mutta se nimitys ei ole vakiintunut. Swap-portin voisi myös kuvata siten, että reitit vaihtavat paikkaa. Eli näin:
Käytämme jatkossa rukseilla yhdistettyä viivaa kuvaamaan swap-porttia, sillä sitä on helppo siirrellä ja muokata. Huomasitko, että porttia voi venyttää sen jälkeen kun sen on laittanut paikalleen viemällä toisen pään kauemmaksi? Kokeile tätä ja tee alla oleva tehtävä. Muista, että syöte luetaan simulaattorissa ylhäältä alas.
Tutki sitten kahta peräkkäistä swap-porttia, jotka vaikuttavat samoihin bitteihin. Käytä yllä olevaa simulaattoria ja laita kaksi swap-porttia peräkkäin. Vaihtele syötteitä ja tarkastele, mikä on porttien kokonaisvaikutus.
Laita swap-portit eri askeleiden kohdalle. Vaikkapa askeleisiin 2 ja 3. Aseta portit siten, että molemmissa ylempi ruksi on bitin q[0] kohdalla ja alempi ruksi q[1] bitin kohdalla. 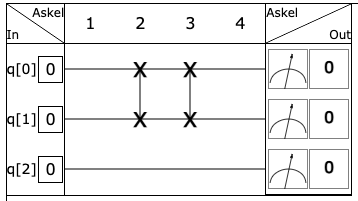 Nyt portit ovat peräkkäin ja vaikuttuvat samoihin bitteihin. Tutki porttien yhteisvaikutusta kokeilemalla läpi kaikki mahdolliset syötteet läpi.
Nyt portit ovat peräkkäin ja vaikuttuvat samoihin bitteihin. Tutki porttien yhteisvaikutusta kokeilemalla läpi kaikki mahdolliset syötteet läpi.
Mennään harjoittelussa eteenpäin. Seuraavassa tehtävässä kahdella erilaisella swap-portilla tarkoitetaan sitä, että ne eivät vaikuta täysin samoihin bitteihin. Kolmelle bitille on olemassa kolme erilaista swap-porttia ja ne näyttävät tältä:
Please
Tehtävä
Käytä kahta erilaista swap-porttia siten, että syöte q=100 antaa ulostulon 001 ja syöte q=001 ulostulon 010.
Expand by moving mouse over the exercise or by clicking
Nyt kun olemme tutustuneet kahteen eri porttiin, voimme raahata niitä porttisimulaattoriin sekaisin. Seuraavassa tehtävässä pääset eteenpäin, kun kokeilet erilaisia porttien yhdistelmiä ja siten etsit haluttua toimintoa.
Please
Tehtävä
Käytä X-portteja ja swap-porttia siten, että syöte q=00 antaa ulostulon 11, syöte q=11 ulostulon 00, ja kaksi muuta syötettä kulkevat läpi muuttumattomana.
Expand by moving mouse over the exercise or by clicking
Tehtävänantoon sisältyy olennainen vinkki porttien lukumäärästä: "..X-portteja ja swap-porttia..". Siispä riittää käyttää yhtä swap-porttia. Laita se vaikkapa askeleen 2 kohdalle, niin molemmin puolin mahtuu X-portteja. Sitten vaan kokeilet laittaa yksi, kaksi tai kolme X-porttia eri kohtiin. Vaihtelemalla syötettä voit testata yhdistelmän toimintaa.
A.4.4 CX-portti
Toinen kahden bitin portti on nimeltään control-X tai lyhyesti vain CX. Myös CNOT on tämän portin yksi lempinimistä, sillä muistanet X-portin olevan toiselta nimeltään NOT-portti.
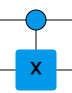
Aikaisemmin kokeilemamme swap-portti toimii symmetrisesti molempien bittien suhteen. Sen sijaan CX-portti ei ole toiminnaltaan symmetrinen, kuten sen symbolikin vihjaa. Tutki seuraavaksi CX-portin toimintaa.
Please
Kokeile itse
Tee alla olevassa simulaattorissa CX-portti yhdistämällä X-portti kontrollibittiin pallon avulla. Tutki sitten portin toimintaa vaihtelemalla syötettä. Miksi pallon kohdalla olevaa bittiä kutsutaan kontrollibitiksi?
Expand by moving mouse over the exercise or by clicking
Saitko CX-portin toiminnan selville? Kerrataan vielä, mistä siinä on kysymys.
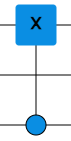
CX-portti koostuu kahdesta osasta, kontrollipallosta ja X-portista. Jos kontrollipalloon tulevan bitin arvo on 0, niin silloin X-portti ei vaikuta toiseen bittiin lainkaan. Jos taas kontrollibittiin tulee 1, niin X-portti toimii tavallisen X-portin tapaan. Kontrollipallo on siis ikään kuin kytkin, josta X-portin saa päälle tai pois.
Huomasitko, että CX-portissa kontrollipallon ei tarvitse olla X-porttia läheisimmällä bitillä?
Aikaisemmin kokeilemamme swap-portti toimii symmetrisesti molempien bittien suhteen. Sen sijaan CX-portti ei ole toiminnaltaan symmetrinen, kuten sen symbolikin vihjaa. Tutki seuraavaksi CX-portin toimintaa.
Voimme haluta kopioida bitin arvon useampaan toiseen bittiin. Kun yhden bitin arvo kopioidaan kahteen muuhun, on haluttu toiminta tällainen:
Huomaa, että emme välitä muista syötteistä kuin 000 ja 100, eli monistuksen kohteena olevat bitit ovat alkutilassa 0. Alkutila 0 vastaa tavalliseen kopiokoneeseen syötettävää tyhjää valkoista paperia.
Tarkastellaan bittikopiokoneen rakentamista seuraavassa tehtävässä.
Please
Tehtävä
Käytä kahta CX-porttia ja etsi niille sellainen muodostelma, että ensimmäisen bitin arvo q[0] kopioituu kahdelle seuraavalle bitille kun nämä ovat alkutilassa 0. Kun olet saanut piirin valmiiksi, paina 'Tallenna' ja ratkaisusi tarkistetaan.
Expand by moving mouse over the exercise or by clicking
Aikaisemmissa tehtävissä, jos tehtävän tekee oikein saa vastauksen correct (ainakin isossa osassa tehtäviä). Tämä tehtävä osaa kuitenkin jo suomea ja toteaa tehtävän olevan oikein :)
—Kuten tehtävänannossa sanottiin, tarkoituksena on käyttää kahta CX-porttia. Voit rauhassa kokeilla erilaisia vaihtoehtoja ja tutkia niiden toimintaa. Kopioinnissa ensimmäinen bitti määrää sen, mitä muille tapahtuu. Kuulostaako silloin luontevammalta laittaa sen kohdalla X-portti vai kontrollipallo? Kaksi alimmaista bittiä ovat samanlaisessa roolissa, joten niihin porttien pitää vaikuttaa samalla tavalla.
Edellisessä tehtävässä näimme, että kahden bitin portteja yhdistelemällä saadaan lopputulos, jossa kolmen bitin arvot kytkeytyvät keskenään. Tavallisesti tulemme toimeen yhden ja kahden bitin porteilla, joita laittamalla peräkkäin saadaan muodostettua useampaan bittiin vaikuttavia kokonaisuuksia. Joskus tulee käyttöön useammankin bitin portteja ja seuraavaksi tarkastelemme yhtä sellaista.
A.4.5 CCX-portti
Huomasitko, että X-porttiin voi liittää useamman kuin yhden pallon? Kun X-porttiin on yhdistetty kaksi kontrollipalloa, sanotaan porttia CCX-portiksi. Näin muodostetussa kokonaisuudessa X-portin ja kontrollipallojen pitää olla saman askeleen kohdalla. CCX-portti on siten kolmen bitin portti. Tälläkin portilla on useita lempinimiä, ja yksi niistä on Toffoli-portti. Tutki seuraavaksi tällaisen portin toimintaa.
Please
Kokeile itse
Tee alla olevassa simulaattorissa CCX-portti yhdistämällä X-porttiin kaksi kontrollibittiä. Tutki sitten portin toimintaa vaihtelemalla syötettä.
Expand by moving mouse over the exercise or by clicking
Kolmelle bitille voi tehdä kolme erilaista CCX-porttia. Nämä eroavat siitä, mitkä kaksi bittiä ovat kontrollibitteinä ja mihin taas vaikuttaa X-portti. Käytä seuraavan tehtävän tekemiseen yllä olevaa simulaattoria ja etsi joka kerralla oikeanlainen CCX-portti.
CCX-portti vaikuttaa kolmeen bittiin. Näistä yhteen tulee X-portti ja kahteen muuhun kontrollipallo. Erilaisia CCX-portteja on siten kolme ja ne näyttävät tältä: 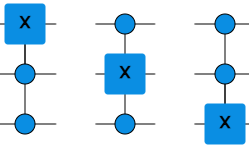
Seuraavassa tehtävässä sinun tulee kokeilla erilaisia CCX-porttien yhdistelmiä ja etsiä niistä sopiva.
Please
Tehtävä
Laita kaksi erilaista CCX-porttia peräkkäin siten, että syöte q=110 antaa ulostulon 111 ja syöte q=111 ulostulon 011.
Expand by moving mouse over the exercise or by clicking
Kaksi CCX-porttia peräkkäin voisi näyttää vaikkapa tältä: 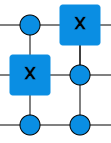 Kokeile tehtävänannon syötteitä tälle porttien yhdistelmälle. Jos ulostulo ei ole oikea, niin vaihda CCX-portteja.
Kokeile tehtävänannon syötteitä tälle porttien yhdistelmälle. Jos ulostulo ei ole oikea, niin vaihda CCX-portteja.
A.4.6 Piiri
Kun käytössä on useita bittejä ja monia portteja yhdistellään peräkkäin, kutsumme tätä kokonaisuutta piiriksi. Piirin toiminnassa meitä kiinnostaa se, miten erilaiset bittijonot muuttuvat piirin läpi kuljettuaan, eli mikä on ulostulo kaikilla mahdollisilla syötteillä. Kaksi eri piiriä, eli erilaista porttien yhdistelmää, voi johtaa samanlaiseen lopputulokseen. Tämä tarkoittaa, että ne antavat samat ulostulot kaikilla mahdollisilla syötteillä. Usein onkin tarkoituksenmukaista pyrkiä saamaan haluttu toiminta mahdollisimman pienellä määrällä portteja. Joskus jotkin muut seikat suosivat tiettyjen porttien käyttöä ylitse muiden. Jokin portti voi vaikkapa olla helpompi rakentaa kuin muut portit. Saattaa vaikkapa olla niin, että kahden bitin portteja voidaan toteutuksesta johtuen rakentaa ainoastaan lähimpien naapurien välille. Muut kahden bitin portit joudutaan silloin koostamaan näistä.
Porttilaskennassa piiri vastaa kokonaisprosessia. Jonkin tietyn informaatioprosessoinnin tehtävän suorittaminen saattaa vaatia lukuisia portteja, sillä portit yksinään ovat toiminnaltaan yksinkertaisia. Portteja voi olla piirissä paljon eikä niiden yhteisvaikutusta ole useinkaan helppo päätellä piiriä katsomalla. Porttisimulaattoritehtävissä kannattaa huoletta kokeilla annetun piirin toimintaa syötteitä vaihtelemalla, tai testata erilaisia porttiyhdistelmiä jos tehtävänäsi on rakentaa piiri.
Please
Kokeile itse
Tutki oheisen piirin toimintaa vaihtelemalla syötteitä. Mitä piiri tekee? Minkä bitin arvon muuttaminen vaikuttaa muihinkin bitteihin?
Expand by moving mouse over the exercise or by clicking
Yllä olevassa piirissä on neljä porttia, mutta sen toiminnan voi itse asiassa hoitaa jo pienemmällä määrällä portteja. Riitäisikö peräti yksi portti, vai tarvitaanko kaksi porttia?
Please
Tehtävä
Tee sellainen piiri, jolla on täsmälleen sama toiminta kuin yllä olevalla piirillä. Tämä tarkoittaa, että ulostulot ovat kaikilla syötteillä samat kuin ylläolevalla piirillä.
Expand by moving mouse over the exercise or by clicking
Sopivan piirin voi tehdä jo yhden portin avulla. Tarvitset siis ainoastaan yhden askeleen piirin tekemiseen. Kaikki tarjolla olevat portit ovat sinulle tuttuja, joten mene takaisin kokeilemaan annetun piirin toimintaa ja koita tunnistaa se. Huomasitko, että bitin q[1] arvon muuttaminen ei vaikuta muihin bitteihin eikä muiden muuttaminen siihen? Näin ollen kannattaa ensin kokeilla porttia, jossa q[1]:n kohdalle ei tule mitään. Bitit q[0] ja q[2] voit kytkeä toisiinsa joko swap-portilla tai CX-portilla. Kumpaa näistä annetun piirin toiminta muistuttaa?
Tehdään vielä toinen samanlainen harjoitus. Nyt piiri on monimutkaisempi. Pidä pää kylmänä ja testaa sen toimintaa. Piirin toiminta on yksinkertainen vaikkakin se koostuu kahdeksasta portista.
Please
Kokeile itse
Tutki oheisen piirin toimintaa vaihtelemalla syötteitä. Mitä piiri tekee?
Expand by moving mouse over the exercise or by clicking
Please
Tehtävä
Tee sellainen piiri, jolla on täsmälleen sama toiminta kuin yllä olevalla piirillä.
Expand by moving mouse over the exercise or by clicking
Kuten aikaisemmassa tehtävässä, tässäkin tapauksessa sopivan piirin voi tehdä jo yhden portin avulla. Testaa annettua piiriä riittävästi, että voit tunnistaa sen. Mitkä bitit siinä ovat sellaisia, että niiden muuttaminen ei vaikuta muihin eikä muiden muuttaminen niihin? Yksi biteistä taas on sellainen, että sen muuttaminen vaikuttaa myös johonkin toiseen bittiin. Nämä kaksi bittiä tulee silloin kytkeä toisiinsa sopivalla portilla.
Vaikka kahdessa piirissä olisi täysin samat portit, ei niiden toiminta välttämättä ole samanlainen. Lopputulokseen vaikuttaa nimittäin myös porttien järjestys. Tutkitaan tätä asiaa seuraavaksi. Rakennetaan kaksi piiriä allekkain, joissa on samat portit, mutta eri järjestyksessä.
Please
Kokeile itse
Kahteen ylimpään bittiin vaikuttaa swap ja CX peräkkäin. Laita kahteen alempaan bittiin nämä portit päinvastaiseen järjestykseen. Kokeile sitten erilaisia syötteitä, joissa näihin porttipareihin menee samanlaiset bittien arvot, eli q[0]=q[2] ja q[1]=q[3]. Onko porttien erilaisella järjestyksellä vaikutusta ulostuloon?
Expand by moving mouse over the exercise or by clicking
Kysymyksen tilanteessa on laitettu kaksi porttia peräkkäin, mutta eri järjestyksessä. Jos syötteeksi valitaan q=1010, niin silloin sekä ylempään että alempaan piiriin menee sama syöte 10. Ulostulosta nähdään, että nämä kaksi kahden bitin piiriä toimivat eri tavalla. Millä muilla syötteillä saat eri tulokset? Muista, että ylemmälle ja alemmalle piirille halutaan lähettää sama syöte, eli olemme kiinnostuneista syötteistä joilla q[0]=q[2] ja q[1]=q[3]. 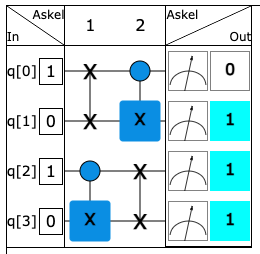
Kuten edellä näimme, porttien järjestyksellä on väliä: samat portit eri järjestykseen laitettuna saattavat muodostaa erilaiset piirit.
Kuten jo tämän jakson alussa näimme, kaksi hyvin erilaista piiriä saattaa antaa täysin saman ulostulon kaikilla syötteillä. Seuraavassa tehtävässä rakennetaan piiri, jolla on sama toiminta kuin swap-portilla, mutta piirissä on ainoastaan CX-portteja. Samaan lopputulokseen voidaan siis päästä käyttämällä jopa kokonaan eri portteja. Tämä tehtävä saattaa vaatia useampia kokeilukertoja. Ensin kannattaa kuitenkin kerrata swap-portin toiminta jaksosta A.4.3, että tiedät halutun lopputuloksen.
Please
Tehtävä
Tee usean CX-portin avulla piiri, jolla on sama toiminta kuin yksittäisellä swap-portilla. Kokeile erilaisia muodostelmia ja etsi sellainen, jossa kaikilla mahdollisilla syötteillä toiminta on halutunlainen.
Expand by moving mouse over the exercise or by clicking
Tehtävänannossa kehotaan käyttämään useaa CX-porttia. Kunkin CX-portin voit laittaa kahdella tavalla: joko kontrollipallo on ylhäällä tai alhaalla. Kuitenkin ainoastaan porttien keskinäinen asemointi halutun toiminnan kannalta on olennaista, sillä swap-portti toimii symmetrisesti. Näin ollen kaksi CX-porttia voi muodostaa piirin, jossa kontrollipallot ovat samalla puolella tai eri puolilla. Kokeile ensin nämä kaksi vaihtoehtoa läpi. Jos kumpikaan piiri ei toimi swap-portin tavoin, siirry käyttämään kolmea CX-porttia. Näissä joko kaikki kontrollipallot ovat samalla puolella tai sitten yksi on eri puolella kuin kaksi muuta. Erilainen CX-portti voi olla ensimmäisenä, keskellä tai viimeisenä. Näin ollen kolmen CX-portin piirejä on tehtävän kannalta neljä erilaista.
A.4.7 Virheenkorjaus
Kuvitellaan, että lähettelette ystäväsi Timin kanssa viestejä. Viestit ovat pitkiä bittijonoja, joihin on koodattu teille tärkeitä asioita. Viestinnässä on selvästi ollut jotain häikkää ja pian ymmärrätte, että viestintäkanavassa on häiriötä aiheuttavaa kohinaa. Kohina saa aikaiseksi sen, että joidenkin bittien arvo muuttuu lähetyksen ja vastaanoton välissä. Bittijono 1011101 esimerkiksi muuttuu muotoon 1001101. Siinä toisena olevan bitin arvo on vaihtunut. Arvon muuttuminen on melko harvinaista, mutta silti hyvin harmillista, sillä viestin sisältö saattaa silloin kokonaan muuttua. Tuleeko mieleesi keinoa, jolla voitte Timin kanssa taistella virheitä vastaan?
Yksi mahdollinen keino on lähettää jokainen bitti useampaan kertaan. Onhan sinulle ja Timille jo tuttu jaksossa A.4.4 läpikäyty CX-portin kyky kopioida bitin arvo moneksi, joten monistamisen voi automatisoida. Tuplana lähettäminen ei välttämättä hyödytä, sillä jos toinen bitin arvoista muuttuu, ei oikeaa arvoa voi tunnistaa. Triplana lähettämisestä sen sijaan on jo etua. Esimerkiksi bittijono 1011 lähetetään muodossa 111000111111. Yhden bitin arvon muuttuminen kussakin kolmen bitin ryppäässä kohinan vaikutuksesta ei haittaa, sillä vastaanottaja osaa silloin valita useimmin esiintyvän arvon kustakin kolmen ryppäästä. Koska oletamme arvon muuttumisen olevan harvinaista, on kahden bitin arvon muuttuminen samassa kolmen ryppäässä hyvin harvinaista. Tällainen harvinainen tapahtuma aiheuttaisi virheen viestinnässä.
VL: entä jos bittejä jää saamatta?
Kvanttipöllö: Hyvä kysymys! Siitä täytyykin tehdä erillinen tehtävä. Otetaan jatkokehittelyyn.
—
Tarvittaessa voidaan siirtyä käyttämään monistamista vieläkin useammaksi kuin kolmeksi. Seuraavassa tarkastelussa kuitenkin oletamme, että sinä ja Timi olette huomanneet triplaksi monistamisen riittävän.
Sinun ja Timin välinen virheitä sietävä viestintämenetelmä voidaan automatisoida. Bitin arvon monistaminen kolmeksi onnistuu jaksossa A.4.4 esitellyn kopiointipiirin avulla, ja niin onnistuu myös useimmin esiintyvän bitin arvon valinta. Alla oleva piiri tekee juuri tämän jälkimmäisen toiminnon: se valitsee syötteen kolmen ensimmäisen bitin arvoista yleisimmän.
Please
Kokeile itse
Tässä piirissä syöte on kolme ensimmäistä bittiä. Muut bitit ovat apubittejä ja niiden arvo on kiinnitetty nollaksi. Vaihtele syötettä. Tällöin kaikkien ulostulon bittien arvot muuttuvat. Yksi ulostulon biteistä on sellainen, joka kertoo yleisimmän syötteessä olleen arvon. Mikä on tämä ulostulo?
Expand by moving mouse over the exercise or by clicking
Syöte on kolme ensimmäistä bittiä, eli bitit q[0], q[1] ja q[2]. Piirin tarkoitus on poimia yleisin syötteen arvo. Jos esimerkiksi q[0]=0, q[1]=1 ja q[2]=0, niin silloin 0 esiintyy kaksi kertaa ja on yleisin arvo.
Kun vaihtelet syötteen arvoja, muuttuu ulostulon bitit. Jokin näistä ulostuloista antaa yleisimmän arvon. Kokeile riittävän monella eri syötteellä löytääksesi sen ulostulon, joka antaa yleisimmän arvon.
Edellinen yleisimmän bitin arvon valitseva piiri ei ole yksinkertainen. Timi koitti rakentaa piiriä, mutta muisti kytkennät väärin ja teki jotkin kohdat eri tavalla. Alla olevassa piirissä et voi muuttaa Timin jo sinne tekemiä portteja, mutta voit lisätä tyhjiin askeliin portteja. Sinun tulee täydentää piiri sellaiseksi, että sen toiminta vastaa aikaisempaa piiriä, eli se pystyy valitsemaan yleisimmän kolmen ensimmäisen bitin arvoista. Huomaa, että piiri ei voi ulkoisesti olla samanlainen Timin kytkemien porttien takia. Apubittien arvoilla ei ole väliä.
Please
Tehtävä
Täydennä piiri sellaiseksi, että se antaa bittien q[0], q[1] ja q[2] yleisimmän arvon samaan ulostulon bittiin kuin aikaisempi piiri.
Expand by moving mouse over the exercise or by clicking
Ihan aluksi vertaa annettua tekelettä aikaisempaan piiriin. Tästä voit jo tehdä päätelmiä sen suhteen, minkälaisia portteja annetusta piiristä puuttuu. Tuleeko tyhjiin askeliin X, CX vai CCX? Kun mietit aikaisempaa piiriä, niin siinä bitit q[0], q[1] ja q[2] ovat varsinaisia syötteitä. Lopuista viidestä bitistä yksi kertoo useiten esiintyvän bitin arvon ja neljä muuta ovat apubittien asemassa. Timin tekeleessä nämä apubitit ovat eri järjestyksessä kuin alkuperäisessä piirissä. Mieti siis apubittien osalta sitä, että mikä apubitti korvaa minkäkin. Tee sitten niin, että samassa roolissa oleville apubiteille tulee samanlaiset portit.
A.4.8 Yhteenlasku
Yksi tärkeimpiä informaation prosessoinnin toimintoja on yhteenlasku. Useat monimutkaisetkin laskut palautuvat lukujen yhteenlaskuun ja sitä kautta yhteenlaskua suorittava laite on hyödyllinen kapistus. On siis aika tarkastella yhteenlaskun suorittamista porttilaskennassa.
Binäärilukujen yhteenlasku on helppoa niin ihmiselle kuin tietokoneellekin. Olennaista on tietää seuraavien yksinkertaisten yhteenlaskujen tulokset. Tarvittaessa kertaa luvun binääriesitysmuoto jaksosta A.3.4 ja voit halutessasi muuttaa luvut 10-kantaisen muotoon voidaksesi valita oikeat vastaukset alla olevassa taulukossa.
Kaksi suurempaa binäärilukua voidaan laskea yhteen allekkain. Tällöin yhteenlasku palautuu yllä olevan taulukon yksinkertaisiin yhteenlaskuihin. Periaate on sama kuin 10-järjestelmän lukujen allekkainlaskussa, mutta metodi on helpompi sillä numeroita on vain kaksi.
Muistellaan ensin, miten 10-järjestelmässä lasketaan allekkain. Lasketaan yhteen luvut 219 ja 1822. Kirjoitamme luvut allekkain siten, että ykköset ovat samalla pystyrivillä, eli numerot 9 ja 2 osuvat kohdakkain. Viivan alle muodostuu laskun lopputulos.
219
+1822
----- Samalla pystyrivillä olevat numerot lasketaan yhteen ja toiminta etenee oikealta vasemmalle. Jos yhteenlaskun tulos on 10 tai enemmän, merkitään muistinumero 1 seuraavalle pystyriville.
1
219
+1822
-----
1 Näin jatketaan loppuun asti.
1 1
219
+1822
-----
2041 VL: eikö tässäkin kannattais merkitä 0-muistinumerot?
—Binäärilukujen allekkainlasku toimii samalla tavalla.
Binäärilukujen allekkainlasku on helppoa ja edellisten ohjeiden avulla osaisit laskea binäärilukuja yhteen paperin ja kynän avulla. Annetaan kuitenkin koneen hoitaa hommaa ja tarkastellaan seuraavaksi binääriyhteenlaskua suorittavaan simulaattoriin.
Jatkon kannalta on tärkeä ymmärtää muistirivin merkitys. Muistirivin takia allekkainlaskun toteuttamisessa tarvitaan kolmen bitin yhteenlaskua. Tuliko sinulle jo selväksi, mitä muistirivillä tarkoitetaan? Tee seuraava tehtävä yllä olevan laskukoneen avulla.
Mitä tämän tehtävän pitäisi opettaa? Se kyllä tarkistaa tekikö pyydetyn asian (kolme kertaa), mutta olisi kiva ymmärtää, minkä asian osaamista nyt testataan.
Kvanttipöllö: Tässä opetellaan muistirivin käsite. Se on olennainen myöhemmässä piirin avulla toteutetussa laskimessa.
VL: Tehtävä olisi ehkä mielekkäämpi jos ei tarvitsisi odottaa laskua loppuun, vaan voisi itse katsoa binäärilukuja, eli binääriluku ilmestyisi heti kun 10-järjestelmän lukua muuttaa.
—Koska yhteenlasku palautuu yksinkertaisiin summiin, riittää, että meillä on piiri joka laskee yhteen aikaisemman taulukon viisi helppoa summaa. Tätä piiriä toistuvasti käyttämällä voidaan sitten rakentaa laite, joka laskee pitkienkin binäärilukujen summan. Piirin täytyy ottaa kaksi bitin arvoa A ja B sekä mahdollisesti muistista kolmas bitin arvo, sillä allekkainlaskussa edellisestä summasta on voinut jäädä muistiin 1. Tällainen piiri on rakennettu alla.
Please
Kokeile itse
Alla olevassa piirissä on toteutettu kahden bitin A ja B binäärinen yhteenlasku siten, että mukaan voi tulla muistista myös kolmannen bitin arvo. Logiikkapiireissä kolmannesta bitistä puhutaan yleensä nimellä C (carry, muistinumero, muistibitti).</p> <p>Syötteessä kolmas bitti on edellisten bittien yhteenlaskusta tuleva muistibitti <span class="mathp inline"><img style="width:1.96347em; vertical-align:-0.23933em" src="data:image/svg+xml;base64,PD94bWwgdmVyc2lvbj0nMS4wJyBlbmNvZGluZz0nVVRGLTgnPz4KPCEtLSBUaGlzIGZpbGUgd2FzIGdlbmVyYXRlZCBieSBkdmlzdmdtIDIuMTQgLS0+CjxzdmcgdmVyc2lvbj0nMS4xJyB4bWxucz0naHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmcnIHhtbG5zOnhsaW5rPSdodHRwOi8vd3d3LnczLm9yZy8xOTk5L3hsaW5rJyB3aWR0aD0nMTYuMzYyMjI2cHQnIGhlaWdodD0nOS4zMDIxNjhwdCcgdmlld0JveD0nLS41MDAwMDIgLTcuMzA3Nzg2IDE2LjM2MjIyNiA5LjMwMjE2OCc+CjxkZWZzPgo8c3R5bGUgdHlwZT0ndGV4dC9jc3MnPgo8IVtDREFUQVtwYXRoIHtzdHJva2U6IGN1cnJlbnRDb2xvcjtzdHJva2Utd2lkdGg6IDAuMDVwdDt9XV0+Cjwvc3R5bGU+CjxwYXRoIGlkPSdnMS0xMDUnIGQ9J00yLjI1OTUyNy00LjM1ODY1NUMyLjI1OTUyNy00LjQ3MDIzNyAyLjE3NTg0MS00LjYyMzY2MSAxLjk4MDU3My00LjYyMzY2MUMxLjc5MjI3OS00LjYyMzY2MSAxLjU5MDAzNy00LjQ0MjM0MSAxLjU5MDAzNy00LjI0MDFDMS41OTAwMzctNC4xMjE1NDQgMS42ODA2OTctMy45NzUwOTMgMS44Njg5OTEtMy45NzUwOTNDMi4wNzEyMzMtMy45NzUwOTMgMi4yNTk1MjctNC4xNzAzNjEgMi4yNTk1MjctNC4zNTg2NTVaTS44MzY4NjItLjgxNTk0Qy44MDg5NjYtLjcyNTI4IC43NzQwOTctLjY0MTU5NCAuNzc0MDk3LS41MjMwMzlDLjc3NDA5Ny0uMTk1MjY4IDEuMDUzMDUxIC4wNjk3MzggMS40MzY2MTMgLjA2OTczOEMyLjEzMzk5OCAuMDY5NzM4IDIuNDQwODQ3LS44OTI2NTMgMi40NDA4NDctLjk5NzI2QzIuNDQwODQ3LTEuMDg3OTIgMi4zNTAxODctMS4wODc5MiAyLjMyOTI2NS0xLjA4NzkyQzIuMjMxNjMxLTEuMDg3OTIgMi4yMjQ2NTgtMS4wNDYwNzcgMi4xOTY3NjItLjk2OTM2NUMyLjAzNjM2NC0uNDExNDU3IDEuNzI5NTE0LS4xMjU1MjkgMS40NTc1MzQtLjEyNTUyOUMxLjMxODA1Ny0uMTI1NTI5IDEuMjgzMTg4LS4yMTYxODkgMS4yODMxODgtLjM2OTYxNEMxLjI4MzE4OC0uNTMwMDEyIDEuMzMyMDA1LS42NjI1MTYgMS4zOTQ3Ny0uODE1OTRDMS40NjQ1MDgtMS4wMDQyMzQgMS41NDEyMi0xLjE5MjUyOCAxLjYxNzkzMy0xLjM3Mzg0OEMxLjY4MDY5Ny0xLjU0MTIyIDEuOTMxNzU2LTIuMTc1ODQxIDEuOTU5NjUxLTIuMjU5NTI3QzEuOTgwNTczLTIuMzI5MjY1IDIuMDAxNDk0LTIuNDEyOTUxIDIuMDAxNDk0LTIuNDgyNjlDMi4wMDE0OTQtMi44MTA0NjEgMS43MjI1NC0zLjA3NTQ2NyAxLjMzODk3OS0zLjA3NTQ2N0MuNjQ4NTY4LTMuMDc1NDY3IC4zMjc3NzEtMi4xMjcwMjQgLjMyNzc3MS0yLjAwODQ2OEMuMzI3NzcxLTEuOTE3ODA4IC40MjU0MDUtMS45MTc4MDggLjQ0NjMyNi0xLjkxNzgwOEMuNTQzOTYtMS45MTc4MDggLjU1MDkzNC0xLjk1MjY3NyAuNTcxODU2LTIuMDI5MzlDLjc1MzE3Ni0yLjYyOTE0MSAxLjA2MDAyNS0yLjg4MDE5OSAxLjMxODA1Ny0yLjg4MDE5OUMxLjQyOTYzOS0yLjg4MDE5OSAxLjQ5MjQwMy0yLjgyNDQwOCAxLjQ5MjQwMy0yLjYzNjExNUMxLjQ5MjQwMy0yLjQ3NTcxNiAxLjQ1MDU2LTIuMzcxMTA4IDEuMjc2MjE0LTEuOTM4NzNMLjgzNjg2Mi0uODE1OTRaJy8+CjxwYXRoIGlkPSdnMS0xMTAnIGQ9J00uODUwODA5LS40MzkzNTJDLjgyMjkxNC0uMzQ4NjkyIC43ODEwNzEtLjE3NDM0NiAuNzgxMDcxLS4xNTM0MjVDLjc4MTA3MSAwIC45MDY2IC4wNjk3MzggMS4wMTgxODIgLjA2OTczOEMxLjE0MzcxMSAuMDY5NzM4IDEuMjU1MjkzLS4wMjA5MjIgMS4yOTAxNjItLjA4MzY4NlMxLjM4MDgyMi0uMzY5NjE0IDEuNDE1NjkxLS41MTYwNjVDMS40NTA1Ni0uNjQ4NTY4IDEuNTI3MjczLS45NjkzNjUgMS41NjkxMTYtMS4xNDM3MTFDMS42MTA5NTktMS4yOTcxMzYgMS42NTI4MDItMS40NTA1NiAxLjY4NzY3MS0xLjYxMDk1OUMxLjc2NDM4NC0xLjg5Njg4NyAxLjc3ODMzMS0xLjk1MjY3NyAxLjk4MDU3My0yLjIzODYwNUMyLjE3NTg0MS0yLjUxNzU1OSAyLjUwMzYxMS0yLjg4MDE5OSAzLjAyNjY1LTIuODgwMTk5QzMuNDMxMTMzLTIuODgwMTk5IDMuNDM4MTA3LTIuNTI0NTMzIDMuNDM4MTA3LTIuMzkyMDNDMy40MzgxMDctMS45NzM1OTkgMy4xMzgyMzItMS4xOTk1MDIgMy4wMjY2NS0uOTA2NkMyLjk0OTkzOC0uNzExMzMzIDIuOTIyMDQyLS42NDg1NjggMi45MjIwNDItLjUzMDAxMkMyLjkyMjA0Mi0uMTYwMzk5IDMuMjI4ODkyIC4wNjk3MzggMy41ODQ1NTggLjA2OTczOEM0LjI4MTk0MyAuMDY5NzM4IDQuNTg4NzkyLS44OTI2NTMgNC41ODg3OTItLjk5NzI2QzQuNTg4NzkyLTEuMDg3OTIgNC40OTgxMzItMS4wODc5MiA0LjQ3NzIxLTEuMDg3OTJDNC4zNzk1NzctMS4wODc5MiA0LjM3MjYwMy0xLjA0NjA3NyA0LjM0NDcwNy0uOTY5MzY1QzQuMTg0MzA5LS40MTE0NTcgMy44ODQ0MzMtLjEyNTUyOSAzLjYwNTQ3OS0uMTI1NTI5QzMuNDU5MDI5LS4xMjU1MjkgMy40MzExMzMtLjIyMzE2MyAzLjQzMTEzMy0uMzY5NjE0QzMuNDMxMTMzLS41MzAwMTIgMy40NjYwMDItLjYyMDY3MiAzLjU5MTUzMi0uOTM0NDk2QzMuNjc1MjE4LTEuMTUwNjg1IDMuOTYxMTQ2LTEuODg5OTEzIDMuOTYxMTQ2LTIuMjgwNDQ4QzMuOTYxMTQ2LTIuOTU2OTEyIDMuNDI0MTU5LTMuMDc1NDY3IDMuMDU0NTQ1LTMuMDc1NDY3QzIuNDc1NzE2LTMuMDc1NDY3IDIuMDg1MTgxLTIuNzE5ODAxIDEuODc1OTY1LTIuNDQwODQ3QzEuODI3MTQ4LTIuOTIyMDQyIDEuNDE1NjkxLTMuMDc1NDY3IDEuMTI5NzYzLTMuMDc1NDY3Qy44Mjk4ODgtMy4wNzU0NjcgLjY2OTQ4OS0yLjg1OTI3OCAuNTc4ODI5LTIuNjk4ODc5Qy40MjU0MDUtMi40NDA4NDcgLjMyNzc3MS0yLjA0MzMzNyAuMzI3NzcxLTIuMDA4NDY4Qy4zMjc3NzEtMS45MTc4MDggLjQyNTQwNS0xLjkxNzgwOCAuNDQ2MzI2LTEuOTE3ODA4Qy41NDM5Ni0xLjkxNzgwOCAuNTUwOTM0LTEuOTM4NzMgLjU5OTc1MS0yLjEyNzAyNEMuNzA0MzU5LTIuNTM4NDgxIC44MzY4NjItMi44ODAxOTkgMS4xMDg4NDItMi44ODAxOTlDMS4yOTAxNjItMi44ODAxOTkgMS4zMzg5NzktMi43MjY3NzUgMS4zMzg5NzktMi41Mzg0ODFDMS4zMzg5NzktMi40MDU5NzggMS4yNzYyMTQtMi4xNDc5NDUgMS4yMjczOTctMS45NTk2NTFTMS4xMDg4NDItMS40ODU0MyAxLjA3Mzk3My0xLjMzMjAwNUwuODUwODA5LS40MzkzNTJaJy8+CjxwYXRoIGlkPSdnMC02NycgZD0nTTcuNTcxNjA2LTYuOTI0MDM1QzcuNTcxNjA2LTYuOTUzOTIzIDcuNTUxNjgxLTcuMDIzNjYxIDcuNDYyMDE3LTcuMDIzNjYxQzcuNDMyMTMtNy4wMjM2NjEgNy40MjIxNjctNy4wMTM2OTkgNy4zMTI1NzgtNi45MDQxMUw2LjYxNTE5My02LjEzNjk4NkM2LjUyNTUyOS02LjI3NjQ2MyA2LjA2NzI0OC03LjAyMzY2MSA0Ljk2MTM5NS03LjAyMzY2MUMyLjczOTcyNi03LjAyMzY2MSAuNDk4MTMyLTQuODIxOTE4IC40OTgxMzItMi41MTA1ODVDLjQ5ODEzMi0uODY2NzUgMS42NzM3MjQgLjIxOTE3OCAzLjE5ODAwNyAuMjE5MTc4QzQuMDY0NzU3IC4yMTkxNzggNC44MjE5MTgtLjE3OTMyOCA1LjM0OTkzOC0uNjM3NjA5QzYuMjc2NDYzLTEuNDU0NTQ1IDYuNDQ1ODI4LTIuMzYxMTQ2IDYuNDQ1ODI4LTIuMzkxMDM0QzYuNDQ1ODI4LTIuNDkwNjYgNi4zNDYyMDItMi40OTA2NiA2LjMyNjI3Ni0yLjQ5MDY2QzYuMjY2NTAxLTIuNDkwNjYgNi4yMTY2ODctMi40NzA3MzUgNi4xOTY3NjItMi4zOTEwMzRDNi4xMDcwOTgtMi4xMDIxMTcgNS44Nzc5NTgtMS4zOTQ3NyA1LjE5MDUzNS0uODE2OTM2QzQuNTAzMTEzLS4yNTkwMjkgMy44NzU0NjctLjA4OTY2NCAzLjM1NzQxLS4wODk2NjRDMi40NjA3NzItLjA4OTY2NCAxLjQwNDczMi0uNjA3NzIxIDEuNDA0NzMyLTIuMTYxODkzQzEuNDA0NzMyLTIuNzI5NzYzIDEuNjEzOTQ4LTQuMzQzNzExIDIuNjEwMjEyLTUuNTA5MzRDMy4yMTc5MzMtNi4yMTY2ODcgNC4xNTQ0MjEtNi43MTQ4MTkgNS4wNDEwOTYtNi43MTQ4MTlDNi4wNTcyODUtNi43MTQ4MTkgNi42NDUwODEtNS45NDc2OTYgNi42NDUwODEtNC43OTIwM0M2LjY0NTA4MS00LjM5MzUyNCA2LjYxNTE5My00LjM4MzU2MiA2LjYxNTE5My00LjI4MzkzNVM2LjcyNDc4Mi00LjE4NDMwOSA2Ljc2NDYzMy00LjE4NDMwOUM2Ljg5NDE0Ny00LjE4NDMwOSA2Ljg5NDE0Ny00LjIwNDIzNCA2Ljk0Mzk2LTQuMzgzNTYyTDcuNTcxNjA2LTYuOTI0MDM1WicvPgo8L2RlZnM+CjxnIGlkPSdwYWdlMSc+Cjx1c2UgeD0nMCcgeT0nMCcgeGxpbms6aHJlZj0nI2cwLTY3Jy8+Cjx1c2UgeD0nNy4xMjA1MTUnIHk9JzEuNDk0MzgxJyB4bGluazpocmVmPScjZzEtMTA1Jy8+Cjx1c2UgeD0nOS45MzkyNDInIHk9JzEuNDk0MzgxJyB4bGluazpocmVmPScjZzEtMTEwJy8+CjwvZz4KPC9zdmc+" title="C_{in}"></span> ja seuraavien bittien yhteenlaskuun menevä muistibitti on ulostulossa nimellä <span class="mathp inline"><img style="width:2.43253em; vertical-align:-0.23933em" src="data:image/svg+xml;base64,PD94bWwgdmVyc2lvbj0nMS4wJyBlbmNvZGluZz0nVVRGLTgnPz4KPCEtLSBUaGlzIGZpbGUgd2FzIGdlbmVyYXRlZCBieSBkdmlzdmdtIDIuMTQgLS0+CjxzdmcgdmVyc2lvbj0nMS4xJyB4bWxucz0naHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmcnIHhtbG5zOnhsaW5rPSdodHRwOi8vd3d3LnczLm9yZy8xOTk5L3hsaW5rJyB3aWR0aD0nMjAuMjcxMDc1cHQnIGhlaWdodD0nOS4zMDIxNjhwdCcgdmlld0JveD0nLS41MDAwMDIgLTcuMzA3Nzg2IDIwLjI3MTA3NSA5LjMwMjE2OCc+CjxkZWZzPgo8c3R5bGUgdHlwZT0ndGV4dC9jc3MnPgo8IVtDREFUQVtwYXRoIHtzdHJva2U6IGN1cnJlbnRDb2xvcjtzdHJva2Utd2lkdGg6IDAuMDVwdDt9XV0+Cjwvc3R5bGU+CjxwYXRoIGlkPSdnMS0xMTEnIGQ9J00zLjcwMzExMy0xLjg1NTA0NEMzLjcwMzExMy0yLjYyOTE0MSAzLjEyNDI4NC0zLjA3NTQ2NyAyLjQ0MDg0Ny0zLjA3NTQ2N0MxLjQwODcxNy0zLjA3NTQ2NyAuNDMyMzc5LTIuMTA2MTAyIC40MzIzNzktMS4xNTA2ODVDLjQzMjM3OS0uNDUzMyAuOTQxNDY5IC4wNjk3MzggMS43MDE2MTkgLjA2OTczOEMyLjY5ODg3OSAuMDY5NzM4IDMuNzAzMTEzLS44NTA4MDkgMy43MDMxMTMtMS44NTUwNDRaTTEuNzA4NTkzLS4xMjU1MjlDMS4zNTk5LS4xMjU1MjkgMS4wMTEyMDgtLjM0ODY5MiAxLjAxMTIwOC0uODk5NjI2QzEuMDExMjA4LTEuMTg1NTU0IDEuMTQzNzExLTEuODY4OTkxIDEuNDE1NjkxLTIuMjY2NTAxQzEuNzE1NTY3LTIuNjk4ODc5IDIuMTIwMDUtMi44ODAxOTkgMi40MzM4NzMtMi44ODAxOTlDMi44MTA0NjEtMi44ODAxOTkgMy4xMzEyNTgtMi42MjIxNjcgMy4xMzEyNTgtMi4xMDYxMDJDMy4xMzEyNTgtMS45Mzg3MyAzLjA0NzU3Mi0xLjI0ODMxOSAyLjc0MDcyMi0uNzYwMTQ5QzIuNDc1NzE2LS4zNDg2OTIgMi4wNTcyODUtLjEyNTUyOSAxLjcwODU5My0uMTI1NTI5WicvPgo8cGF0aCBpZD0nZzEtMTE2JyBkPSdNMS43MTU1NjctMi43NTQ2N0gyLjQyNjg5OUMyLjU1OTQwMi0yLjc1NDY3IDIuNjUwMDYyLTIuNzU0NjcgMi42NTAwNjItMi45MDgwOTVDMi42NTAwNjItMy4wMDU3MjkgMi41NTk0MDItMy4wMDU3MjkgMi40NDA4NDctMy4wMDU3MjlIMS43NzgzMzFMMi4wMzYzNjQtNC4wMzc4NThDMi4wNDMzMzctNC4wNzI3MjcgMi4wNTcyODUtNC4xMDc1OTcgMi4wNTcyODUtNC4xMzU0OTJDMi4wNTcyODUtNC4yNjEwMjEgMS45NTk2NTEtNC4zNTg2NTUgMS44MjAxNzQtNC4zNTg2NTVDMS42NDU4MjgtNC4zNTg2NTUgMS41NDEyMi00LjI0MDEgMS40OTI0MDMtNC4wNTg3OEMxLjQ0MzU4Ny0zLjg4NDQzMyAxLjUzNDI0Ny00LjIxOTE3OCAxLjIyNzM5Ny0zLjAwNTcyOUguNTE2MDY1Qy4zODM1NjItMy4wMDU3MjkgLjI5MjkwMi0zLjAwNTcyOSAuMjkyOTAyLTIuODUyMzA0Qy4yOTI5MDItMi43NTQ2NyAuMzc2NTg4LTIuNzU0NjcgLjUwMjExNy0yLjc1NDY3SDEuMTY0NjMzTC43NTMxNzYtMS4xMDg4NDJDLjcxMTMzMy0uOTM0NDk2IC42NDg1NjgtLjY4MzQzNyAuNjQ4NTY4LS41OTI3NzdDLjY0ODU2OC0uMTgxMzIgLjk5NzI2IC4wNjk3MzggMS4zOTQ3NyAuMDY5NzM4QzIuMTY4ODY3IC4wNjk3MzggMi42MDgyMTktLjkwNjYgMi42MDgyMTktLjk5NzI2UzIuNTE3NTU5LTEuMDg3OTIgMi40OTY2MzgtMS4wODc5MkMyLjQxMjk1MS0xLjA4NzkyIDIuNDA1OTc4LTEuMDczOTczIDIuMzUwMTg3LS45NTU0MTdDMi4xNTQ5MTktLjUxNjA2NSAxLjc5OTI1My0uMTI1NTI5IDEuNDE1NjkxLS4xMjU1MjlDMS4yNjkyNC0uMTI1NTI5IDEuMTcxNjA2LS4yMTYxODkgMS4xNzE2MDYtLjQ2NzI0OEMxLjE3MTYwNi0uNTM2OTg2IDEuMTk5NTAyLS42ODM0MzcgMS4yMTM0NS0uNzUzMTc2TDEuNzE1NTY3LTIuNzU0NjdaJy8+CjxwYXRoIGlkPSdnMS0xMTcnIGQ9J00yLjk0OTkzOC0xLjEyOTc2M0MyLjkxNTA2OC0uOTkwMjg2IDIuODUyMzA0LS43MjUyOCAyLjgzODM1Ni0uNzE4MzA2QzIuNzA1ODUzLS41MDIxMTcgMi40MjY4OTktLjEyNTUyOSAxLjk5NDUyMS0uMTI1NTI5QzEuNTEzMzI1LS4xMjU1MjkgMS41MTMzMjUtLjU3ODgyOSAxLjUxMzMyNS0uNzA0MzU5QzEuNTEzMzI1LTEuMTE1ODE2IDEuNzA4NTkzLTEuNjEwOTU5IDEuOTAzODYxLTIuMTIwMDVDMS45NTk2NTEtMi4yNTk1MjcgMi4wMDE0OTQtMi4zNjQxMzQgMi4wMDE0OTQtMi40NzU3MTZDMi4wMDE0OTQtMi44MzgzNTYgMS42OTQ2NDUtMy4wNzU0NjcgMS4zMzg5NzktMy4wNzU0NjdDLjY0MTU5NC0zLjA3NTQ2NyAuMzI3NzcxLTIuMTIwMDUgLjMyNzc3MS0yLjAwODQ2OEMuMzI3NzcxLTEuOTE3ODA4IC40MjU0MDUtMS45MTc4MDggLjQ0NjMyNi0xLjkxNzgwOEMuNTQzOTYtMS45MTc4MDggLjU1MDkzNC0xLjk1MjY3NyAuNTcxODU2LTIuMDI5MzlDLjczOTIyOC0yLjYwMTI0NSAxLjA0NjA3Ny0yLjg4MDE5OSAxLjMxODA1Ny0yLjg4MDE5OUMxLjQzNjYxMy0yLjg4MDE5OSAxLjQ5MjQwMy0yLjgwMzQ4NyAxLjQ5MjQwMy0yLjYzNjExNUMxLjQ5MjQwMy0yLjQ3NTcxNiAxLjQzNjYxMy0yLjMyOTI2NSAxLjM2Njg3NC0yLjE2ODg2N0MuOTkwMjg2LTEuMjA2NDc2IC45OTAyODYtMS4wMDQyMzQgLjk5MDI4Ni0uODE1OTRDLjk5MDI4Ni0uNjk3Mzg1IC45OTAyODYtLjM3NjU4OCAxLjI0ODMxOS0uMTUzNDI1QzEuNDUwNTYgLjAxMzk0OCAxLjcyMjU0IC4wNjk3MzggMS45NjY2MjUgLjA2OTczOEMyLjQwNTk3OCAuMDY5NzM4IDIuNjQzMDg4LS4xNjczNzIgMi44NzMyMjUtLjM5MDUzNUMzLjAyNjY1IC4wNTU3OTEgMy40OTM4OTggLjA2OTczOCAzLjU3NzU4NCAuMDY5NzM4QzMuODE0Njk1IC4wNjk3MzggMy45OTYwMTUtLjA2OTczOCA0LjEyODUxOC0uMjk5ODc1QzQuMjgxOTQzLS41NzE4NTYgNC4zNzk1NzctLjk3NjMzOSA0LjM3OTU3Ny0uOTk3MjZDNC4zNzk1NzctMS4wODc5MiA0LjI4MTk0My0xLjA4NzkyIDQuMjYxMDIxLTEuMDg3OTJDNC4xNjMzODctMS4wODc5MiA0LjE1NjQxMy0xLjA2MDAyNSA0LjEwNzU5Ny0uODcxNzMxQzQuMDIzOTEtLjU0Mzk2IDMuODkxNDA3LS4xMjU1MjkgMy41OTg1MDYtLjEyNTUyOUMzLjQxNzE4Ni0uMTI1NTI5IDMuMzY4MzY5LS4yODU5MjggMy4zNjgzNjktLjQ2NzI0OEMzLjM2ODM2OS0uNTg1ODAzIDMuNDI0MTU5LS44MzY4NjIgMy40NzI5NzYtMS4wMTgxODJDMy41MjE3OTMtMS4yMDY0NzYgMy41OTE1MzItMS40OTI0MDMgMy42MjY0MDEtMS42NDU4MjhMMy43ODY4LTIuMjY2NTAxQzMuODI4NjQzLTIuNDQwODQ3IDMuOTA1MzU1LTIuNzQ3Njk2IDMuOTA1MzU1LTIuNzgyNTY1QzMuOTA1MzU1LTIuOTIyMDQyIDMuNzkzNzczLTMuMDA1NzI5IDMuNjc1MjE4LTMuMDA1NzI5QzMuNDE3MTg2LTMuMDA1NzI5IDMuMzY4MzY5LTIuODAzNDg3IDMuMzEyNTc4LTIuNTgwMzI0TDIuOTQ5OTM4LTEuMTI5NzYzWicvPgo8cGF0aCBpZD0nZzAtNjcnIGQ9J003LjU3MTYwNi02LjkyNDAzNUM3LjU3MTYwNi02Ljk1MzkyMyA3LjU1MTY4MS03LjAyMzY2MSA3LjQ2MjAxNy03LjAyMzY2MUM3LjQzMjEzLTcuMDIzNjYxIDcuNDIyMTY3LTcuMDEzNjk5IDcuMzEyNTc4LTYuOTA0MTFMNi42MTUxOTMtNi4xMzY5ODZDNi41MjU1MjktNi4yNzY0NjMgNi4wNjcyNDgtNy4wMjM2NjEgNC45NjEzOTUtNy4wMjM2NjFDMi43Mzk3MjYtNy4wMjM2NjEgLjQ5ODEzMi00LjgyMTkxOCAuNDk4MTMyLTIuNTEwNTg1Qy40OTgxMzItLjg2Njc1IDEuNjczNzI0IC4yMTkxNzggMy4xOTgwMDcgLjIxOTE3OEM0LjA2NDc1NyAuMjE5MTc4IDQuODIxOTE4LS4xNzkzMjggNS4zNDk5MzgtLjYzNzYwOUM2LjI3NjQ2My0xLjQ1NDU0NSA2LjQ0NTgyOC0yLjM2MTE0NiA2LjQ0NTgyOC0yLjM5MTAzNEM2LjQ0NTgyOC0yLjQ5MDY2IDYuMzQ2MjAyLTIuNDkwNjYgNi4zMjYyNzYtMi40OTA2NkM2LjI2NjUwMS0yLjQ5MDY2IDYuMjE2Njg3LTIuNDcwNzM1IDYuMTk2NzYyLTIuMzkxMDM0QzYuMTA3MDk4LTIuMTAyMTE3IDUuODc3OTU4LTEuMzk0NzcgNS4xOTA1MzUtLjgxNjkzNkM0LjUwMzExMy0uMjU5MDI5IDMuODc1NDY3LS4wODk2NjQgMy4zNTc0MS0uMDg5NjY0QzIuNDYwNzcyLS4wODk2NjQgMS40MDQ3MzItLjYwNzcyMSAxLjQwNDczMi0yLjE2MTg5M0MxLjQwNDczMi0yLjcyOTc2MyAxLjYxMzk0OC00LjM0MzcxMSAyLjYxMDIxMi01LjUwOTM0QzMuMjE3OTMzLTYuMjE2Njg3IDQuMTU0NDIxLTYuNzE0ODE5IDUuMDQxMDk2LTYuNzE0ODE5QzYuMDU3Mjg1LTYuNzE0ODE5IDYuNjQ1MDgxLTUuOTQ3Njk2IDYuNjQ1MDgxLTQuNzkyMDNDNi42NDUwODEtNC4zOTM1MjQgNi42MTUxOTMtNC4zODM1NjIgNi42MTUxOTMtNC4yODM5MzVTNi43MjQ3ODItNC4xODQzMDkgNi43NjQ2MzMtNC4xODQzMDlDNi44OTQxNDctNC4xODQzMDkgNi44OTQxNDctNC4yMDQyMzQgNi45NDM5Ni00LjM4MzU2Mkw3LjU3MTYwNi02LjkyNDAzNVonLz4KPC9kZWZzPgo8ZyBpZD0ncGFnZTEnPgo8dXNlIHg9JzAnIHk9JzAnIHhsaW5rOmhyZWY9JyNnMC02NycvPgo8dXNlIHg9JzcuMTIwNTE1JyB5PScxLjQ5NDM4MScgeGxpbms6aHJlZj0nI2cxLTExMScvPgo8dXNlIHg9JzExLjA1MzAwMScgeT0nMS40OTQzODEnIHhsaW5rOmhyZWY9JyNnMS0xMTcnLz4KPHVzZSB4PScxNS43NjMzOTYnIHk9JzEuNDk0MzgxJyB4bGluazpocmVmPScjZzEtMTE2Jy8+CjwvZz4KPC9zdmc+" title="C_{out}"></span>. Tutki piirin toimintaa vaihtelemalla kolmen ensimmäisen bitin arvoja ja varmistu, että piiri toimii toivotulla tavalla. Ulostulossa S on summan viimeisin bitti, eli se joka allekkain laskussa tulee viivan alle.
Expand by moving mouse over the exercise or by clicking
Tehtävänannon tekstiä voisi hieman täsmentää. Ekassa lauseessa puhutaan C:stä, mutta tämän nimistä syötettä ei ole (merkitys kyllä selviää, mutta ohjelmoitaessa muuttujien nimillä on merkitys). Lisäksi voisi kertoa, että muuttujien nimeämisen taustalla on logiikkapiireistä tyypillinen käytäntö (C_in = Carry in, C_out = Carry out)
—Jäikö piirin yhteys allekkainlaskuun epäselväksi? Katsotaan asiaa vielä esimerkin avulla.
Lasketaan yhteen luvut 39 ja 22. Binäärilukuina nämä ovat 100111 ja 10110. Laitetaan ne ensin allekkain.
Ensimmäisessä vaiheessa lasketaan oikean puoleisin pystyrivi. Kun tähän käytetään yllä olevaa piiriä, niin syötteeksi valitaan A=1 ja B=0. Ensimmäisessä laskussa ei muistissa voi vielä olla mitään, joten Cin=0. Koska 1+0 = 1, niin S=1 ja Cout=0.
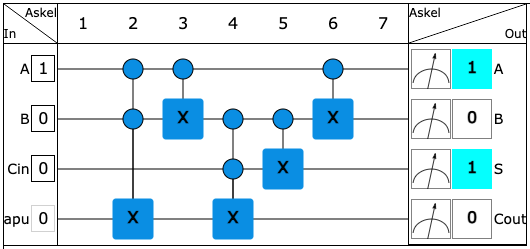
Merkitään S viivan alle ja Cout muistiin:
Seuraavassa vaiheessa piirin syöte on A=1, B=1 ja Cin=0. Sillä 1+1=10, niin S=0 ja Cout=1.
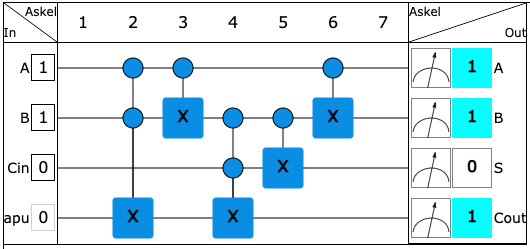
Merkitään taas S viivan alle ja Cout muistiin:
Seuraavassa vaiheessa A=1, B=1 ja Cin=1. Sillä 1+1+1=11, niin S=1 ja Cout=1.
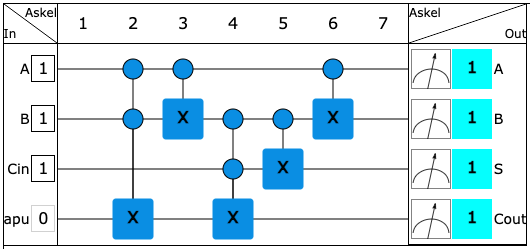
Merkitään S viivan alle ja Cout muistiin:
Näin lasku etenee. Jokaisen pystyrivin kohdalla piiriä käytetään kerran.
Yhteenlaskussa tavallisesti unohdetaan informaatiota siinä mielessä, että esim. 4+5 = 9, mutta lopputuloksesta 9 ei voi päätellä laskettiinko yhteen 4+5 vai vaikkapa 3+6. Yllä kuvattu piiri ei hukkaa informaatiota. Tämä tarkoittaa, että jokaisesta mahdollisesta ulostulosta voi yksikäsitteisesti päätellä syötteen. Syynä tähän on se, että pidämme ulostulossa mukana A:n ja B:n arvot. Pelkkää yhteenlaskun lopputulosta ajatellen ainoastaan summa ja Cout riittäisivät, sillä ainoastaan nämä tarvitaan allekkainlaskun seuraavassa vaiheessa. Lukuja voidaan kuitenkin haluta käyttää johonkin toiseen laskuun, joten niiden säilyttäminen on hyödyllistä.
Kahden bitin binäärinen yhteenlasku voidaan tehdä helpomminkin jos muistista ei tule kolmannen bitin arvoa eikä muistiin tarvitse jäädä syötettä muuttumattomana, kuten yllä. Tällainen yksinkertaisempi piiri voi suorittaa taulukon neljä ylintä riviä. Sitä ei kuitenkaan voida käyttää allekkainlaskussa, sillä viidennen rivin yhteenlasku ei onnistu. Kahden bitin binäärinen summa on joko 00, 01, 10, jossa yhtenäisyyden vuoksi merkitsemme kaikki nollat näkyviin. Seuraavassa tehtävässä S on tällainen kahdella bitillä merkattu summa. Jos esimerkiksi A=1, B=0, niin S=01 ja näin ollen S[0]=0 ja S[1]=1.
Please
Tehtävä
Rakenna piiri, joka toteuttaa kahden bitin A ja B yhteenlasku siten, että A menee läpi muuttumattona, S[0] on summan <strong>vasen</strong> bitti ja S[1] summan <strong>oikea</strong> bitti. Ota huomioon ulostulojen S[0] ja S[1] oikea järjestys. Simulaattorissa S[1] on keskimmäinen bitti ja S[0] alin bitti.
Expand by moving mouse over the exercise or by clicking
Otitko huomioon bittien S[0] ja S[1] oikean järjestyksen? Niiden ajatteleminen väärässä järjestyksessä on suurin syy ongelmiin.
Aikaisemmin tarkastelemamme piiri laskee kaksi bittiä yhteen ja hoitaa vieläpä muistista tulevan bitin yhteenlaskussa oikein. Tehtävässä pyydetään tekemään sellainen piiri, joka hoitaa vain osan tästä. Kannattaa kokeilla erilaisia palasia aikaisemmasta piiristä ja tutkia, mikä pala tekee halutun laskun. Muistipaikasta tulevaa bittiä C ei halutussa piirissä ole, joten se antaa osviittaa siitä mitkä portit aikaisemmasta piiristä voi pudottaa pois. Piirissä on tilaa kolmelle portille, mutta välttämättä et tarvitse niitä kaikkia.
Halutun piirin tulee toimia seuraavasti:
- A=0, B=0
summa on 0, joten S[0]=0, S[1]=0
- A=0, B=1
summa on 1, joten S[0]=0, S[1]=1
- A=1, B=0
summa on 1, joten S[0]=0, S[1]=1
- A=1, B=1
summa on 10, joten S[0]=1, S[1]=0
Kaikissa tapauksissa A:n arvon pitää menee läpi muuttumattomana. Esimerkiksi tilanteessa A=1, B=0 ulostulo näyttää tältä:
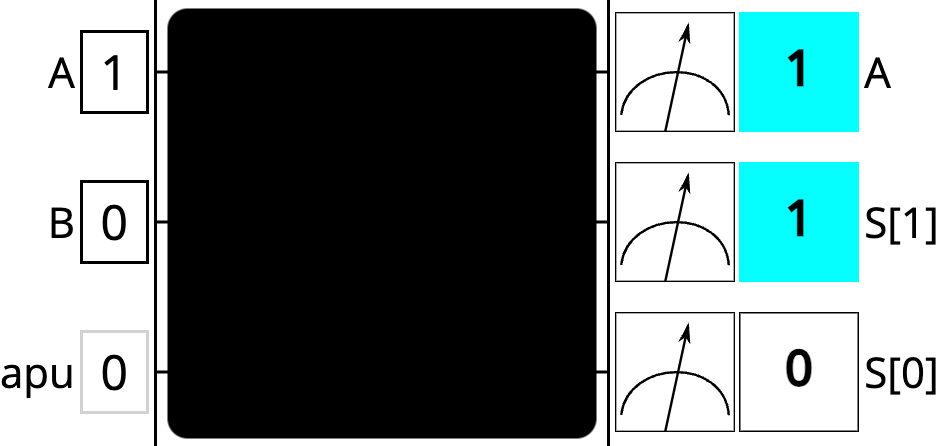
Sinun pitää etsiä sopiva piiri mustan laatikon paikalle ja kokeilla läpi kaikki mahdolliset syötteet.
A.5 Kvanttiporttilaskenta
Tässä jaksossa perehdymme porttilaskennan kvanttifysikaaliseen versioon, eli kvanttiporttilaskentaan.
A.5.1 Kvanttibitti eli kubitti
Aikaisemmin olemme todenneet, että informaatio ei voi esiintyä ilman fysikaalista systeemiä, vaan sillä täytyy olla fysikaalinen kantaja. Informaation kantajana voi olla myös kvanttifysikaalinen systeemi.
Aivan kuten muidenkin fysikaalisten systeemien tapauksessa, tapahtuu informaation kirjoittaminen kvanttisysteemiin preparoimalla se sopivalla tavalla. Vastaavasti informaation lukeminen tapahtuu siihen tarkoitukseen sopivalla mittauksella. Yksinkertaisimmalla mahdollisella kvanttisysteemillä on ainoastaan kaksi toisistaan täydellisesti eroteltavaa tilaa. Tällaista systeemiä kutsutaan kvanttibitiksi, eli kubitiksi.
Kubitilla on äärettömän paljon tiloja kaiken kaikkiaan, ja tämä erottaa sen olennaisella tavalla bitistä. Kubitti on bitin kaltainen informaation kantaja siinä mielessä, että jokaisella tilalla on tarkalleen yksi ortogonaalinen tila, eli toinen tila, jonka siitä pystyy täysin erottamaan. Näin ollen yhden kubitin avulla voi lähettää ainoastaan yhden bitin verran informaatiota. Kubittiin kirjoitettua informaatiota voidaan kuitenkin prosessoida kvanttifysikaalisilla operaatioilla, ja tämä tekee jo yhdestä kubitista erilaisen informaation kantajan kuin aikaisemmin näkemämme bitin fysikaaliset ilmentymät.
Kun valitaan kaksi kubitin ortogonaalista tilaa, voidaan niitä ajatella bittitiloina 0 ja 1. Prosessoinnissa nämä tilat voivat muuttua superpositiotiloiksi, jotka ovat yhdistelmiä tiloista 0 ja 1. Näissä superpositiotiloissa kubitilla ei ole määrättyä bitin arvoa, vaan mittauksessa saadaan satunnaisesti 0 tai 1. Täytyy vielä korostaa, että kubitti on jokaisena ajanhetkenä kuitenkin vain yhdessä tilassa. Tuon tilan ominaisuudet saattavat vain olla sellaiset, että siinä ilmenee jotakin 'nollamaista' ja jotakin 'ykkösmäistä'. Superpositiotilassa näitä kahta piirrettä voi olla eri painotuksilla, ja näin ollen erilaisia superpositiotiloja on äärettömän paljon.
Kaikki aikaisemmin läpikäymämme portit toimivat kubiteille. Jos kubitti on tilassa 0 tai 1, toimivat X-portti, CX-portti ja muut läpikäymämme portit aivan samalla tavoin kuin olemme oppineet bitin tapauksessa. Mutta silloin kun kubitti on superpositiotilassa, on porttien toiminta erilaista. Aikaisemmin jaksossa A.4.4 tarkastelimme kopiokonetta, jolla halutun bitin tila saadaan kopioitua yhteen tai useampaan bittiin. Kopiokone ei kuitenkaan monista superpositiotilaa kahdeksi samanlaiseksi superpositiotilaksi. Tämä onkin yksi suurin ero bitin ja kubitin välillä informaation prosessoinnin kannalta: bitin tuntemattoman tilan voi monistaa, mutta kubitin tuntematonta tilaa ei voi monistaa. Näin ollen myöskään jaksossa A.4.7 käsitelty virheenkorjaus ei toimi yhtä helposti kuin biteillä, vaan siihen pitää keksiä uudenlaiset keinot.
Superposition lisäksi kvanttisysteemeillä on toinen piirre, joka on olennainen kvantti-informaation prosessoinnissa. Useampi kubitti voi olla sellaisessa yhteisessä kvanttitilassa, jota ei voi kirjoittaa yksittäisten kubittitilojen yhdistelmänä. Tällöin kahden tai useamman kubitin tilat ovat keskenään lomittuneet ja niiden yhteistä tilaa sanotaan lomittuneeksi tilaksi. Lomittuminen on yksi niistä ilmiöistä, jotka tekevät kvanttifysikaalisista systeemeistä selvästi erilaisia kuin klassisen fysiikan kappaleet. Lomittumisella ei ole vastinetta klassisessa fysiikassa ja sen takia sen havainnollistaminen on hankalaa. Lomittumisen selittäminen onnistuu matematiikan avulla ja palaammekin asiaan Kvanttiaakkosten B-osassa, kun meillä on tarvittava matemaattinen koneisto käytössä.
Kubitti voidaan toteuttaa useilla eri kvanttifysikaalisilla tavoilla. Esimerkiksi yhteenkytketyistä suprajohtavista elektrodeista voidaan valmistaa erilaisia kubitin toteutuksia. Kun puhumme kubitistä emme viittaa mihinkään tiettyyn fysikaaliseen toteutukseen, vaan kuten bitinkin tapauksessa mihin hyvänsä kubitin toteuttavaan systeemiin.
Seuraavaksi siirrymme käyttämään kvanttiporttisimulaattoria. Kubitin ominaisuudet tulevat esille tehtäviä tehdessä. Varsinaiseen matemaattiseen kuvaukseen menemme vasta Kvanttiaakkosten B-osassa.
A.5.2 Kvanttiporttisimulaattori
Kvanttiporttilaskenta on periaatteeltaan samanlaista kuin porttilaskenta: informaatiota kantavalle systeemille tehdään muutoksia askeleittain ja lopuksi suoritetaan mittaus. Bittien sijaan kvanttiporttilaskennassa prosessoidaan kubitteja.
Käydään vielä läpi videon pääkohdat. Tavanomaisesti alkutilana kubitille käytetään joitakin valittuja ortogonaalisia tiloja, jotka vastaavat bittitiloja 0 ja 1. Merkitsemme syötteen arvot muodossa ja
muistutuksena siitä, että kyseessä on kvanttiporttilaskenta tavallisen porttilaskennan sijaan. Tämä merkintätapa on peräisin Paul Diracilta, yhdeltä kvanttimekaniikan pioneereista, ja se on jäänyt kvanttifyysikkojen käyttöön. Kvanttiaakkosten B-osassa tämän merkintätavan hyödyllisyys tulee paremmin esille, mutta otamme sen jo nyt käyttöön.
Kun laskenta aloitetaan, kubitit preparoidaan syötettä vastaaviin tiloihin. Prosessoinnin lopuksi suoritetaan mittaus, jonka ulostulona saadaan bittijono. Se, että mittausta ennen kubitit ovat superpositiotilassa, tulee esille siten, että mittauksen ulostulo on satunnainen. Kvanttimittauksen lopputulos onkin paras ymmärtää todennäköisyysjakaumana ja tästähän jo jaksossa A.2.4 puhuimmekin.
Kaikki aikaisemmin tutustumamme portit toimivat sellaisenaan kvanttiporttilaskennassa. Ne tosin eivät muuta alkutiloja superpositiotiloiksi. Siihen, että alkutila saadaan muutettua superpositiotilaksi tai lomittuneeksi tilaksi, tarvitaan kvanttiportteja. Kvanttiporttisimulaattorissa on mukana näitä kvanttiportteja, joita käymme läpi tässä jaksossa.
Käyttämämme kvanttiporttisimulaattori näyttää tältä:
Kvanttiporttilaskennan lopputulosta voimme kuvata eri tavoin. Yllä olevassa kuvassa on yksittäisiä mittauskertoja kuvaava taulukko. Myöhemmin tarkastelemme myös koko todennäköisyysjakaumaa.
A.5.3 H-portti
Aikaisemmin läpikäymämme X-portti toimii myös kubitille. Se, että kubitilla on ääretön määrä eri tiloja, mahdollistaa kubitin prosessoinnin tavalla, johon bitti ei sovellu. Yksinkertainen mutta tärkeä yhden kubitin portti on Hadamard-portti eli lyhyesti H-portti. Tällä portilla ei ole vastinetta tavalliselle bitille vaan se vaatii toimiakseen kubitin.
Please
Kokeile itse
Tutki alla olevalla kvanttiporttisimulaattorilla ensin meille jo tutun X-portin toimintaa ja sen jälkeen H-portin toimintaa. Tee molemmissa tapauksissa useita mittauksia eri syötteillä ja selvitä onko lopputulos aina samanlainen vai satunnainen. Satunnainen lopputulos tarkoittaa, että samalla syötteellä ulostulo voi vaihdella mittauskerrasta riippuen.
Expand by moving mouse over the exercise or by clicking
Kuten simulaattorilla voit todeta, H-portin tapauksessa mittaustulos vaihtelee mittauskerrasta riippuen. Syy tähän on se, että H-portti laittaa alkutilan tilojen ja
superpositiotilaan. Tässä superpositiotilassa kubitilla ei ole kiinnitettyä ominaisuutta olla joko 0 tai 1. Mittauksessa pakotamme jommankumman vaihtoehdon ulos. Se, tuleeko mittaustulokseksi 0 vai 1, on sattumaa.
Käytä vielä samaa kvanttiporttisimulaattoria ja kokeile kahden portin yhdistelmiä, eli laita kaksi porttia peräkkäin. Antavatko kahden portin yhdistelmät varmasti ennustettavan vai satunnaisen lopputuloksen?
Kvanttifysiikassa mittaustulos on useimmissa tilanteissa satunnainen ja ainoastaan erityistapauksissa jokin mittaustulos tapahtuu varmuudella. Tästä johtuen kvanttiporttien toiminta selviää vasta suorittamalla useita mittauksia ja kokoamalla näistä mittaustulostilaston. Kvanttipiirin toiminnan voi esittää todennäköisyyksien pylväsdiagrammin avulla, jota jaksossa A.2.4 harjoittelimmekin. Pylväsdiagrammissa valitulle syötteelle listataan kaikki ulostulot ja annetaan näiden todennäköisyydet. Jos jonkin ulostulon todennäköisyys on 100%, niin silloin tämä ulostulo saadaan mittauksessa joka kerta. Muutoin ulostulot tapahtuvat satunnaisesti todennäköisyysjakauman listauksen mukaisesti. Esitämme pylväsdiagrammin vaakatasossa kvanttiporttisimulaattorin alla. Lisäksi kunkin ulostulon kohdalla näet pylvään, joka kuvaa ulostulon 1 todennäköisyyttä.
Please
Kokeile itse
Tutki uudestaan H-portin toimintaa. Nyt näet pylväsdiagrammin sadan mittauksen tuloksesta simulaattorin alla. Näet myös mittaustuloksen sekä värillisen pylvään, joka kuvaa mittaustuloksen 1 todennäköisyyttä. Miten voit sanallisesti kuvailla H-portin toimintaa?
Expand by moving mouse over the exercise or by clicking
Käytämme useimmiten kvanttiporttisimulaattorin ulostulon havainnollistamiseen teoreettisesti laskettua todennäköisyysjakaumaa. Tätä voi ajatella todennäköisyysjakaumana, jossa toistoja on tehty valtava määrä. Tällöin H-portti antaa ulostulona eri vaihtoehdot tasan 50% todennäköisyydellä.
Please
Kokeile itse
Tutki usean peräkkäisen H-portin toimintaa ja tee alla oleva tehtävä.
Expand by moving mouse over the exercise or by clicking
Kvanttiportin lopputulos on satunnainen jos mikään ulostulo ei tapahdu täysin varmasti, vaan useamman eri ulostulon todennäköisyys on nollaa suurempi. Yksi H-portti antaa satunnaisen ulostulon. Useampi H-portti peräkkäin voi kuitenkin muuttaa tilanteen ja antaa tietyn ulostulon varmuudella. Tämän näet siitä, että pylväsdiagrammissa on ainoastaan yksi pylväs.
A.5.4 SX-portti
Muistathan vielä X-portin yksinkertaisen toiminnan: bitin arvo 0 vaihtuu arvoon 1 ja vastaavasti 1 muuttuu arvoksi 0. Voiko olla sellaista porttia, joka kahteen kertaan peräkkäin käytettynä tekee saman kuin yksittäinen X-portti? Tavalliselle bitille sellaista ihmeporttia ei ole olemassa, sillä arvojen 0 ja 1 välissä ei ole mitään kolmatta vaihtoehtoa. Sen sijaan kubitille tällainen portti löytyy ja sitä kutsutaan kuvaavasti nimellä -portti tai SX-portti. Jälkimmäisessä 'S' tulee neliöjuuren englanninkielisestä nimityksestä 'square root'.
Please
Kokeile itse
Kokeile SX-portin toimintaa ja vertaa sitä X-portin toimintaan.
Expand by moving mouse over the exercise or by clicking
Kokeilujesi lomassa vastaa seuraavaan kysymykseen.
Tutki vielä usean peräkkäisen SX-portin toimintaa.
Sekä H-portti että SX-portti antavat satunnaisen ulostulon molemmilla syötteillä 0 ja 1. Niitä ei voi erottaa toisistaan pelkästään sen perusteella, miten yksi portti vaikuttaa yksittäiseen kubittiin. Onneksi olet tutustunut myös siihen, miten kaksi perättäistä H-porttia ja kaksi perättäistä SX-porttia toimii. Käytä tätä tietoa seuraavissa tehtävissä. Niissä ei ole näkyvissä todennäköisyysjakaumaa. Onnistut tehtävässä, kun muistat, että kunkin ulostulon kohdalla oleva värillinen alue kuvaa ulostulon 1 todennäköisyyttä.
Please
Tehtävä
Kolmesta kubitista kahteen vaikuttaa tuntematon portti, joka on joko H-portti tai SX-portti. Laita kubittien toisen askeleen kohdalle portti, joka on sama kuin ensimmäisen askeleen kohdalla. Jätä toinen askel tyhjäksi sen kubitin kohdalta, jonka tuntematon portti on tyhjä.
Expand by moving mouse over the exercise or by clicking
Please
Tehtävä
Kuhunkin kubittiin vaikuttaa tuntematon portti, joka voi olla H-portti tai SX-portti. Laita jokaisen kubitin toisen askeleen kohdalle portti, joka on sama kuin ensimmäisen askeleen kohdalla.
Expand by moving mouse over the exercise or by clicking
A.5.5 Kontrolloidut portit
Olemme aikaisemmin käyneet läpi CX-portin ja CCX-portin, joissa joko yksi tai kaksi bittiä kontrolloi sitä, onko X-portti toiminnassa vai ei. Kontrollipalloja voi lisätä mihin hyvänsä yhden kubitin portteihin. Kontrollipallojen määrää ei myöskään ole rajattu.
Please
Kokeile itse
Rakenna erilaisia kontrolloituja H- ja SX-portteja ja testaa niiden toimintaa.
Expand by moving mouse over the exercise or by clicking
Please
Kokeile itse
Rakenna Fredkin-portti ja testaa sen toimintaa. Kolmelle kubitille voit tehdä kolme erilaista Fredkin-porttia. Kokeile niistä jokaista.
Expand by moving mouse over the exercise or by clicking
Onko erilaisia Fredkin-portteja tosiaan kolme?
Fredkin-portti vaikuttaa kolmeen bittiin. Näistä kahteen vaikuttaa swap ja yhdessä on kontrollipallo. Erilaisia Fredkin-portteja on siten kolme ja ne näyttävät tältä: 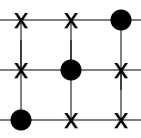
Olemme aikaisemmin jaksossa A.4.6 tehneet kolmen CX-portin avulla piirin, jonka toiminta vastaa yksittäistä swap-porttia. Tämä on hyvä käydä kertaamassa ennen seuraavaa tehtävää, jossa kolmen CCX-portin avulla tehdään Fredkin-portti.
Please
Tehtävä
Tee kolmen CCX-portin avulla sellainen piiri, jonka toiminta vastaa Fredkin-porttia, jossa kontrollipallo on keskellä.
Expand by moving mouse over the exercise or by clicking
CCX-portteja käsittelevässä jaksossa totesimme, että erilaisia CCX-portteja on kolme erilaista:  Jos et muista näiden eroa, niin kannattaa hetkeksi palata CCX-portin esittelevään jaksoon A.4.5. Koska kunkin askeleen kohdalle on vain kolme vaihtoehtoa, voit melko vaivattomasti kokeilla kaikki mahdolliset yhdistelmät läpi. Testausta nopeuttaa se, jos valitset sellaisen syötteen, joka erottaa halutun Fredkin-portin muista Fredkin-porteista. Tämä liittyy tehtävää edeltävään kysymykseen. Lopuksi täytyy toki varmistaa toiminta kaikilla eri syötteillä, sillä yksi syöte ei erota haluttua Fredkin-porttia kaikista muista porteista vaikka rajaakin ainakin vääränlaiset Fredkin-portit pois.
Jos et muista näiden eroa, niin kannattaa hetkeksi palata CCX-portin esittelevään jaksoon A.4.5. Koska kunkin askeleen kohdalle on vain kolme vaihtoehtoa, voit melko vaivattomasti kokeilla kaikki mahdolliset yhdistelmät läpi. Testausta nopeuttaa se, jos valitset sellaisen syötteen, joka erottaa halutun Fredkin-portin muista Fredkin-porteista. Tämä liittyy tehtävää edeltävään kysymykseen. Lopuksi täytyy toki varmistaa toiminta kaikilla eri syötteillä, sillä yksi syöte ei erota haluttua Fredkin-porttia kaikista muista porteista vaikka rajaakin ainakin vääränlaiset Fredkin-portit pois.
A.5.6 Käänteisportti
Olemme aikaisemmin nähneet, että moni portti on sellainen, että sen toiminta kumoutuu kun kaksi samanlaista porttia laittaa peräkkäin. Jos esimerkiksi laitat kaksi X-porttia peräkkäin, vastaa se toiminnaltaan tilannetta, jossa ei ole yhtäkään porttia.
Muistele läpikäymiämme portteja ja vastaa alla olevaan kysymykseen.
Please
Kokeile itse
Kokeile jokaista porttia siten, että laitat saman portin peräkkäin. Vaihtele syötettä.
Expand by moving mouse over the exercise or by clicking
Sellaista porttia, joka kumoaa annetun portin toiminnan, kutsutaan sen käänteisportiksi. Portti voi olla oma käänteisporttinsa, mutta voi myös olla niin, että käänteisportti on jokin muu portti. Joka tapauksessa kvanttiteorian matemaattisesta rakenteesta seuraa, että jokaisella kvanttiportilla on käänteisportti. Tästä voimme päätellä sen, että kvanttiporteista koostuva piiri voidaan kääntää, eli etsiä sellainen yhdistelmä portteja, joka kumoaa piirin toiminnan.
Seuraavassa tehtävässä ruskea laatikko on tuntematon portti. Yhdistele tuntemiamme portteja ja etsi sellainen kombinaatio, joka kumoaa tuntemattoman portin toiminnan. Tämä tarkoittaa, että lopputuloksena syötteen 0 tulee antaa ulostuloksi 0 ja syötteen 1 vastaavasti 1.
Please
Tehtävä
Etsi porttien yhdistelmä, joka kumoaa tuntemattoman portin toiminnan.
Expand by moving mouse over the exercise or by clicking
Tavallisten porttien tapauksessa käänteisportti löytyy kuvailemallamme tavalla, eli etsimällä porttien yhdistelmä, jossa ulostulo on sama kuin syöte kaikilla eri syötteillä. Kvanttiporttien tapauksessa tämä ei kuitenkaan riitä. Mittauksessa kvanttitilasta ei nimittäin paljastu kaikkea, ja portin toiminta saattaa näyttää kumoutuneen vaikka se ei olekaan palauttanut tilaa alkutilaksi. Annetun portin käänteisportti on sellainen portti, joka kumoaa portin vaikutuksen vaikka ne olisivat toisten porttien välissä.
Olemme aikaisemmin jaksossa A.5.3, että kaksi H-porttia peräkkäin ei tee syötteelle mitään. Näin ollen voimme todeta, että kun kubittiin vaikuttaa portti ja käänteisportti kahden H-portin ympäröimänä, tulee ulostulon olla sama kuin syöte.
Please
Kokeile itse
Tässä ?-portti on sama kuin edellä. Laita edellisen tehtävän ratkaisusi ?-portin perään. Onko ulostulo sama kuin syöte?
Expand by moving mouse over the exercise or by clicking
Johtopäätöksenä aikaisemmasta on se, että kvanttiporttien tapauksessa käänteisporttia täytyy testata myös muiden porttien välissä. Aikaisemmin löytämäsi porttien yhdistelmä ei ole tuntemattoman portin käänteisportti, sillä se ei kumoa tuntemattoman portin toimintaa H-porttien välissä. Korostettakoon vielä, että kun tässä puhumme tuntemattomasta portista ja sen käänteisportista, ei kyseessä ole välttämättä mikään aikaisemmin nimeämämme portti. Portti voi olla esimerkiksi yhdistelmäportti kahdesta portista.
Voidaan osoittaa, että yhden kubitin tapauksessa riittää tarkastella portteja ilman muita portteja sekä kahden H-portin ympäröimänä. Yhden kubitin tapauksessa käänteisportti on siis sellainen portti, jossa annetun portin toiminta kumoutuu kaikilla syötteillä
ilman toisia portteja, sekä
H-porttien ympäröimänä.
Alla olevassa kuvassa on havainnollistettu nämä kaksi tilannetta. On olennaista, että vihreä portti, joka kuvaa käänteisporttia, on molemmissa tapauksissa sama. Käänteisportti voi olla usean perusporttimme yhdistelmä ja sen vuoksi se on kuvassa piirretty pidempänä.
Kummassakin näistä tapauksista syötteen tulee mennä läpi muuttumattomana; silloin vihreä portti on tuntemattoman portin käänteisportti.
Palataan aikaisempaan tehtäväämme. Löytämämme tuntemattoman portin käänteisporttiehdokas toteuttaa ehdon (1), mutta ei ehtoa (2). Täytyy siis jatkaa etsintöjä.
Please
Tehtävä
Etsi porttien yhdistelmä, joka kumoaa tuntemattoman portin toiminnan (1) siten, että askeleiden 1 ja 7 kohdalla ei ole mitään sekä (2) siten, että H-portit ovat askeleiden 1 ja 7 kohdalla. Käytä samaa porttien yhdistelmää molemmissa tapauksissa ja laita ne askeleiden 3-6 välille.
Expand by moving mouse over the exercise or by clicking
Tässä olisi ensimmäistä kertaa kaivannut Kvanttipöllön vinkkiä, kun kokeiltavien kombinaatioiden määräkin on jo aika huima.
—Saisiko tähän jotain apua kun ei millään meinaa onnistua?
Kvanttipöllö: Tehtäviin saa vinkkiä keskustelupalstan kautta. En laita niitä tänne marginaaliin, sillä muuten ne näkee nekin jotka eivät vinkkiä halua. Laita sinne kysymys oikean jakson alle ja käytä tehtävän nimeä. Nimen näkee risuaidasta.
—Muistutetaan vielä lopuksi, että mittauksen jälkeen laskentaa ei voi enää peruuttaa takaisin syötteeseen. Kvanttilaskenta on kääntyvää kvanttiporttien osalta, mutta viimeinen vaihe, eli mittaus, ei ole käännettävissä oleva tapahtuma.
A.5.7 Z-portti
Tutustutaan vielä yhteen uuteen kvanttiporttiin. Mieti kysymyksiä ajatuksella, sillä jakson viimeisessä tehtävässä tarvitset niiden kautta oppimiasi tietoja.
Please
Kokeile itse
Z-portti on eräs kvanttiportti. Tutki sen toimintaa.
Expand by moving mouse over the exercise or by clicking
Kuten käänteisportteja käsittelevässä jaksossa totesimme, kvanttiporttien koko toiminta ei tule esille alkutilojen ja
muutoksissa. Tämä johtuu siitä, että kvanttiportti voi jotenkin muuttaa superpositiotiloja muuttamatta lainkaan tiloja
ja
.
Please
Kokeile itse
Tutki Z-portin toimintaa kun se on muiden porttien välissä. Piirissä on XZX, eli Z-portti kahden X-portin välissä. Kokeile X-porttien tilalle muitakin portteja. Toisella kubitilla voit verrata miten portit toimivat ilman Z-porttia.
Expand by moving mouse over the exercise or by clicking
Muistele sitten vielä käänteisportin määritelmä ja käytä edellistä kvanttiporttisimulaattoria etsiäksesi Z-portin käänteisportti. Muista testata yhdistelmän toiminta ilman muita portteja sekä H-porttien ympäröimänä.
Please
Tehtävä
Tee CZ-portin ja H-porttien avulla piiri, jolla on sama toiminta kuin yksitäisellä CX-portilla, jossa X-portti vaikuttaa kubittiin q[0].
Expand by moving mouse over the exercise or by clicking
Ihan aluksi kannattaa muistella CX-portin toiminta. Mene vaikka takaisin simulaattoriin ja tee itsellessi taulukko syötteistä ja ulostuloista. Esim. syöte 00 antaa ulostulon 00 ja syöte 11 ulostulon 01. Entä syötteet 01 ja 10?
Kuten olemme aikaisemmassa kysymyksessä todenneet, niin "Z-portti toimii kahden ------- välissä kuten ----- yksinään." Jos et muista mitkä puuttuvat sanat ovat, niin kertaa aikaisempi osa tästä jaksosta. Tämä on olennainen vihje tehtävän selvittämiseksi.
Z-portti on tyypiltään vaiheportti. Tämä tarkoittaa, että se jättää tilat ja
ennalleen, mutta muuttaa niiden välisiä superpositiotiloja. Vaiheporttien toiminta on sinällään yksinkertaista, mutta niiden kuvaaminen vaatii hieman matematiikkaa. Kubittitilojen ja kvanttiporttien matemaattiseen kuvaukseen pääsemme Kvanttiaakkosten B-osassa. Siellä pystymme täsmällisesti selittämään Z-portin toiminnan.
Porttilaskenta on malli informaation prosessointia suorittavalle laitteelle - siis tietokoneelle. Olemme käyneet porttilaskentaa läpi sen vuoksi, että meillä täytyy olla ensin jokin määritelmä tavalliselle tietokoneelle ennen kuin voimme lähteä miettimään erikoisempien tietokoneiden toimintaa. Tässä kohtaa täytyy mainita, että porttilaskenta on vain yksi malli informaation prosessoinnille ja muitakin malleja on kehitelty.

Kvanttiporttilaskenta on vastaavasti malli kvantti-informaatiota prosessoivalle laitteelle. Tällaista laitetta voi siten luontevasti kutsua kvanttitietokoneeksi. Kvanttitietokone ottaa syötteeksi bittijonon ja antaa ulostuloksi bittijonon, samoin kuten tavallinenkin tietokone. Prosessoinnin aluksi bittijono kirjoitetaan kvanttisysteemin tiloihin. Näin informaatio on kvantti-informaation muodossa ja sitä voidaan muokata kvanttiporteilla. Lopuksi mittaus muuttaa kvantti-informaation takaisin tavalliseksi informaatioksi, siis bittijonoksi. Käymissämme harjoituksissa tämä asetelma on varmasti tullut sinulle selväksi.

Kvanttiporttilaskenta on sinällään melko abstrakti malli kvanttitietokoneelle. Käytännöllisemmästä näkökulmasta katsoen kvanttitietokone on jotakin hieman muuta. Voikin ajatella niin, että porttilaskentaa suorittava laite on tietokoneen prosessori ja kvanttiporttilaskentaa suorittava laite on kvanttiprosessori. Kvanttitietokoneessa tulee olla kummankinlaisia prosessoreita ja vielä muitakin komponentteja. Lisäksi täytyy olla kvanttitietokonetta varten kirjoitettu ohjelma ja sen käyttöön sopiva ohjelmointikieli.

Kvanttifysiikka mahdollistaa kubittien prosessoinnin tavalla, johon bitit eivät väänny. Olemme aikaisemmin tutustuneet H-porttiin, SX-porttiin ja Z-porttiin, joita ei voi suorittaa bitille. Tästä kvanttifysiikan avaamasta laajemmasta ulottuvuudesta tulee odotukset nopeammasta laskennasta. Kun on enemmän mahdollisuuksia perusoperaatioille, voi koittaa keksiä uusia tapoja laskea jokin asia. Kvanttitietokoneen käyttäminen hyödyllisellä tavalla ei kuitenkaan ole mitenkään suoraviivaista. Kvanttitietokone tarvitsee erityisiä kvanttialgoritmeja, jotka sopivalla tavalla hyödyntävät kvanttifysiikan avaamia uusia mahdollisuuksia. Kvanttitietokone ei siis ole taikakalu, joka samantien tekisi kaiken laskennan supertietokoneita nopeammin. Luultavasti kvanttitietokone tulee nopeuttamaan vain tietynlaisten laskentaongelmien ratkaisua.

Kvanttiprosessorin rakentaminen on vaikeaa. Isoin yksittäinen syy on se, että kvanttisysteemit ovat alttiita melulle ja häiriolle. Kun melua on liikaa, ei kvanttisysteemi ole sen kummempi kuin klassista fysiikkaa noudattava systeemi. Melu siis tuohoaa systeemin kvanttiominaisuudet. Kvanttifysiikassa sitä aikaa, jonka kvanttisysteemi säilyttää kvanttiominaisuutensa, kutsutaan koherenssiajaksi. Sitä ilmiötä tai tapahtumaa, jossa kvanttiominaisuudet menetetään, kutsutaan dekoherenssiksi. 
Kun mennään tarkemmin kvanttiprosessorin edellytyksiin, on hyvänä lähtökohtana DiVincenzon kriteerit kvanttiprosessorille. Ne ovat ikään kuin muistilista kvanttiprosessorin rakentajalle niistä seikoista, jotka täytyy saada kuntoon. DiVincenzon kriteerit ovat seuraavat:
- Skaalautuva määrä kubitteja. Skaalautuvuus tarkoittaa, että kubitteja voidaan lisätä tarpeen mukaan. Tyypillisesti laskentaongelman vaikeuden noustessa tarvittavien kubittien määrä kasvaa. Kubitteja tarvitaan lisäksi virheenkorjaukseen. Tämä kurssin harjoituksissa olemme tehneet hyvin yksinkertaisia toimenpiteitä ja kubittien lukumäärä on siitä syystä ollut pieni.
- Mahdollisuus alustaa laskennassa käytetyt kubitit, eli preparoida ne toistuvasti alkutilaan. Laskennan kannalta on tärkeää, että kubitit ovat alussa tunnetussa alkutilassa. Samaan tilaan pitää voida palata aina, kun laskenta halutaan toistaa. Kvanttiporttilaskennassa alkutila on yleensä se tila, jossa jokainen kubitti on tilassa
.
- Riittävän pitkä koherenssiaika. Koherenssiajalle ei voi antaa tiettyä kynnysarvoa, vaan sen riittävyys on suhteessa prosessoinnin nopeuteen. Kubiteille pitää ehtiä tekemään halutut prosessoinnit koherenssiajan aikana. Kvanttiporttilaskennassa prosessointi vastaa porttien toteuttamista.
- Universaali kvanttiporttijoukko. Kvanttiporttijoukkoa sanotaan universaaliksi, jos sillä voidaan suorittaa mikä hyvänsä kvanttiportti, tai vähintäänkin approksimoida niin tarkasti kuin halutaan. Tämä tarkoittaa, että universaali kvanttiporttijoukko mahdollistaa minkä hyvänsä kvanttialgoritmin toteuttamisen. Voidaan osoittaa, että yhden ja kahden kubitin kvanttiportteja yhdistelemällä voidaan toteuttaa kaikki useamman kubitin kvanttiportit.
- Kubittien mittaaminen. Mittaus on oleellinen osa kvanttilaskentaa, sillä laskennan lopullinen tulos on mittauksessa saatava bittijono. Kvanttisysteemien kantamaa informaatiota ei voi lukea ilman mittausta. Mittausprosessin tulee olla luotettava ja toistettavissa oleva.

Riippuen kvanttiprosessorin fysikaalisesta toteutuksesta ovat jotkin portit natiiveja, eli sellaisia, jotka voidaan suorittaa suoraan. Muut portit rakentuvat natiiviporttien yhdistelminä. Rajallisen koherenssiajan takia on suotavaa pyrkiä tekemään haluttu informaation prosessointi käyttäen niin pientä määrää portteja kuin mahdollista. Tosin myös natiiviporttien suoritusajassa voi olla eroa, joten asia on tätäkin monimutkaisempi. Joka tapauksessa piirin muuttaminen erilaiseksi, mutta saman prosessoinnin suorittavaksi piiriksi, on kvanttialgoritmin ajamisen suunnittelussa tärkeää. Aikaisemmissa harjoituksissa olet päässyt etsimään tietyille piireille vaihtoehtoisia toteutuksia. Esimerkiksi jaksossa A.4.6 näimme, että swap-portin voi rakentaa CX-porttien avulla.
A.6 Harjoitustehtäviä
Tämä jakso aukeaa kurssille kirjautuneille opiskelijoille, kun aikaisemmat tehtävät on suoritettu.
Tämä jakso aukeaa sitten, kun olet tehnyt kaikki aikaisemmat tehtävät. Pääset vielä kertaamaan ja harjoittelemaan oppimiasi asioita kvanttiporttisimulaattorin avulla. Tehtävät saattavat vaatia useita kokeilukertoja.
A.7 Loppusanat
Tämä jakso aukeaa kurssille kirjautuneille opiskelijoille, kun kaikki tehtävät on suoritettu.
Tämä jakso aukeaa sitten, kun olet vastannut kaikkiin kysymyksiin ja tehnyt kaikki tehtävät. Voit tarkistaa Suoritukset -kohdasta vielä tekemättä olevat kysymykset ja tehtävät.
Lista kvanttiporteista
Sinisellä ovat sellaiset kvanttiportit, jotka toimivat myös biteille. Violetilla ovat sellaiset kvanttiportit, jotka toimivat ainoastaan kubiteille.
Kahden kubitin portit
- CX-portti = kontrolloitu X-portti = CNOT-portti
- swap-portti = vaihto-portti
- CZ-portti = kontrolloitu Z-portti
Kolmen kubitin portit
- CCX-portti = Toffoli-portti
- Fredkin-portti = kontrolloitu swap-portti
Please
Kokeile itse
Täällä voit kokeilla kvanttiporttien toimintaa.
Expand by moving mouse over the exercise or by clicking
Please
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.

Muistiinpanon kirjoittamista marginaaliin kutsutaan TIMissä kommentoinniksi. Kommentointi kannattaa ottaa aktiiviseksi osaksi opiskelua. Kommentointi onnistuu seuraavalla tavalla:
Huom! Vaikka kirjoittaisit kommentin kaikille, ei siinä näy nimeäsi. Voit hyvin jakaa ajatuksesi myös muille.
Jos olet siirtänyt muokkausvalikon lohkon vasemmalle puolelle, klikkaa lohkoa, jolloin sen oikealle puolelle tulee C-kirjain (Comment), klikkaa C-kirjainta