DY:n ratkaiseminen osa 1

Ratkaisemisesta yleisesti

Kynällä ja paperilla ratkottavat differentiaaliyhtälöt ovat helppoja erikoistapauksia. Niissäkin usein valistunut arvailu on tehokasta.

Tällä sivulla on esiteltynä keskeisimpiä tavallisten DY:iden ratkaisumenetelmiä, käsitteistä voit lukea tarkemmin DY-etusivulla.

Separointi: separoituvat 1.kl DY:t
Vakion variointi: 1.kl lineaariset DY:t
VLHDY:nVakiokertoiminen, Lineaarinen, Homogeeninen DY ratkaisukaava
Määräämättömien kertoimien menetelmä: VLEDYVakiokertoiminen, Lineaarinen, Epähomogeeninen DY:t.

Esimerkeissä on lisäksi mukana alkuarvotehtäviä.

Seuraavia aiheita käsitellään DY:n ratkaiseminen 2 -sivulla:

DY-ryhmät
Numeeriset ratkaisumenetelmät
Reuna-arvotehtävät
Ominaisarvotehtävät
Sarjaratkaisut ja erikoispolynomit.

Separoituva DY

Ensimmäisen kertaluvun DY on separoituva, jos se voidaan esittää muodossa $\red y'(\green x)=g(\green x)h(\red y),$ missä $\red y$ on ratkaistava funktio, jonka muuttujana on $\green x$ .

Separoituvan DY:n ratkaisukaava on $\int \frac{\text d\red y}{h(\red y)}=\int g(\green x)\,\text d\green x,$ josta voidaan integroinnin jälkeen ratkaista funktio $\red y(\green x)$ .

Muistisääntö

Derivaatta voidaan kirjoittaa $\red y'(\green x) = \dfrac{\text d\red y}{\text d\green x},$ jolloin separoituva yhtälö on

$\frac{\text d\red y}{\text d\green x}=g(\green x)h(\red y).$

Tästä voidaan erotella eli separoida $\red y$ - ja $\green x$ -termit integrointia varten

$\int \frac{\text d\red y}{h(\red y)}=\int {g(\green x)\,\text d\green x}.$

Alkuarvotehtävään $\red y(\green x_0)=\red y_0$ saadaan ratkaisu suoraan integraalista

$\int_{\red y_0}^{\blue y} \frac{\text d\red y}{h(\red y)} =\int_{\green x_0}^{\blue x} g(\green x)\,\text d \green x,$ missä ylärajoja $\blue y$ ja $\blue x$ käsitellään kuin vakioita. Integroinnin ja sijoituksen jälkeen voidaan ratkaista $\blue y(\blue x).$

Esimerkiksi $\red y'(\green x)=-\green x\red y^2$ on separoituva DY, josta voidaan lukea funktiot $g(\green x)= -\green x$ ja $h(\red y)=\red y^2.$

Homogeeninen yhtälö $\red y'+g(\green x)\red y=0$ on aina separoituva, jossa $h(\red y) = -\red y.$

Esimerkkejä

Esimerkki 1: $\red y'(\green x) = -\green x\red y(\green x)^2$

Funktiot ovat $g(\green x)= \green x$ ja $h(\red y)=-\red y^2$ , joten $\int -\frac{\text d\red y}{\red y^2}=\int \green x \,\text d\green x, \quad \red y \neq 0.$ Integroimissäännöillä saadaan $\frac{1}{\red y}=\frac{1}{2}\green x^2 + \blue C = \frac{\green x^2 + \violet C'}{2},$ missä $\blue C = 2\violet C'$ on määräämätön integroimisvakio. Vakio voi muuttua, kun yhtälöä muokataan, mutta sitä voidaan merkitä samalla symbolilla. Puolittain integroitaessa molemmille puolille saadaan oma vakio, mutta nämä voidaan siirtää samalle puolelle yhdeksi vakioksi.

Nyt voidaan ratkaista $\red y$ $\red y= \frac{2}{\green x^2 + \violet C'}.$ Tarkistus derivoimalla: $\red y'(\green x) = D\Big(\frac{2}{\green x^2 + \violet C'}\Big)=-\frac{4\green x}{(\green x^2 + \violet C')^2}=-\green x\red y^2.$

Nollalla jakaminen

Jos funktiolla $h(\red y(\green x))$ on nollakohtia, ne täytyy tarkastella erikseen. Jos derivaatta on $\red y'(\green x)=g(\green x)h(\red y(\green x))=0,$ täytyy ratkaisujen $\red y(\green x)$ olla vakioita $D(\text{vakio})=0$ .

Esimerkissä 1 funktio $h(\red y(\green x))=\red y(\green x)^2,$ joten DY:n toteuttaa myös funktio $\red y(\green x)=0$ kaikilla $\green x$ .

Miten integroin funktion $\red y(\green x)$ suhteen?

Separoituvien DY:iden yhteydessä puhutaan joskus funktiosta $\red y=\red y(\green x)$ muuttujana. Sanotaan, että separoidaan muuttujat $\green x$ ja $\red y$ eli erotellaan ne yhtälön eri puolille.

Separoinnissa funktion $\red y$ riippuvuus muuttujasta $\green x$ voidaan hetkeksi unohtaa, ja sitä voidaan käsitellä kuin tavallista muuttujaa.

Esimerkki 2: $\red y'(\green x) = \frac{\red y(\green x)^2}{\green x}$

Separoituva DY voidaan ratkaista kirjoittamalla $\red y'(\green x)= \frac{\text d\red y}{\text d\green x}$ , tässä tapauksessa

$\frac{\text d\red y}{\text d\green x}=\frac{\red y^2}{\green x}, \hspace{1cm} \green x\neq 0,$ josta erotellaan eli separoidaan $\green x$ ja $\red y$ yhtälön eri puolille:

$\frac{\text d\red y}{\red y^2}=\frac{1}{\green x}\,\text d\green x, \hspace{1cm} \red y^2\neq 0.$ Nyt voidaan integroida puolittain $\int \frac{\text d\red y}{\red y^2}= \int \frac{1}{\green x}\,\text d\green x,$ jolloin integroimissäännöillä saadaan $-\frac{1}{\red y}=\ln(\green x) + C, \hspace{1cm} \green x > 0.$ Ratkaisu on siis $\red y=\frac{1}{C-\ln(\green x)}, \hspace{1cm} \green x\neq e^C.$ Mikäli tiedossa on jokin reunaehto, esimerkiksi alkuarvo $\red y(\green 1)=1$ , voidaan integroimisvakio määrittää sijoittamalla: $\red y(\green 1)=\frac{1}{C-\ln(\green 1)}=\frac{1}{C}=1,$ eli C = 1 .

Tarkistus derivoimalla: $\red y'(\green x) = D\Big(\frac{1}{C-\ln(\green x)}\Big)=\frac{1}{\green x(C-\ln(\green x))^2}=\frac{\red y^2(\green x)}{\green x}.$ Muista derivaatan laskusäännöt:
ketjusääntö $D\big(f(g(\green x))\big) = f'(g(\green x))g'(\green x)$ ja logaritmi $D\big(\ln(\green x))\big) = 1/\green x$ !

Sovelluksia

Sovellus 1: Kappaleen putoamisliike

Vapaassa pudotuksessa -massaiseen kappaleeseen vaikuttaa liikettä kiihdyttävä painovoima m g, missä on vakiokiihtyvyys, sekä jarruttava vastusvoima $-m k\red v,$ missä k>0 on vakio ja $\red v = \red v(\green t)$ on ajan $\green t$ mukaan muuttuva nopeus, joka halutaan ratkaista.

Newtonin toinen laki, F = ma, on tällöin $F_{\text{tot}}= \cancel m g - \cancel m k \red v = \cancel ma.$ Koska $a=\dfrac{\text d \red v}{\text d\green t},$ saadaan $\frac{\text d\red v}{\text d\green t} = g- k \red v.$ Tämä on separoituva DY $v'(\green t)= f(\green t)h(\red v),$ kun $f(\green t) = 1$ ja $h(\red v) = g- k \red v$ .. Funktion $\red v$ ratkaisemiseksi separoidaan $\red v$ ja $\green t$ $\text d\green t = \frac{\text d\red v}{ g- k \red v}.$

Yksinkertaisilla alkuarvoilla säästytään myöhemmin integroimisvakion selvittämiseltä. Oletetaan, että kappale lähtee hetkellä $\green t= \green 0$ levosta eli $\red v(\green 0) = \red 0.$ Millä tahansa myöhemmällä ajanhetkellä $\blue t$ on nopeus $\red v(\blue t)$ , jota merkitään yksinkertaisesti $\blue v.$

Ylärajat $\blue t$ ja $\blue v$ näyttävät muuttujilta, mutta ne ovat integraalissa vakioita, joista tarvitsee välittää vasta sijoituksessa.

Nyt voidaan integroida puolittain näillä rajoilla. $\int_{\green 0}^{\blue t} \text d\green t = \int_{\red 0}^{\blue v} \frac{\text d\red v}{ g- k \red v},$ josta integroimissäännöillä saadaan $\blue t = -\frac{1}{ k}\,\intsub {\red 0} {\blue v} \ln( g- k \red v).$ Kerrotaan puolittain vakiolla ja sievennetään sijoitus $\ln( g- k \blue v)-\ln( g)=\ln(\frac{ g- k \blue v}{ g})$ logaritmin laskusäännöillä $-k\blue t = \ln(1-\frac{ k}{ g}\blue v).$ Tästä on helppoa ratkaista $\blue v(\blue t) = \red v(\green t).$ Hävitetään logaritmi eksponenttifunktiolla $\exp(x) =e^x$ $\exp(- k\green t) = \cancel\exp\big(\cancel\ln(1-\frac{ k}{ g}\red v)\big)=1-\frac{ k}{ g}\red v.$ Tarvitsee enää järjestellä uudelleen, ja saadaan $\red v(\green t) = \frac{ g}{ k}(1-e^{- k\green t}).$ Fysikaalinen huomio: nopeus lähestyy terminaalinopeutta $\displaystyle{v_t=\lim_{t\to\infty}\red v=\frac{ g}{ k}}$ . Esimerkiksi arvolla k = 0.1 on $v_t=98.1 \text m/\text s.$

Sovellus 2: Veneen moottori sammunut

Sammutetaan liikkuvan veneen moottori. Veneen nopeudelle $\red v=\red v(\green t)$ saadaan Newtonin toisesta laista differentiaaliyhtälö $\red v'(\green t)=\frac{\text d \red v}{\text d\green t} = -\alpha e^{\beta \red v}$ tietyin oletuksin vastusvoimista, joita kuvaavat positiiviset vakiot $\alpha$ ja $\beta$ .

Tämä on separoituva DY, jossa tuntematon funktio on $\red v=\red v(\green t)$ ja separoitavina ovat $g(\green t) = -\alpha$ ja $h(\red v)=e^{\beta \red v}$ Nyt $\dfrac{1}{h(\red v)} = e^{-\beta \red v}$ .

Merkitään moottorin sammumishetkellä $\green t=\green 0$ nopeutta $\red v(\green 0)=\red v_0$ . Jollain myöhemmällä ajanhetkellä $\blue t$ on veneen nopeus $\red v(\blue t)=\blue v$ . Näillä tiedoilla saadaan määrätyt integraalit $\dint_{\red v_0}^{\blue v} e^{-\beta \red v}\,\text d \red v = \dint_{\green 0}^{\blue t} -\alpha\, {\text d\green t}$ ja integroinnin tuloksena $\intsub {\red v_0} {\blue v} -\frac{1}{\beta}e^{-\beta \red v}= -\frac{1}{\beta}e^{-\beta \blue v}+ \frac{1}{\beta}e^{-\beta \red v_0} = -\alpha \blue t.$ Tästä voidaan ratkaista $\blue v(\blue t) = \red v(\green t).$ Siirretään alkunopeuden $\red v_0$ sisältävä termi ja kerrotaan vakiolla $-\beta$ puolittain $e^{-\beta \red v}=\alpha\beta \green t+e^{-\beta \red v_0}.$ Tuodaan nopeus alas eksponentista logaritmilla $\cancel\ln\big(\cancel e^{-\beta \red v}\big) = -\beta \red v = \ln\big(\alpha\beta \green t+e^{-\beta \red v_0}\big).$ Näin saadaan nopeus $\red v(\green t) = -\frac{1}{\beta}\ln\big(\alpha\beta \green t+e^{-\beta \red v_0}\big).$ Huomaa, että nopeus on positiivinen, kunhan $0 < \alpha\beta \green t+e^{-\beta \red v_0} < 1$ .

Tästä voidaan vielä jatkaa. Jos haluamme tietää veneen paikan $\red x=\red x(\green t)$ jollain ajanhetkellä, kirjoitetaan nopeus paikan muutoksena ja saadaan uusi DY. Veneen pysähtymismatka voidaan tällöin määrittää alkunopeuden perusteella.

Sovellus 3: Veneen pysähtymismatka

Edellisestä tuloksesta saadaan veneen sijainnille $\red x=\red x(\green t)$ uusi separoituva DY $\red v(\green t) = \red x'(\green t) = \frac{\text d\red x}{\text d\green t}= -\frac{1}{\beta}\ln\big(\alpha\beta \green t+e^{-\beta \red v_0}\big).$ Olkoot moottorin sammumishetkellä $\green t=\green 0$ veneen sijainti $\red x(\green 0)=\red 0$ ja veneen pysähtymishetkellä $\green t= \green t_1$ sijainti $\red x(\green t_1)=\red x_1.$ Pysähtymishetki voidaan ratkaista yhtälöstä $\red v(\green t_1) = -\frac{1}{\beta}\ln\big(\alpha\beta \green t_1+e^{-\beta \red v_0}\big) = 0.$ Logaritmi on nolla, kun sen sisältö on 1, eli $\green t_1 = \frac{1}{\alpha\beta}(1-e^{-\beta \red v_0}).$ Nyt tiedetään integrointirajat. Separoidaan yhtälö ja integroidaan $\int_{\red 0}^{\red x_1}\, \text d\red x=\int_{\green 0}^{\green t_1}-\frac{1}{\beta}\ln\big(\alpha\beta \green t+e^{-\beta \red v_0}\big)\,\text d\green t.$

Tämä näyttää hieman pelottavalta, joten lakaistaan maton alle logaritmin sisältö, ja merkitään $\violet u(\green t)=\alpha\beta \green t+e^{-\beta \red v_0}.$

Sijoitusta varten lasketaan $\violet u(\green 0)=\violet e^{-\beta \red v_0}$ ja $\violet u(\green t_1)=\violet 1.$

Nyt $\dfrac{\text d\violet u}{\text d\green t} = \alpha\beta$ , joten $\text d\green t = \dfrac{\text d\violet u}{\alpha\beta}$ ja integraali on $\int_{\red 0}^{\red x_1}\, \text d\red x =-\frac{1}{\alpha\beta^2}\int_{\violet e^{-\beta \red v_0}}^{\violet 1} \ln(\violet u)\,\text d\violet u.$ Tästä saadaan logaritmin integraalilla $\dint \ln(\red x)\,\d\red x = \red x(\ln(\red x)-1)$ $\red x_1 =\frac{1}{\alpha\beta^2} \intsub {\violet e^{-\beta \red v_0}}{\violet 1} \violet u(1-\ln(\violet u)).$ Sijoituksesta saadaan lopputulos $\red x_1 = \frac{1}{\alpha\beta^2} (1-e^{-\beta \red v_0}(1+\beta \red v_0)).$

Ratkaisukaavan todistus ja tulosten yksikäsitteisyys

Olkoot ja jatkuvia funktioita ja sellainen, että $h(y(x))\not=0$ kaikille . Tällöin y(x) on yhtälön y'(x)=g(x)h(y) ratkaisu jos, ja vain jos y(x) toteuttaa yhtälön $\int \frac{1}{h(y)}\,\dy=\int g(x)\,\dx+C,~C\in\mathbb{R}.$

Todistus: Olkoon y(x) yhtälön y'=g(x)h(y) ratkaisu. Tällöin $\frac{y'(x)}{h(y(x))}=g(x)$ kaikille Analyysin peruslauseen nojalla tämä on yhtäpitävää sen kanssa, että on olemassa vakio $C\in\mathbb{R}$ , jolle $\int \frac{y'(x)}{h(y(x))}\,\dx=\int g(x)\, \dx +C.$ Muuttujanvaihdolla t=y(x) saadaan $\int \frac{1}{h(t)}\,\dt=\int g(x) \,\dx +C.$

Ratkaisun olemassaolo ja yksikäsitteisyys

Alkuarvotehtävällä $\begin{equation*} \begin{cases} y'(x)=g(x)h(y)=f(x,y)\\ y(x_0)=y_0 \end{cases} \end{equation*}$ on ratkaisu pisteen (x_0,y_0) ympäristössä, jossa f(x,y) on jatkuva. Ratkaisu on yksikäsitteinen, jos $f_y=\frac{\partial f}{\partial y}$ on jatkuva. Tämä tulos tunnetaan Picardin-Lindelöfin lauseena.

Vakion variointi

Vakion varioinnilla tarkoitetaan vakion muuttamista tuntemattomaksi funktioksi. Tätä voidaan hyödyntää esimerkiksi lineaarisen ensimmäisen kertaluvun DY:n ratkaisemisessa.

Lineaarinen 1.kl DY

$\red y'(\green x)+a(\green x)\red y(\green x)=b(\green x)$ Tämän ratkaiseminen onnistuu seuraavalla tavalla:

ratkaistaan separoimalla homogeeninen DY $\red y'(\green x)+a(\green x)\red y(\green x)=0$
käytetään homogeenisen osan ratkaisuun vakion variointia ja sijoitetaan yrite alkuperäiseen DY:hyn
ratkaistaan näin saatu yksinkertainen DY $\red y'(\green x)=f(\green x)$ integroimalla.

Esimerkkejä

Esimerkki 1 $\red y'(\green x)-\frac{\red y(\green x)}{\green x}=3\green x^3$

DY:n homogeenisen osan ratkaisu saadaan separoimalla: $\begin{align*} \red y'(\green x)-\frac{\red y(\green x)}{\green x}&=0\\ \frac{\text d\red y}{\text d\green x}&=\frac{\red y({\green x})}{\green x}\\ \int\frac1{\red y}{\text d\red y}&=\int\frac1{\green x}\text d\green x\\ \log(|\red y|)&=\log(|{\green x}|)+C\\ \red y({\green x})&=\blue C\green x. \end{align*}$ Käytetään vakion variointia integrointivakioon $\blue C,$ eli asetetaan $\blue C=\blue f(\green x).$ Näin saadaan $\red y(\green x)=\blue f(\green x)\green x,$ jolloin derivaatta on $\red y'(\green x)=\green x\blue f'(\green x)+\blue f(\green x).$ Sijoittamalla nämä ratkaistavana olevaan DY:hyn saadaan $\begin{align*} \red y'(\green x)-\frac{\red y(\green x)}{\green x}&={\green x}\blue f'({\green x})+\blue f({\green x})-\frac{\blue f({\green x}){\green x}}{\green x}\\ &={\green x}\blue f'({\green x})\\ &=3{\green x}^3. \end{align*}$ Siispä funktiolle $\blue f$ pätee $\begin{align*} {\green x}\blue f'({\green x})=3{\green x}^3\\ \blue f'({\green x})=3{\green x}^2\\ \blue f({\green x})={\green x}^3+C_2. \end{align*}$ DY:n ratkaisu on siis $\red y({\green x})=\blue f({\green x}){\green x}=({\green x}^3+C_2){\green x}=\green x^4+C_2\green x.$

Esimerkki 2 Vakiokertoimisen DY:n ratkaisu $\red y'(\green x)=-a\red y(\green x)+b$

Homogeenista osaa vastaa DY $\red y'(\green x)=-a\red y(\green x),$ jonka ratkaisu on $\red y(\green x)=\blue Ce^{-a\green x}.$ Käytetään vakion variointia, eli asetetaan $\blue C=\blue f(\green x).$ Tällöin $\red y(\green x)=\blue Ce^{-a\green x}=\blue f(\green x)e^{-a\green x},$ jonka derivaatta on $\red y'(\green x)=\blue f'(\green x)e^{-a\green x}-a\blue f(\green x)e^{-a\green x}.$ Sijoittamalla nämä alkuperäiseen DY:hyn saadaan $\begin{align*} b=\red y'(\green x)+a\red y(\green x)&=\blue f'(\green x)e^{-a\green x}-a\blue f(\green x)e^{-a\green x}+a\blue f(\green x)e^{-a\green x}\\ &=\blue f'(\green x)e^{-a\green x}, \end{align*}$ joten $\begin{align*} \blue f'(\green x)e^{-a\green x}&=b\\ \blue f'(\green x)&=be^{a\green x}\\ \blue f(\green x)&=\frac bae^{a\green x}+C_2. \end{align*}$ DY:n ratkaisu on siis $\red y(\green x)=\blue f(\green x)e^{-a\green x}=\frac ba+C_2e^{-a\green x}.$

Esimerkki 3 Yleinen ratkaisukaava $\red y'(\green x)=a(\green x)\red y(\green x)+b(\green x)$

Ratkaistaan homogeeniosa separoimalla: $\begin{align*} \red y'(\green x)&=a(\green x)\red y(\green x)\\ \frac{\text d\red y}{\text d\green x}&=a(\green x)\red y(\green x)\\ \int\frac1{\red y}\text d\red y&=\int a(\green x)\text d\green x\\ \log(|\red y|)&=A(\green x)+C\\ \red y(\green x)&=\blue Ce^{A(\green x)}. \end{align*}$ Funkio $A(\green x)=\int a(\green x)\text d\green x$ on jokin $a(\green x)\text{:n}$ integraalifunktio. Jatketaan vakion varioinnilla $\blue C=\blue f(\green x),$ jolloin saadaan $\red y(\green x)=\blue f(\green x)e^{A(\green x)},$ jonka derivaatta on $\red y'(\green x)=\blue f'(\green x)e^{A(\green x)}+a(\green x)\blue f(\green x)e^{A(\green x)}.$ Sijoittamalla nämä ratkaistavaan DY:hyn saadaan $\begin{align*} \red y'(\green x)-a(\green x)\red y(\green x)&=\blue f'(\green x)e^{A(\green x)}=b(\green x)\\ \blue f'(\green x)&=b(\green x)e^{-A(\green x)}\\ \blue f(\green x)&=\int b(\green x)e^{-A(\green x)}\text dx+C.\\ \end{align*}$

Näin ollen ensimmäisen asteen lineaarisen DY:n yleinen ratkaisu on $\red y(\green x)=\blue f(\green x)e^{A(\green x)}=Ce^{A(\green x)}+e^{A(\green x)}\int b(\green x)e^{-A(\green x)}\text dx.$ Tämä ratkaisukaava voi johtaa hankaliin integraaleihin eikä siksi välttämättä ole se helpoin ratkaisutapa.

Vakiokertoiminen lineaarinen homogeeninen DY

Yleisesti toisen kertaluvun VLHDY on muotoa $A\red y''(\green x)+B\red y'(\green x)+C\red y(\green x)=0,$ kun ratkaistava funktio on $\red y(\green x)$ ja A,B ja ovat vakioita.

Mikä ihmeen VLHDY?

Yllä esitelty differentiaaliyhtälö on

vakiokertoiminen (V), koska
- korkeimman derivaatan $\red y''(\green x)$ kerroin on vakio
- alempien derivaattojen $\red y'(\green x)$ ja $\red y(\green x)$ "Nollas" derivaatta! kertoimet ja ovat vakioita
lineaarinen (L), koska
- jokaisessa termissä on tekijänä
  - funktio $\red y(\green x)$
  - tai sen jokin derivaatta.
homogeeninen (H), koska
- siinä ei ole funktiosta $\red y(\green x)$ riippumatonta termiä.

VLHDY:n karakteristinen yhtälö (KY) on $A\blue r^2+B\blue r+C=0,$ missä vakiot ja ovat samat kuin yllä ja $\blue r$ on karakteristisen yhtälön muuttuja.

Mikä ihmeen karakteristinen yhtälö?

Karakteristinen yhtälö saadaan VLHDY:stä sijoituksella $\red y(\green x) = e^{\blue r\green x},$ missä $\blue r$ on vakio. Tämän derivaatat ovat $\red y'(\green x) = \blue re^{\blue r\green x}\text{ eli }\blue r\red y(\green x)$ ja $\red y''(\green x) = \blue r^2e^{\blue r \green x}\text{ eli }\blue r^2\red y(\green x).$

Sijoittamalla nämä VLHDY:hyn $A\red y''(\green x)+B\red y(\green x)+C\red y(\green x)=0$ saadaan se kirjoitettua muotoon $\red y(\green x)(A\blue r^2+B\blue r+C)=0.$ Nyt jakamalla puolittain funktiolla $\red y (\green x)$ saadaan karakteristinen yhtälö $A\blue r^2+B\blue r+C=0.$

DY:n ratkaisut saadaan tämän karakteristisen yhtälön ratkaisujen eli juurten avulla seuraavista kaavoista:

Näissä kaavoissa K_1 ja K_2 ovat vakioita, jotka voidaan selvittää alkuarvojen avulla.

Ratkaisujen sini- ja kosinifunktiot tulevat kompleksisista KY:n juurista Eulerin kaavalla $e^{ix}=\cos(x)+i\sin(x)$ .

Miten lasketaan yhtälön kompleksiset juuret?

Toisen asteen yhtälön ratkaisukaavasta saadaan myös kompleksiset ja imaginääriset juuret.

Lyhyesti: Toisen asteen yhtälön $a\blue r^2+b\blue r+c=0$

juuret ovat kompleksiset, jos diskriminantti ,
juurissa on vain imaginääriosa, jos edellisen lisäksi ,

kun ja ovat reaalisia vakioita ja $\blue r$ yhtälön muuttuja.

Pitkästi: Tutkitaan esimerkiksi toisen asteen yhtälöä r^2-2r+4=0, jolla ei ole reaalisia juuria. Sijoitetaan kertoimet toisen asteen yhtälön ratkaisukaavaan: $\begin{align*} r&=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ &=\frac{2\pm\sqrt{(-2)^2-4\cdot1\cdot5}}{2\cdot1}\\ &=\frac{2\pm\sqrt{-16}}{2}\\ &=\frac{2\pm4\green{\sqrt{-1}}}{2}\\ &=1\pm2\green{\sqrt{-1}}. \end{align*}$ Muistetaan, että $\green{\sqrt{-1}} = \green i,$ joten tulos voidaan kirjoittaa muodossa $r = \blue1\pm \red2 \green i.$ Jos kyseessä on DY:n karakteristinen yhtälö, on DY:n ratkaisu $y(x) = e^{\blue1x}[K_1\cos(\red2x) + K_2\sin(\red2x)].$ Vakiot K_1 ja K_2 voidaan määrätä alkuehdoilla.

Esimerkkejä

Esimerkki 1: $\red y''(\green x)-2\red y'(\green x)+\red y(\green x)=0$

Ensiksi muodostetaan DY:n karakteristinen yhtälö. Vakiot ovat A=1, B=-2 ja C=1, joten karakteristinen yhtälö on r^2-2r+1=0. Tämän juuret löydetään esimerkiksi toisen asteen yhtälön ratkaisukaavalla. Toinen vaihtoehto on tekijöihin jako r^2-2r+1 =(r-1)^2 = 0, josta voidaan lukea, että yhtälöllä on yksi juuri $\red {r_0}=1$ . Tämän perusteella DY:n ratkaisu on $\red y({\green x}) = (K_1+K_2{\green x})e^{\red {\green x}}.$ Tarkistetaan vielä derivoimalla: $\begin{cases} \red y({\green x}) = (K_1+K_2{\green x})e^{\green x}\\ \red y'({\green x}) = (K_1+K_2{\green x})e^{\green x} + K_2e^{\green x}\\ \red y''({\green x}) = (K_1+K_2{\green x})e^{\green x} + 2K_2e^{\green x}. \end{cases}$ Tästä nähdään, että $\red y({\green x})-2\red y'({\green x})+\red y''({\green x})=0,$ kuten pitääkin.

Esimerkki 2: Alkuarvotehtävä

Ratkaistaan alkuarvotehtävä $\begin{cases} \red y(\green 0)=3\\ \red y'(\green \pi)=0\\ \red y''(\green x)-2\red y'(\green x)+5\red y(\green x)=0. \end{cases}$ Lasketaan DY:n karakteristisen yhtälön juuret toisen asteen yhtälön ratkaisukaavalla $\begin{align*} r^2-2r+5&=0\\ r&=\frac{2\pm\sqrt{4-4\cdot5}}{2}\\ r &= \blue1\pm\red2i. \end{align*}$ Juuret ovat kompleksilukuja, joten DY:n ratkaisu on $y(x)=e^{\blue x}[K_1\cos(\red2x)+K_2\sin(\red2x)].$ Alkuarvotehtävää varten tarvitsemme myös ratkaisun derivaatan $y'(x)=e^x[K_1(\cos(\red2x)-\red2\sin(\red2x))+K_2(\sin(\red2x)+\red2\cos(\red2x))].$ Sijoittamalla alkuarvot saadaan yhtälöpari $\begin{cases} \red y(\green 0)=K_1=3\\ \red y'(\green \pi)=e^{\green\pi}(K_1+2K_2)=0, \end{cases}$ jonka ratkaisuilla $K_1=\blue 3$ ja $K_2=\blue {-\frac{3}{2}}$ saadaan alkuarvotehtävän ratkaisu $\red y(\green x)=e^{\green x}[\blue 3\cos(2\green x)\blue{-\frac{3}{2}}\sin(2\green x)].$

Sovelluksia

Sovellus 1: Harmoninen värähtelijä

Tarkastellaan yksiulotteista harmonista värähtelijää.

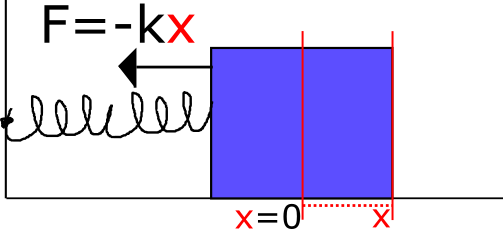
Kappaleen siirtäminen pois tasapainoasemasta saa aikaan jousivakiosta riippuvan voiman $F=-k\red x$ .

Merkitsemällä kappaleen sijaintia funktiolla $\red x(\green t)$ ja tiedolla $F=ma=m\red x''(\green t)$ saamme DY:n $m\red x''(\green t)=-k\red x(\green t).$ Muodostetaan ja ratkaistaan tämän karakteristinen yhtälö $\begin{align*} m\blue r^2+k&=0\\ \blue r^2&=-\frac{k}{m}\\ \blue r&=\pm i\blue{\sqrt{\frac{k}{m}}}. \end{align*}$ Saaduissa juurissa esiintyvä $\blue{\sqrt{\frac{k}{m}}}$ on värähtelyn kulmataajuus, joten merkitään tätä symbolilla $\blue\omega.$ Puhtaasti imaginääristen juurten kaava antaa tulokseksi $\red x(\green t)=K_1\cos(\blue\omega \green t)+K_2\sin(\blue\omega \green t)$ Tämä voidaan trigonometristen kaavojen avulla kirjoittaa muotoon $\red x(\green t)=A\sin(\blue\omega \green t-\delta),$ missä eli amplitudi ja vaihe $\delta$ ovat tuntemattomia vakioita. Nämä voidaan määrätä alkuarvoilla.

Sovellus 2: Vaimennettu harmoninen värähtelijä

Lisätään harmoniseen värähtelijäämme nopeuteen verrannollinen vastusvoima F_v=bv. Tällöin kappaleeseen vaikuttava voima on F+F_v=-kx-bv=ma. Korvaamalla nopeus paikan aikaderivaatalla ja kiihtyvyys paikan toisella aikaderivaatalla saadaan VLHDY $m\red x''(\green t)+b \red x'(\green t)+k\red x(\green t)=0.$ Tämän karakteristinen yhtälö on mr^2+br+k=0, jonka juuret ovat $r=\frac{-b\pm\sqrt{b^2-4mk}}{2m}.$ Termi b^2-4mk määrää ovatko juuret imaginäärisiä. Karakteristisen yhtälön reaalisilla juurilla differentiaaliyhtälön ratkaisu muistuttaa eksponenttifunktiota eikä oikein värähtele. Imaginäärisillä juurilla saamme vaimenevan värähtelijän, jonka amplitudi pienenee eksponentiaalisesti (eli värähdyksen suuruus puoliintuu tasaisin väliajoin).

Vaimennetun harmonisen värähtelijän kuvaaja

Tällä geogebralla voit tarkastella vaimennetun värähtelijän kuvaajia eri massalla m, vaimennuskertoimella b ja jousivakiolla k. Voit myös siirtää lähtöarvoa raahaamalla pistettä A. Kuvaajan väri riippuu värähtelyn tyypistä, alivaimennetun värähtelijän kuvaaja on sininen, kriittisesti vaimennetun violetti ja ylivaimennetun punainen. Kuvaaja kertoo heilurin poikkeaman suuruuden (pystyakseli) ajanhetkellä t (vaaka-akseli).

Mutta miksi ratkaisukaavat toimivat?

Ratkaisukaavojen todistamiseksi riittäisi osoittaa, että funktio y(x) toteuttaa annetun DY:n ja muodostuu kahdesta lineaarisesti riippumattomasta ratkaisusta. Tämä perustuu seuraavaan lauseeseen:

Jos y_1=y_1(x) ja y_2=y_2(x) ovat lineaarisen homogeenisen yhtälön A(x)y'' +B(x)y'+C(x)=0 lineaarisesti riippumattomia ratkaisuja,
niin yhtälön yleinen ratkaisu on $y= K_1y_1(x)+ K_2y_2(x), \quad K_1, K_2 \in \mathbb{R}$ ja se kattaa kaikki ratkaisut. Tällöin sanotaan, että funktiot ja muodostavat yhtälön ratkaisukannan. Vilkaistaan vielä kuitenkin miten ratkaisukaavoihin voisi päätyä.

Tutkitaan VLHDY:tä Ay''(x)+By(x)+Cy(x)=0 ja tehdään tähän sijoitukset $\begin{align*} y(x) &= e^{\red rx},\\ y'(x) &= \red re^{\red rx}=\red ry(x),\\ y''(x) &= \red r^2e^{\red rx}=\red r^2y(x). \end{align*}$ Tässä $\red r$ on tuntematon, mahdollisesti kompleksinen vakio. Alkuperäinen DY saadaan näin muotoon $y(x)(A\red r^2+B\red r+C)=0,$ josta voidaan lukea karakteristinen yhtälö.

Koska eksponenttifunktiolla $y(x)=e^{rx}$ ei ole nollakohtia, saadaan kaikki yhtälön ratkaisut karakteristisen yhtälön ratkaisuista eli juurista. Jos juuret ovat erisuuret r_1 ja r_2 saamme kaksi lineaarisesti riippumatonta funktiota $e^{r_1x}$ ja $e^{r_2x}$ , jotka toteuttavat alkuperäisen differentiaaliyhtälön ja muodostavat näin ratkaisukannan. Juurten ollessa kompleksisia saadaan reaaliset ratkaisut exponenttifunktioista pienellä pyörittelyllä. Kaksinkertaisen juuren tapauksessa saisimme vain yhden ratkaisun ja ratkaisukannan toinen funktio pitäisi tällöin löytää jollakin toisella tavalla.

VLDY:n erikoisratkaisu

Vakiokertoiminen lineaarinen (VL) toisen kertaluvun DY on epähomogeeninen (E), jos siinä esiintyy funktiosta $\red y(\green x)$ ja sen derivaatoista riippumaton termi $\blue f(\green x)$ . Tämän yleinen muoto on $a\red y''(\green x)+b\red y'(\green x)+c\red y(\green{x})=\blue f(\green x).$ Esimerkiksi $\red y'(\green x) = \blue 3 \green x$ on epähomogeeninen DY, jossa $\blue f(\green x)=\blue 3 \green x$ .

VLEDY voidaan ratkaista seuraavasti:

ratkaistaan homogeeniosaVLEDY, josta poistettu termi , VLHDY
etsitään yksi erikoisratkaisu.

Kaikki ratkaisut saadaan homogeeniosan ratkaisun ja erikoisratkaisun summana.

Todistus

Olkoon $\blue y_h=K_1\blue y_1+K_2\blue y_2$ VLHDY:n $a\blue y''+b\blue y'+c\blue y=0$ täydellinen ratkaisu ja $\red y_e$ VLEDY:n $a\red y''+b\red y'+c\red y=f(\green x)$ jokin ratkaisu. Tällöin $\violet y$ on VLEDY:n ratkaisu jos ja vain jos $\violet y=\red y_e+K_1\blue y_1+K_2\blue y_2=\red y_e+\blue y_h$ " $\Leftarrow$ " $\violet y=\red y_e+\blue y_h$ on VLEDY:n ratkaisu.

Todistus: Sijoittamalla nähdään, että $\begin{align*} a\violet y''+b\violet y'+c\violet y&=a(\red y_e''+\blue y_h'')+b(\red y_e'+\blue y_h')+c(\red y_e+\blue y_h)\\ &=a\red y_e''+b\red y_e'+c\red y_e+a\blue y_h''+b\blue y_h'+c\blue y_h\\ &=f(\green x)+0. \end{align*}$ " $\Rightarrow$ " Jos $\violet y$ on VLEDY:n ratkaisu, niin $\violet y=\red y_e+\blue y_h$ joillakin K_1 ja K_2.

Todistus: tällöin $\violet y-\red y_e$ on VLHDY:n $a\blue y''+b\blue y'+c\blue y=0$ ratkaisu (tämän voi tarkistaa sijoittamalla). Koska $\blue y_h$ on VLHDY:n täydellinen ratkaisu, on olemassa vakiot K_1 ja K_2 siten, että $\violet y-\red y_e=\blue y_h,$ eli $\violet y=\red y_e+\blue y_h.\square$

Usein helpoin tapa erikoisratkaisun löytämiseen on määräämättömien kertoimien menetelmä, jossa arvataan erikoisratkaisun muoto mutta jätetään kertoimet avoimiksi. Sijoittamalla saadaan yhtälöryhmä, josta voidaan ratkaista oikeat kertoimet.

Jos funktiosta $\red y(\green x)$ riippumaton termi on $\blue f(\green x),$ voidaan sitä vastaava yrite $\red y_e(\green x)$ valita termin $\blue f(\green x)$ mukaan:

Lisäksi:

Jos $\blue f (\green x)$ on kerrottuna $\bold n$ -asteisella polynomilla, korvataan yritteessä $\red y_e(\green x)$ olevat vapaat kertoimet ja samanasteisilla polynomeilla vapain kertoimin.
Jos $\blue f (\green x)$ on kerrottuna eksponenttitekijällä $e^{ \blue k\green x}$ , kerrotaan myös yrite $\red y_e(\green x)$ tällä tekijällä.
Jos yrite $\red y_e(\green x)$ on homogeenisen yhtälön ratkaisu, kerrotaan yrite tekijällä $\green x$ tai, jos tämäkin on HY:n ratkaisu, tekijällä $\green {x^2}$ , jne.

Yritteen valinnan jälkeen voidaan sijoittamalla kokeilla, onko se DY:n erikoisratkaisu.

Esimerkkejä arvauksista

Tässä muutama esimerkki arvauksista, jotka johtavat erikoisratkaisuun.

Kun $\blue {f(x)}=\blue{ e^{3x}}$ ja DY on

$\red y''(\green x)+2\red y'(\green x)+\red y(\green x)=\blue{ e^{3x}},$
- yrite $A\blue{ e^{3x}}$ johtaa ratkaisuun $\red y_e(\green x)=\frac{1}{16}\blue{ e^{3x}}.$

toisaalta DY:hyn

$\red y''(\green x)-7\red y'(\green x)+12 \red y(\green x)=\blue{ e^{3x}},$
- yrite $A\blue{ e^{3x}}$ ei johda ratkaisuun, koska se on homogeeniosan ratkaisu,
- yritteellä $\green x\blue{ e^{3x}}$ saadaan ratkaisu $\red y_e(\green x)=-\green x\blue{ e^{3x}}.$

Kun $\blue {f(x)}$ on polynomi, esimerkiksi DY:hyn

$\red y''(\green x)-7\red y'(\green x)+12\red y(\green x)=\blue{x^2}$
- yrite $A\blue {x^2}+B\green x+C$ johtaa ratkaisuun $\red y_e(\green x)=\frac{1}{12}\blue{ x^2}+\frac{7}{72}\green x+\frac{37}{864}.$

Miksi ratkaisuja arvaillaan?

Kaksi opiskelijaa keskustelevat:

-- Miten voi olla mahdollista, että arvaaminen on järkevä yhtälön ratkaisutapa?

-- Minusta nämä differentiaaliyhtälöt ovat aika vaikeita. Arvaaminen on järkevää, jos sillä voi oikaista pidemmän ratkaisuprosessin.

-- Mutta arvaaminenhan on tuuripeliä! Eikö olisi tehokkaampaa vain yrittää ratkaista yhtälö?

-- No joo, summamutikassa arvaaminen ei ole tehokasta, mutta valistunut arvaaminen on nopea ratkaisukeino. Suhteellisen helppojakin yhtälöitä on vaivalloista ratkaista juurta jaksaen.

-- No mikä sitten on se valistunut arvaus?

-- Niin, ja mikä on helppo yhtälö? Valistuneelle yhtälö on helppo, kun siinä on jotain tuttua. Tutut piirteet ohjaavat hyviin arvauksiin.

-- Eli jos yhtälötyypit ovat tuttuja, niin osaa arvata, että ratkaisu voisi olla tietynlainen?

-- Juuri niin. Monet differentiaaliyhtälöt ovat hyvin samankaltaisia. Yhtälöitä täytyy vain oppia lukemaan.

Arvaaminen voi tuntua epämääräiseltä ja vaikealta. Arvaaminen perustuukin siihen, että yhtälöissä on jotain tuttua. Arvaamalla ei myöskään haeta suoraan yhtälön ratkaisua, vaan ratkaisun muotoa. Varsinainen ratkaisu selviää sijoittamisen kautta.

Yhtälöitä täytyy osata lukea ja ymmärtää, jotta arvaaminen olisi järkevää. Koska ratkaisut ovat funktiota ja DY:t kuvaavat niiden käyttäytymistä, on myös funktioiden käyttäytymisen tunteminen oleellista. Kaiken tämän oppiminen ei ole helppoa, siksi differentiaaliyhtälöt ovat vaikeita.

Onneksi DY:n ratkaisuissa esiintyy usein samat funktiot eri muodoissa: erityisesti polynomit ja eksponenttifunktiot. Myös logaritmit ja trigonometriset funktiot esiintyvät usein, ja ovatkin läheisesti yhteydessä eksponenttifunktioon: logaritmi on sen käänteisfunktio, ja sini ja kosini voidaan ilmaista sen avulla.

Ratkaisut eivät aina ole yksinkertaisia, mutta näitä summaamalla ja kertomalla pääsee pitkälle.

Esimerkki

Esimerkki: Epähomogeeninen DY $y''(x)+2y(x)=\red{ x^{2}}+\green{3}$

Nyt $f(x) = \red{x^2}+\green 3,$ joten etsitään erikoisratkaisu DY:lle yriteellä $y_e(x)=\red {Ax^2}+\blue {Bx}+\green C$ . Tällöin $y_e''(x)=\green {2A}.$ Sijoittamalla nämä DY:hyn saadaan $y_e''(x)+2y_e(x)=\green{2A}+2(\red {Ax^2}+\blue {Bx}+\green C)=\red{x^2}+\green3.$ yritteen kertoimille saadaan tästä yhtälöryhmä $\begin{cases} \red {2Ax^2}=\red{x^2} \\ \blue {Bx} = \blue{0} \\ \green{2A+2C}=\green{3}. \end{cases}$ Yhtälöryhmän ratkaisut ovat $\red A=\red{\frac{1}{2}},$ $\blue B = \blue 0$ ja $\green C=\green 1$ . Yhtälön erikoisratkaisu on siis $y_e(x)=\red {\frac{1}{2}x^2}+\green {1}.$ Liittämällä tähän homogeeniosan $\red y''(x)+2\red y(x)=0$ ratkaisu $\red y_h(\green x)=K_1\cos(\sqrt2\green x)+K_2\sin(\sqrt2 \green x),$ saadaan differentiaalyhtälön ratkaisu $\begin{aligned} \red y(\green x)&= \red y_e(\green x)+\red y_h(\green x) \\ &=\frac{1}{2}\green x^2+1+K_1\cos(\sqrt2\green x)+K_2\sin(\sqrt2\green x). \end{aligned}$

Sovelluksia

Sovellus 1: Pakotettu värähtelijä

Lisätään värähtelijään kosinimuotoinen ajasta riippuva voima. Paikkaa $\red {x}(\green t)$ kuvaava differentiaaliyhtälö, eli liikeyhtälö on tällöin $\red x''(\green t)+2\beta \red x'(\green t)+ \omega_0^2\red {x}(\green t) = K\cos( \omega\green t),$ missä $\beta,$ $\omega_0$ ja $\omega$ ovat vakioita. Nyt $f(\green t)$ on kosinifunktio, joten kokeillaan ratkaisuksi $\red {x}_e(\green t)=A\sin( \omega\green t)+B\cos( \omega\green t).$ Tämän derivaatat ovat $\begin{align*} \red {x}_e'(\green t)&=A \omega\cos( \omega\green t)-B \omega\sin( \omega \green t) \\ \red {x}_e''(\green t)&=-A \omega^2\sin( \omega\green t)-B \omega^2\cos( \omega\green t ). \end{align*}$ Kun sijoitetaan $\red {x}_e(\green t)$ ja $\red {x}_e''(\green t)$ liikeyhtälöön, nähdään, että oikealla puolella on vain kosini. Sinin kertoimien summan täytyy siis olla

Termien $\sin(\omega\green t)$ ja $\cos(\omega\green t)$ kertoimista saadaan yhtälöpari $\begin{cases} ({-A \omega^2-2\beta B \omega +\omega_0^2A})= 0\\ ({-B} \omega^2+{2\beta A\omega} + \omega_0^2 B)= K. \end{cases}$ Näistä saadaan järjestelemällä $\begin{cases} ( \omega_0^2- \omega^2) A={2\beta B} \omega\\ ( \omega_0^2- \omega^2) B+ {2\beta A} \omega= K. \end{cases}$ Tästä voidaan ratkaista kertoimet ja $\begin{cases} A=\dfrac{K2\beta \omega}{(\omega_0^2- \omega^2)^2+(2\beta \omega)^2}\\ {B=\dfrac{K( \omega_0^2- \omega^2)}{( \omega_0^2- \omega^2)^2+(2\beta \omega)^2}}. \end{cases}$ DY:n ratkaisu saadaan sijoitamalla nämä yritteeseen. Ratkaisun sieventämiseen voidaan käyttää sinin ja kosinin summan kaavaa $A\sin( \omega\green t)+ B\cos( \omega\green t)=C\cos( \omega\green t-\phi),$ missä $\begin{cases} C = { \pm\sqrt{ A^2+ B^2}}\\ \phi=\arctan\big(\frac{ A}{ B}\big). \end{cases}$ Vakion etumerkki on sama kuin vakion . Oletetaan ne positiivisiksi. Sijoittamalla muuntokaavaan saadut arvot vakioille ja saadaan yhtälön erikoisratkaisuksi $\begin{cases} \red {x}_e(\green t)=C\cos( \omega\green t-\phi)\\ C={\dfrac{K}{\sqrt{( \omega_0^2+ \omega^2)^2+(2\beta \omega)^2}}}\\ \phi=\arctan\left(\dfrac{2\beta \omega}{ \omega_0^2+ \omega^2}\right). \end{cases}$

Pakotettu värähtelijä visuaalisesti (GeoGebra)

Tässä voit kokeilla kuinka pakottava voima vaikuttaa värähtelijään, jonka ominaisvärähtelytaajuus on 8. Säädettävät muuttujat ovat

värähtelyn vaimennuskerroin
pakottavan voiman taajuus
pakottavan voiman amplitudi

Arvoilla b=0.2,T=3,F=20 näet, kuinka ajava voima dominoi ajan kuluessa. Kasvattamalla $T\text{:n}$ arvoa näet myös kuinka lopullinen amplitudi kasvaa lähellä värähtelijän ominaistaajuutta.

Sovellus 2: Kappale kallistuvalla tasolla

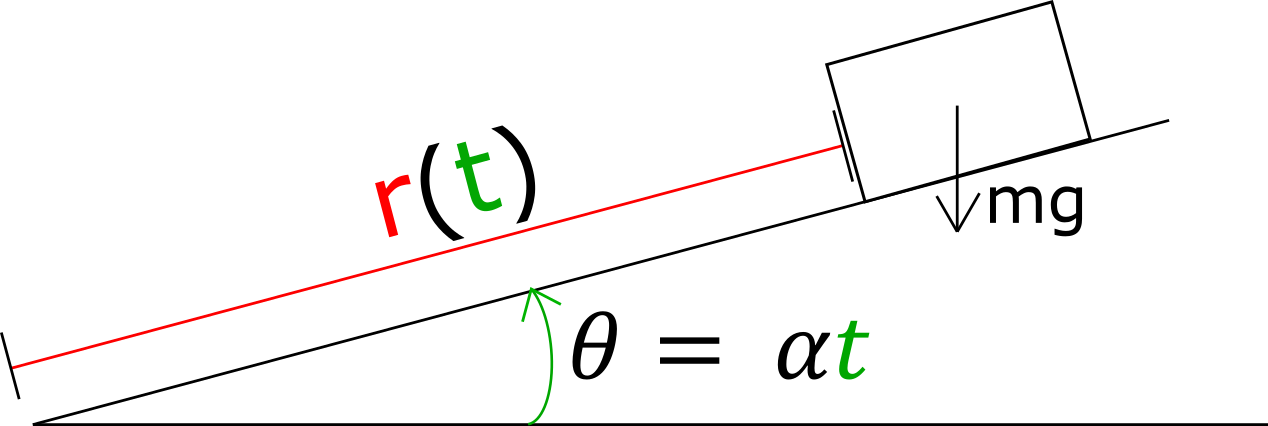
Kappale liikkuu kitkattomasti kaltevalla tasolla, jonka kaltevuuskulma $\theta$ kasvaa ajan $\green t$ mukana. Kappaleen etäisyyttä kallistuspisteestä kuvaa funktio $\red r(\green t).$ Tälle saadaan muotoiltua DY $\red r''(\green t)-\alpha^2\red r(\green t)+ \blue g\,\blue\sin(\blue\alpha \green t)=0,$ missä $\blue g$ on putoamiskiihtyvyys ja $\blue \alpha$ on tason kallistusnopeus.

Nyt $\blue f(\green t) = \blue g\,\blue\sin(\blue\alpha \green t),$ joten valitaan yritteeksi $\red r_e(\green t)= A\,\sin(\alpha \green t)+ B\,\cos(\blue \alpha \green t).$ Tällä saadaan $\begin{cases} \red r_e(\green t)= A\,\sin(\blue\alpha \green t)+ B\,\cos(\blue \alpha \green t)\\ \red r_e'(\green t)= A\,\blue\alpha\,\cos(\blue \alpha \green t) {-B}\,\blue\alpha\,\sin(\blue\alpha \green t)\\ \red r_e''(\green t)={-A}\,\blue\alpha^2\sin(\blue\alpha \green t)-{ B\,\blue\alpha^2}\cos(\blue \alpha \green t).\\ \end{cases}$ Sijoittamalla $\red r_e''(\green t)$ DY:hyn saadaan yhtälöpari $\begin{cases} \sin(\blue\alpha \green t)({-A\,\blue\alpha^2-A\blue\alpha^2+\blue g})= 0\\ \cos(\blue \alpha \green t)({-B\,\blue\alpha^2-B\,\blue\alpha^2})= 0. \end{cases}$ Tämä toteutuu kaikilla $\green t,$ kun $\begin{cases} A=\dfrac{\blue g}{2\blue \alpha^2}\\ B= 0. \end{cases}$ Erikoisratkaisu on siis $\red r_e(\green t)={\frac{\blue g}{2\blue \alpha^2}}\sin(\blue\alpha \green t).$ Koska vastaavan VLHDY:n $\red r''(\green t)-\alpha^2\red r(\green t)=0$ ratkaisu $\red r_h(\green t)$ on $\red r_h(\green t)=K_1e^{\blue\alpha \green t}+K_2e^{-\blue\alpha \green t}$ saadaan yleiseksi ratkaisuksi $\red r(\green t)=\red r_h(\green t)+\red r_e(\green t) =K_1e^{\blue\alpha \green t}+K_2e^{-\blue\alpha \green t}+ {\frac{g}{2\blue\alpha^2}}\sin(\blue\alpha \green t).$