Johdanto
Mitä on rinnakkaislaskenta
- Rinnakkaislaskennassa laskentatehtävä ratkaistaan samanaikasesti useammalla laskentayksiköllä
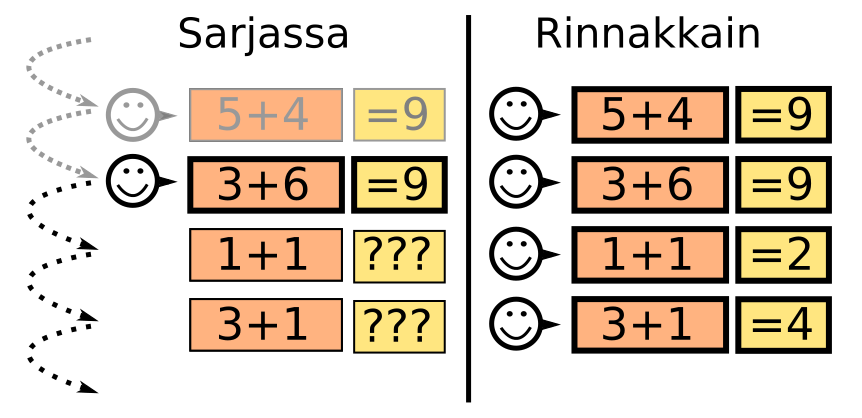
Miksi tehdä asioita rinnakkain?
- Säästetään seinäkelloaikaa
- Kierretään yksittäisen tietokoneen rajoitukset
- Voidaan tehdä monta asiaa samanaikaisesti
- Voidaan hyödyntää hajautettuja laskentaresursseja
Motivaatiota kurssin suorittamiseen
Lähdetään etsimään motivaatiota kurssin suorittamiseen seuraavasta ohjelmanpätkästä:
- Ohjelmanpätkästä löytyvä process-aliohjelma ottaa argumenttinaan taulukon
bja laskee kullekkinb:n alkiolle käänteisluvun käyttäen neljää Newtonin iteraatiota. Lopputulokset tallennetaana-taulukkoon.
void process(double *a, const double *b, int n) {
#pragma omp parallel for
for(int i = 0; i < n; i++) {
const double md = -b[i];
double y = (48.0/17.0) + (32.0/17.0) * md;
y = y + y * (1.0 + md * y);
y = y + y * (1.0 + md * y);
y = y + y * (1.0 + md * y);
y = y + y * (1.0 + md * y);
a[i] = y;
}
}- Pääohjelmassa
process-aliohjelmaa kutsutaan seuraavasti:
#define N (32*1024*1024)
// .......................
double *a = new double[N];
double *b = new double[N];
for(int i = 0; i < N; i++)
b[i] = 0.5 + 0.5*i/N;
process(a, b, N);
// .......................
delete [] a;
delete [] b;- Ohjelman CPU-version tulostus tietokoneella, jonka uumenista löytyy kaksi 6-ytimistä Intel Xeon CPU E5-2630 v2 -prosessoria:
Time: 0.0456872 s
Flops: 13.9543 GFlops
Max error: 2.22045e-16- Noin 34 miljoonan käänteisluvun laskemiseen kului Newtonin menetelmällä noin 46 millisekuntia.
- Koska kunkin käänteisluvun laskemiseen tarvitaan yhteensä 19 liukulukuoperaatiota (9 yhteenlaskua, 9 kertolaskua ja vastaluvun laskeminen), saimme prosessoreista irti hieman vajaat 14 miljardia liukulukuoperaatiota sekunnissa (14 GFlops).
Tarkastellaan seuraavaksi CUDA:lla toteutettua versiota samasta numeerisesta algoritmistä. Ohjelmakoodin yksityiskohtia ei tarvitse vielä tässä vaiheessa ymmärtää sillä niihin palataan myöhemmin:
- __global__ -avainsana kertoo, että aliohjelma voidaan suorittaa CPU:lla ja GPU:lla
- Jokaiselle säikeelle lasketaan yksikäsitteinen indeksinumero
threadIdja säikeiden määrä tallennetaanthreadCount-muuttujaan
__global__ void process(double *a, const double *b, int n) {
int threadId = blockIdx.x * blockDim.x + threadIdx.x;
int threadCount = gridDim.x * blockDim.x;
for(int i = threadId; i < n; i += threadCount) {
const double md = -b[i];
double y = (48.0/17.0) + (32.0/17.0) * md;
y = y + y * (1.0 + md * y);
y = y + y * (1.0 + md * y);
y = y + y * (1.0 + md * y);
y = y + y * (1.0 + md * y);
a[i] = y;
}
}- Pääohjelmassa process-aliohjelmaa kutsutaan seuraavasti:
double *a = new double[N];
double *b = new double[N];
...
double *d_a, *d_b;
cudaMalloc((void **)&d_a, N*sizeof(double));
cudaMalloc((void **)&d_b, N*sizeof(double));
cudaMemcpy(d_b, b, N*sizeof(double), cudaMemcpyHostToDevice);
...
// Käynnistetään noin miljoona säiettä GPU:lla
process<<<1024, 1024>>>(d_a, d_b, N);
...
cudaMemcpy(a, d_a, N*sizeof(double), cudaMemcpyDeviceToHost);- Ohjelman tulostus tietokoneella, jonka uumenista löytyy Nvidian Tesla K40c -näytönohjain:
Time: 0.00306797 s
Flops: 207.803 GFlops
Max err: 2.22045e-16- Tällä kertaa saimme laskettua samat 34 miljoonaa käänteislukua hieman reilussa kolmessa millisekunnissa.
- Kyseinen GPU on siis lähes 15 kertaa nopeampi kuin edellä mainitut Xeon-prosessorit.
Terminologiaa
Flynnin klassinen taksonomia
- Flynnin taksonomia luokittelee tietokoneet / prosessorit neljään ryhmään:
| D\I | Single Instruction | Multiple Instruction |
|---|---|---|
| Single Data | SISD | MISD |
| Multiple Data | SIMD | MIMD |
Single Instruction, Single Data (SISD)
- Yksi käskyvirta / jono järjestyksessä suoritettavia komentoja (deterministinen)
- Yksi prosessointielementti suorittaa yhden komennon kerrallaan
- Prosessointielementti operoi yksittäistä tietovirtaa / data-alkiota
- Esimerkiksi vanha PC (ei ihan)
Single Instruction, Multiple Data (SIMD)
- Yksi käskyvirta
- Useampi prosessointielementti suorittaa samanaikaisesti saman komennon
- Eri prosessointielementit voivat operoida eri tietovirtoja
- Esimerkiksi vektoriprosessorit (ja useat GPU:t)
Multiple Instruction, Multiple Data (MIMD)
- Useampi käskyvirta (mahdollisesti epädeterministinen)
- Useampi prosessointielementti, joista jokainen voi suorittaa eri käskyvirtaa
- Eri prosessointielementit voivat operoida eri tietovirtoja
- Esimerkiksi modernit moniydinprosessorit
Multiple Instruction, Single Data (MISD)
- Useampi käskyvirta
- Useampi prosessointielementti, joista jokainen voi suorittaa eri käskyvirtaa
- Kaikki prosessointielementtit operoivat samaa tietovirtaa
- Esimerkin keksiminen hankalaa
Lisää Flynnin taksonomiasta
- Flynnin taksonomia auttaa luokittelussa, mutta ei kerro koko totuutta
- Modernit suoritinytimet osaavat suorittaa useamman komennon saman kellojakson aikana (ei siis puhdas SIxx)
- Modernit suoritinytimet osaavat myöskin optimoida käskyvirran järjestystä
- Tärkeintä on, että suoritinydin käyttäytyy ulospäin kuten SISD
- Modernit suoritinytimet osaavat myöskin SIMD-temppuja (AVX)
Muista luokitteluja
- MIMD voidaan jakaa edelleen Single Program, Multiple Data (SPMD) ja Multiple Programs, Multiple Data (MPMD) luokkiin
- SPMD: Useampi itsenäinen prosessori suorittaa samanaikaisesti samaa ohjelmaa eri kohdista (yleisin tapaus)
- MPMD: Useammat itsenäiset prosessorit suorittavat eri ohjelmia samanaikaisesti (IMB Cell, CPU+GPU)
- Single instruction, Multiple Thread (SIMT): SIMD + multithreading; useampi säie suorittaa yhdessä samaa käskyvirtaa (Nvidian termi)
Terminologiaa
- Tehtävä (task): Loogisesti erillinen joukko laskennallisia komentoja, ohjelma tai osa ohjelmaa.
- Rinnakkainen / rinnakkaistuva tehtävä (parallel task): Tehtävä, joka voidaan suorittaa useammalla prosessorilla turvallisesti (laskenta tuottaa oikean tuloksen)
- Sarjalaskenta (serial execution): Ohjelman suorittaminen sarjamuotoisesti (yksi käsky kerrallaan)
- Rinnakkaislaskenta (parallel execution): Useammasta tehtävästä koostuvan ohjelman suorittaminen siten, että eri tehtäviä käsitellään samanaikaisesti
- Prosessi (process): Ajossa oleva ohjelma. Sisältää ohjelmakoodin, muistin ja erilaiset resurssit.
- Säie (thread): Pienin mahdollinen laskentaa suorittava yksikkö, jolla on oma tila. Säie voi siis suorittaa tehtävää. Prosessi voi koostua useasta säikeestä ja säikeet jakavat prosessin resurssit keskenään.
- Vuorotus (scheduling): Käytössä olevien resurssien (prosessoriajan) jakaminen tehtävien kesken
- Single threading: Yhdellä säikeellä tehtävä laskenta.
- Multithreading: Useammalla säikeellä tehtävä laskenta.
- Käskytason rinnakkaisuus (instruction level parallelism): Laitteistotasolla tapahtuva toisistaan riippumattomien konekäskyjen samanaikainen suoritus.
- Jaettu muisti (shared memory): Tietokonearkkitehtuuri, jossa kaikilla prosessoreilla on pääsy samaan yhteiseen muistiin. Ohjelmoijan näkökulmasta kyseessä on ohjelmointimalli, jossa jokainen rinnakkainen tehtävä näkee muistin samalla tavalla ja voi suoraan viitata mihin tahansa muistipaikkaan riippumatta muistin fyysisestä sijainnista.
- Hajautettu muisti (distributed memory): Tietokonearkkitehtuuri, jossa muisti on hajautettu siten, että prosessorilla ei välttämättä ole suoraa pääsyä kaikkeen käytössä olevaan muistiin. Ohjelmoijan näkökulmasta kyseessä on ohjelmointimalli, jossa rinnakkainen tehtävä näkee loogisesti vain osan käytössä olevasta muistista ja joutuu turvautumaan eksplisiittiseen kommunikointiin muissa tilanteissa.
- Kommunikointi (communication): Rinnakkaisten tehtävien välistä datan siirtoa kutsutaan kommunikoinniksi riippumatta siitä miten se käytännössä tapahtuu.
- Synkronointi (syncronization): Synkronointia käytetään rinnakkaisten tehtävien suoritusten koordinointiin reaaliajassa. Tyypilllisesti tehtävä saavuttaa erityisen synkronointipisteen, jossa se joutuu odottamaan muita tehtäviä.
- Prosessoriaika (cpu time, process time): Prosessorin laskentaan käyttämä aika
- Seinäkelloaika (wall clock time): Laskentaan käytetty todellinen aika
- Hienojakoisuus (granularity): Laskennan ja kommunikoinnin määrän välinen suhde
- Nopeutus (speedup): Mittaa kuinka paljon nopeammin rinnakkainen algoritmi voi ratkaista saman ongelman kuin (paras mahdollinen) sarjamuotoinen algoritmi.
- Skaalautuvuus (scalability): Laitteiston tai ohjelmiston kyky osoittaa suhteellista nopeutuksen kasvua laskentaresurssien (prosessorien) määrän kasvaessa
- Parallel overhead: Rinnakkaisten tehtävien hallintaan kuluva aika. Yleisemmin "ei oleellisten asioiden" tekemiseen kuluvat resurssit.
- Laskentasolmu (node): Hajautetut laskentaresurssit esitetään usein verkkona, jossa solmut vastaavat laskentaa suorittavia yksiköitä (esim. PC) ja linkit kommunikointiin käytettävää verkkoa. Solmu voi olla
- laiha (thin) eli sisältää suhteessa vähän laskentaresusseja tai
- paksu (fat) eli sisältää suhteessa paljon laskentaresusseja.
- Massiivisesti rinnakkainen (massively parallel): Laitteisto, joka koostuu erittäin suuresta määrästä prosessoreita.
- Latenssi (latency): Tapahtuman (esim. muistista lukeminen tai kirjoittaminen) käsittelyyn kuluva aika. Lasketaan usein (milli- tai mikro-) sekunneissa tai kellojaksoissa.
- Kaistanleveys (bandwidth): Ajanjakson aikana teoreettisesti siirrettävissä oleva tietomäärä. Lasketaan usein tavuina sekunnissa.
- I/O (Input and Output): Ohjelman syöte (data) ja tuloste (tulos). Levyltä tai verkosta lukeminen ja kirjoittaminen.
- Heterogeeninen alusta (heterogeneous platform): Laskenta-alusta, joka koostuu usean tyyppisistä laskentaa suorittavista elementeistä
- Homogeeninen alusta (homogenous platform): Laskenta-alusta, jonka kaikki laskentaa suorittavat elementit ovat samanlaisia
- Synkroninen (synchronous): Samanaikaisesti tapahtuva
- Epäsynkroninen (asynchronous): Tapahtumat voivat tapahtua eri aikoina
- Blocking: Prosessi voi olla kerrallaan vain yhdessä tilassa. Tapahtuma, joka estää muut samanaikaiset tapahtumat.
- Non-blocking: Prosessi voi olla kerralla useammassa tilassa. Tapahtumat eivät estä muita samanaikaisia tapahtumia.
- Flop: (Liukuluku)laskentaoperaatio
- Mop (Memory operation): Muistioperaatio
- Deadlock: Kaksi kilpailevaa tehtävää odottaa toistensa valmistumista, mutta kumpikaan ei saa omaa laskentaansa valmiiksi ilman toiselta tarvittavaa laskentatulosta.
- Livelock: Samankaltainen tilanne kuin deadlock, mutta tehtävien tilat vaihtelevat
- Race condition: Kaksi kilpailevaa tehtävää yrittävät käyttää samaa resurssia, mutta epäonnistuvat
Muistimallit
Jaettu muisti
- Jaetun muistin arkkitehtuureissa kaikki prosessorit jakavat samat muistiresurssit
- Yhden prosessorin tekemät muutoksen näkyvät suoraan muille prosessoreille
UMA ja NUMA
- Uniform Memory Access (UMA): Kaikki prosessorit voivat käyttää kaikkea muistia yhtä nopeasti
- Non-uniform Memory Access (NUMA): Kaikki prosessorit pääsevät suoraan käsiksi kaikkiin muistiresursseihin, mutta hakuajat riippuvat prosessorista ja muistipaikan fyysisestä sijainnista
Hyödyt
- Helppo ohjelmoida (ei eksplisiittistä kommunikointia lukuun ottamatta synkronointia)
- Tehtävien välinen kommunikointi on nopeaa
Haitat
- Ohjelmoijan tulee edelleen huolehtia siitä, että tehtävät käyttävät muistia oikein (järjestys, synkronointi, jne)
- Tehokkaan laitteiston rakentaminen on hankalaa ja kallista mikäli prosessoreita on paljon
Hajautettu muisti
- Hajautetun muistin arkkitehtuurissa jokaisella prosessilla on oma lokaali muisti
- Datan jakaminen prosessorien kesken vaatii kommunikointia verkon (tai muun vastaavan) yli
Hyödyt
- Skaalautuu helpommin
- Lokaalin muistin käyttäminen on nopeaa
- Voidaan toteuttaa normaaleilla PC-koneilla ja verkkokorteilla \(\implies\) pienet kustannukset
Haitat
- Hankalampi ohjelmoida (kommunikointi prosessorien välillä jne)
- Datan alustava jakaminen prosessorien ja niiden lokaalien muistien kesken saattaa olla haastavaa.
- Verkon kautta tapahtuva datan jakaminen on monta kertaluokkaa hitaampaa kuin lokaalin muistin suora käyttö
Hybridimuistiarkkitehtuurit
- Usein laskentaklusterit muodostuvat useista erillisistä tietokoneista, joista jokaisessa on useampi prosessori (joissa edelleen useampi ydin)
- Tietokoneen (CPU(t) + RAM) tasolla kyseessä on jaetun muistin arkkitehtuuri
- Laskentaklusterin tasolla kyseessä on hajautetun muistin järjestelmä
Rinnakkaisohjelmointimallit
Tyypillisimmät mallit
- Jaetun muistin malli
- Säiemalli
- Viestinvälitysmalli
- Hybridimalli
Yleiskatsaus malleihin
- Mallit eivät liity erityisesti tiettyn tyyppisiin laitteistoihin tai muistiarkkitehtuureihin
- Mikä tahansa malli voidaan periaatteessa toteuttaa millä tahansa laitteistolla
- Viestinvälitys jaetun muistin arkkitehtuurissa, emuloitu jaetun muistin malli hajautetun muistin arkkitehturissa, jne
- Ei voida suoraan sanoa mikä malli on paras, mutta tietyt mallit soveltuvat paremmin tietyille alustoille
- Eri mallien väillä voi olla päällekkäisyyksiä
Jaetun muistin malli
- Tehtävät jakavat yhteisen muistiavaruuden, josta ne voivat lukea ja johon ne voivat kirjoittaa
- Muistin hallinta tapahtuu semaforien ja lukkojen kautta
- Ei datan omistajuuden -käsitettä, dataa ei tarvitse eksplisiittisesti kommunikoida tehtävien välillä
Jaetun muistin malli
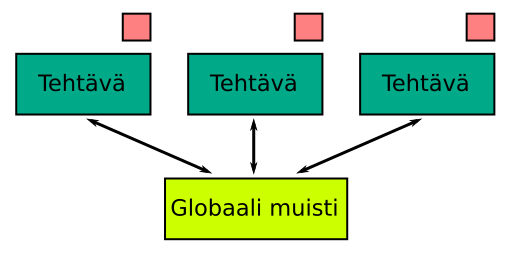
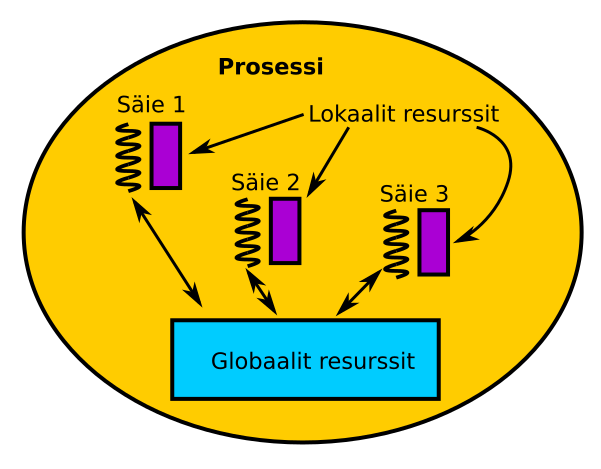
Säiemalli
- Säiemallissa yhteen prosessiin saattaa kuulua useampi säie
- Jokaisella säikeellä on oma lokaali data ja tila
- Kaikki säikeet jakavat yhteisen globaalin muistin ja kommunikoivat sen kautta
- Sykronointi on oleellisessa asemassa
Lisää säiemallista
- Säikeiden hallinta on usein halvempaa kuin erillisien prosessien hallinnointi
- Ohjelmoija määrittelee rinnakkaiset tehtävät käsin kääntäjädirektiivien ja/tai erityisien aliohjelmakutsujen avulla
- Kaksi tunnetuinta toteutusta: POSIX Threads ja OpenMP
Lisää säiemalleista
POSIX Threads (”Pthreads”)
- IEEE standardi vuodelta 1995
- Perustuu erilliseen kirjostoon, aliohjelmakutsupohjainen
- Ekplisiittistä rinnakkaisuutta, ohjelmoija määrittelee kaiken
OpenMP
- Kääntäjädirektiiveihin perustuva standardi
- Saatavilla esim. C/C++ ja Fortran kieliin
- Useissa tapauksissa sarjamuotoinen koodi voidaan (ainakin osittain) rinnakkaistaa lisäämällä muutama
#pragma omp-direktiivi
Viestinvälitysmalli
- Joukko tehtäviä, joista jokaisella on oma lokaali muisti
- Tehtävät saattavat sijaita samassa fyysisessä laitteessa tai hajautettuna useampaan laitteeseen
- Tehtävien välinen kommunikointi tapahtuu viestejä lähettämällä ja vastaanottamalla (SEND, RECEIVE)
- Perustuu tyypillisesti erilliseen kirjastoon, aliohjelmakutsupohjainen
- Ekplisiittistä rinnakkaisuutta, ohjelmoija määrittelee kaiken
- Useita standardeja
Viestinvälitysmalli
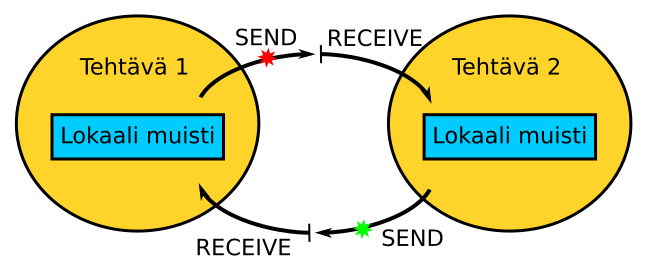
MPI
- MPI-standardista on tullut ”de facto”
- Soveltuu sekä jaetun, että hajautetun muistin arkkitehtuureille (viestin väliltys tapahtuu jaetun muistin kautta silloin kuin mahdollista)
Hybridimalli
- Eri malleja voidaan myöskin yhdistellä
- Esimerkiksi laskentaklusteri, joka koostuu useasta moniydinprossorilla varustetusta PC-koneesta
- Ylemmällä tasolla koneet kommunikoivat keskenään MPI-rajapinnan yli
- Alemmalla tasolla prosessorit / ytimet kommunikoivat keskenään OpenMP-rajapinnan yli
Rinnakkaisen ohjelmakoodin kirjoittaminen
Käy läpi seuraava lista ennen rinnakkaistamista
- Valitse numeerisesti vakaa ja tehokas algoritmi
- Tehoton tai epävakaa rinnakkainen ohjelmakoodi ei ole kenellekkään hyödyksi
- Etsi ohjelmakoodin ns. "kuumat pisteet" (hotspots)
- Tunnista rinnakkaistamista rajoittavat tekijät
- Selvitä voidaanko hotspotit rinnakkaistaa
Onko tehtävä rinnastettavissa?
Rinnakkaistuva tehtävä
- Laske sisätulo \[ x \cdot y = \sum_{i=1}^{n} x_iy_i, \; x,y \in \mathbb{R}^n \]
- Joukko \(\{1, 2, \dots, n\}\) voidaan jakaa osajoukkoihin \(M_1, M_2, \dots, M_m\), jolloin \[ x \cdot y = \sum_{j=1}^{m} \underbrace{\left( \sum_{i \in M_j} x_iy_i \right)}_{\text{Rinnakkainen tehtävä}} \]
Havainnekuva sisätulon laskemisesta rinnakkain
Ei-rinnakkaistuva tehtävä
- Laske Fibonaccin luvut \[ F_1 = 0, \\ F_2 = 1, \\ F_i = F_{i-2} + F_{i-1}, \; 3 \leq i \]
- Seuraava luku jonossa riippuu kahdesta edellisestä, tehtävä ei rinnakkaistu:
Keskity hotspotteihin
- Tunnista ohjelmakoodin hotspot'it eli koodirivit, joissa tehdään eniten töitä
- Keskity hotspot'ien rinnakkaistamiseen, unohda turha virittely
- Koodirivien määrä \(\neq\) tehtävä työ:
Hotspottien tunnistaminen
- Hotspottien löytäminen ei ole välttämättä triviaali tehtävä vaan vaatii algoritmin toiminnan syvällistä ymmärrystä
- Jos ohjelmakoodi on tuntematon, sisäkkäisten silmukoiden etsiminen on hyvä paikka aloittaa. Laske iteraatiomäärät ja arvioi iteraation hinta (kompleksisuusanalyysi):
- Erilaiset profilointityökalut ovat myöskin hyödyksi
Esimerkkejä kompleksisuusanalyysistä
- Luokkaa \(\mathcal{O}(1)\) laskentaoperaatiota:
double y = x + 7.0;- Luokkaa \(\mathcal{O}(2N) = \mathcal{O}(N)\) laskentaoperaatiota:
for(int i = 0; i < N; i++)
y[i] = 4.0 * x[i] + 7.0;- Luokkaa \(\mathcal{O}(N(1 + 2M)) = \mathcal{O}(NM)\) laskentaoperaatiota:
for(int i = 0; i < N; i++) {
x[i] = x[i] + 5.0;
for(int j = 0; j < M; j++)
y[i] = A[i][j] * x[i] + 7.8;
}Tehtävän osituksesta
- Rinnakkaisen ohjelmakoodin toteutuksessa lähdetään liikkeelle tehtävän jakamisesta osiin eli osituksesta (partition, decomposition)
- Kaksi lähestymistapaa: toiminnallinen ositus (functional decomposition) ja tilaositus (domain decomposition)
- Myöskin termit tehtävärinnakkaisuus (task parallel) ja datarinnakkaisuus (data parallel) esiintyvät usein
Toiminnallinen ositus / Tehtävärinnakaisuus
- Laskennalliset tehtävät jaetaan laskentasolmujen kesken
Tilaositus / Datarinnakaisuus
- Laskennassa käytettävä data jaetaan laskentasolmujen kesken
Tehtävärinnakaisuus vs datarinnakaisuus
- Tehtävä- ja datarinnakkaisuuden välillä sijaitsee jatkumo
- Ohjelman eri osat saattavat hyödyntää eri suhteissa tehtävä- ja datarinnakkaisuutta
Esimerkki tehtävä- ja datarinnakkaisuuden yhdistämisestä
Tarvitaanko kommunikointia aina?
- Jotkut tehtävät voidaan rinnakkaistaa ilman kommunikointia
- Termiä embarrassingly parallel viljellään paljon tässä yhteydessä
- Myöskin termi triviaalisti rinnakkaistuva on esiintynyt joissakin lähteissä
- Esimerkiksi kahden vektorin yhteenlasku \(x+y\), \[ (x + y)_i = x_i + y_i, \; i=1,\dots,n, \; x,y \in \mathbb{R}^n, \] ei vaadi kommunikointia ja on siten triviaalisti rinnakkaistuva:
Milloin kommunikointia tarvitaan?
- Usein kommunikointi on tarpeellista
- Esimerkiksi sisätulon laskeminen tarvitsee kommunikointia:
Kommunikoinnin laajuus (scope)
- Pisteestä pisteeseen -kommunikointi (point-to-point): Kaksi tehtävää kommunikoivat keskenään. Toinen tehtävistä on lähettäjä ja toinen vastaanottaja.
Kollektiivinen kommunikointi
- Kollektiivinen kommunikointi (collective): Useat tehtävät osallistuvat kommunikointiin
Synkroninen kommunikointi
- Synkroniseen kommunikointiin liittyy tyypillisesti jonkinlainen kättely (handshaking)
- Viestin vastaanottaja kuittaa viestin ja lähettäjä saa tiedon onnistuneesta siirrosta
- Kyseessä on ns. blocking-tyyppinen kommunikointi eli prosessien tulee odottaa kunnes kommunikointi on saatettu loppuun
Esimerkki synkronisesta kommunikoinnista
Asynkroninen kommunikointi
- Asynkroniseen kommunikointiin ei liity kättelyä
- Viestin lähettäjä ei odota kuittausta
- Kyseessä on ns. non-blocking-tyyppinen kommunikointi eli prosessit eivät odota kommunikoinnin loppumista
- Laskenta ja kommunikointi voivat tapahtua samanaikaisesti
- Parantaa useimmissa tilanteissa ohjelmakoodin tehokkuutta, mutta on hankalampi toteuttaa
Esimerkki asynkronisesta kommunikoinnista
Synkronointi
- Synkronointi mahdollistaa rinnakkaisien tehtävien suorituksen koordinoinnin
- Käytetään tilanteissa, joissa halutaan
- varmistua siitä, että kaikki tehtävät ovat suorittaneet jonkin toiminnon (esim. ratkaisseet osatehtävän)
- halutaan suojata jokin resurssi (esim. jaettu muistiresurssi)
Synkronointi “esteen” (barrier) avulla
- Käytetään tilanteissa, joissa halutaan varmistua siitä, että kaikki tehtävät ovat suorittaneet jonkin toiminnon
- Yleensä kaikki tehtävät osallistuvat synkronointiin
- Kaikki tehtävät tekevät töitä kunnes saavuttavat erityisen synkronointipisteen
- Tehtävät odottavat muita tehtäviä synkronointipisteessä
- Synkronointiin saattaa liittyä erityisen ohjelmakoodin suorittaminen tai tehtävät saattavat jatkaa suoritustaan normaalisti
Esimerkki synkronoinnista esteen avulla
Synkronointi lukon tai semaforin avulla
- Käytetään tyypillisesti jonkin resurssin suojaamiseen
- Synkronointiin osallistuvien tehtävien määrä voi vaihdella
- Ensimmäinen tehtävä ottaa haltuunsa lukon/semaforin. Vain yksi tehtävä voi omistaa lukon/semaforin kerrallaan
- Muiden tehtävien tulee odottaa lukon/semaforin vapautumista
- Lukko vs samafori
- Semafori asettaa tehtävät jonoon FIFO-periaatteella
- Lukon tapauksessa estetyt tehtävät yrittävät toistuvasti saada lukon käyttöönsä
Esimerkki kriittisen ohjelmakoodin suojaamisesta semaforin avulla
Synkronointi ja laitteisto
- Esteen tai lukon/semaforin avulla tapahtuva synkronointi nojaa usein laitteistotason ominaisuuksiin:
- Erillinen konekielinen synkronointikomento rautatasolla tapahtuvaan synkronointiin (esim. GPU)
- Erilliset atomiset operaatiot lukkojen ja semaforien turvalliseen käsittelyyn (normaali prosessori)
Synkronointi viestinvälityksen avulla
- Synkronointi voi tapahtua myös synkronisen viestinvälityksen avulla:
- Yksi tehtävä (master) odottaa muilta tehtäviltä synkronointipyytöä
- Muut tehtävät lähettävät synkronointipyynnön masterille ja jäävät odottamaan
- Master lähettää kuittauksen muille tehtäville saatuaan synkronointipyynnön kaikilta tehtäviltä ja jatkaa suoritustaan
- Muut tehtävät jatkavat suoritusta saatuaan kuittauksen masterilta
Latenssi ja kaistanleveys
- Latenssi on aika, joka kuluu minimaalisen viestin (0 tavua) välittämiseen, joko muistin ja prosessorin tai prosessorien välillä. Ilmoitetaan (milli- tai mikro-) sekunteina tai kellojaksoina.
- Kaistanleveys kertoo paljonko informaatiota voidaan siirtää annetun ajanjakson aikana. Ilmoitetaan usein gigatavuina sekunnissa.
- \(L\) tavun kommunikoimiseen kuluu siis \[ t = t_{lat} + L/B \] aikayksikköä, jossa \(t_{lat}\) on latenssi ja \(B\) kaistanleveys
Havainnekuva latenssin ja kaistaleveyden erosta
Laskenta vs kaistanleveys vs latenssi
- Laskenta on verrattain halpaa:
- Moderni CPU: \(\mathcal{O} (10^{10})\) Flops
- Moderni GPU: \(\mathcal{O} (10^{12})\) Flops
- Datan siirtäminen on hieman kalliimpaa:
- Ethernet: \(\mathcal{O} (10^{8})\) B/s
- RAM-muisti: \(\mathcal{O} (10^{10})\) B/s
- GPU:n videomuisti: \(\mathcal{O} (10^{11})\) B/s
Laskenta vs kaistanleveys vs latenssi (jatkuu)
- Latenssin aiheuttamat kustannukset ovat mittavat:
- Ethernet \(\mathcal{O} (10^{-3})\) sekuntia
- RAM-muisti / GPU:n videomuisti: \(\mathcal{O} (10^{-7})\) sekuntia
- GPU voisi siis (erittäin karkeasti arvioiden)
- suorittaa \(\mathcal{O}(10)\) laskentaoperaatiota yhtä siirrettyä tavua kohden
- siirtää \(\mathcal{O}(10^4)\) tavua latenssiajan aikana
- suorittaa \(\mathcal{O}(10^5)\) laskentaoperaatiota latenssiajan aikana
Laskenta vs kaistanleveys vs latenssi (jatkuu)
- On tehokkaampaa pakata useampi pieni viesti suuremman viestin sisälle ja tehdä välissä mahdollisimman paljon laskentaa:
Yhteenveto: kommunikointi on kallista
- Kellojaksoja kuluu datan odottamiseen laskennan sijasta
- Monimutkaistaa ohjelmakoodia (synkronointi jne)
- Kommunikointi saattaa estää rinnakkaistamisen käytännössä kokonaan
- Rajoittaa kääntäjän toimintaa
- Annetun ajanjakson aikana voidaan suorittaa vain rajoitettu määrä kommunikointia
Datariippuvuudet
- Ohjelman komentojen välillä on datariippuvuus silloin kun komentojen suoritusjärjestys vaikuttaa lopputulokseen
- Seuraa tyypillisesti tilanteista, joissa samaa tallennuspaikkaa käyttää useampi tehtävä
- Datariippuvuuksien ymmärtäminen on tärkeää, koska ne ovat yksi tyypillisimmistä rinnakkaistamisen estäjistä
Esimerkki datariippuvuudesta
- Laske Fibonaccin luvut \[ F_1 = 0, \\ F_2 = 1, \\ F_i = F_{i-2} + F_{i-1}, \; 3 \leq i \]
- Seuraava luku jonossa riippuu kahdesta edellisestä, tehtävä ei rinnakkaistu:
Datariipuvuuksien esittäminen graafin avulla
- Datariippuvuudet voidaan esittää kompaktissa muodossa graafirakenteen (dependency graph) avulla:
Datariipuvuuksien käsitteleminen
- Tunnista ohjelmakoodin toisistaan riippumattomat osat, ne voidaan käsitellä rinnakkain
- Datariippuvuuksia sisältävät kohdan vaativat jonkin tyyppistä synkronointia:
- Hajautetun muistin tapaus: kommunikoi data synkronointipisteissä
- Jaetun muistin tapaus: synkronoi muistin käyttö tehtävien välillä
Kuorman jakaminen
- Kuorman jakamisella (load balancing) tarkoitetaan laskentakuorman jakamista tehtävien kesken siten, että kaikki tehtävät työllistyvät
- Voidaan ajatella “tyhjäkäyntiajan” minimoimisena
- Esim. tilanne, jossa suuri joukko tehtäviä synkronoi esteen avulla. Tällöin hitain tehtävä määrää tahdin.
Kuorman jakaminen tasan tehtävien kesken
- Soveltuu tilanteisiin, joissa tehdään paljon samanlaista työtä
- Taulukko, jonka jokainen alkio käsitellään samalla tavalla
- Silmukka, jonka jokainen iteraatio on yhtä kallis
Kuorman jakaminen dynaamisesti
- Joissain tilanteissa tehtävän työn määrä saattaa vaihdella dynaamisesti tai työn jakaminen tasan on muuten mahdotonta/hankalaa
- Ratkaisuksi saattaa sopia vuorotin (scheduler) ja “työpooli”, josta työ jaetaan dynaamisesti tehtävien kesken
Parallel Overhead
- Rinnakkaistaminen aiheuttaa usein ylimääräistä työtä eli ns. parallel overhead'ia
- Pahimmassa tapauksessa parallel overhead'in määrä kasvaa kun rinnakkaisuuden määrää lisätään
- Parallel overhead'iin voi sisältyä esimerkiksi
- Tehtävien käynnistys- ja päättymisajat
- Kommunikointi ja synkronointi
- Dynaaminen kuorman jakaminen
- Käytetyn laskenta-alustan piilotetut kustannukset (käyttöjärjestelmä jne)
Havainnekuva parallel overhead'ista
Kuinka suuriin osiin tehtävä kannattaa osittaa?
- Jotkin tehtävät jakautuvat helposti moneen rinnakkaiseen osatehtävään ja toiset eivät:
- Lineaarialgebran operaatioissa voidaan usein mennä vektorin komponenttien tasolle
- Toissa tapauksissa rinnakkainen tehtävä saattaa käsittää gigatavuja dataa
- Ositus vaikuttaa kommunikoinnin määrään (tästä lisää myöhemmin)
- Datariippuvuudet
Kuinka suuriin osiin tehtävä kannattaa osittaa? (jatkuu)
- Myöskin laitteisto vaikuttaa valintoihin
- Laskentayksiköiden määrällä on suurin vaikutus. Kaikille pitäisi riittää töitä:
- Laskentasolmun koko (laiha/thin vai paksu/fat) vaikuttaa tehtävän ositukseen. Osatehtävän tulee mahtua laskentasolmun käytössä olevaan muistiin ja resussit tulisi käyttää mahdollisimman tehokkaasti
- Tarvittavan kommunikoinnin määrä vs kommunikointiresurssit
Kuinka suuriin osiin tehtävä kannattaa osittaa? (jatkuu)
- Tehtävän osituksen ja laitteiston tulisi vastata toisiaan
- Usein käytettävä algoritmi pitää vaihtaa toiseen kun laitteisto muuttuu liikaa
- Ositusta voidaan myöskin tehdä monella eri tasolla
- Laskentaklusteri / Tietokone / CPU vs GPU / GPU:n sisäinen hierarkia
Hienojakaisuus (Granularity)
- Laskennan ja kommunikoinnin määrän välinen suhde
- Suhdeluku voidaan laskea (tähän palataan myöhemmin)
- Tyypillisesti laskentaa sisältävien jaksojen välissä tapahtuu kommunikointia:
- Hienojakoinen (fine): Suhteellisen vähän laskentaa kommunikoinin välissä
- Karkeajakoinen (coarse): Suhteellisen paljon laskentaa kommunikoinnin välissä
Hienojakoisesta rinnakkaisuudesta
- Suhteellisen vähän laskentaa kommunikoinin välissä
- Matala laskenta / kommunikointi -suhde
- Kuorman jakaminen on helpompaa
- Kommunikointiin liittyvä parallel overhead on usein suuri \(\implies\) rinnakkaisuus ei välttämättä paranna tehokkuutta merkittävästi
- Liian hieno jako \(\implies\) kommunikoinin ja synkronoinnin hinta on liian suuri
Karkeajakoisesta rinnaisuudesta
- Suhteellisen paljon laskentaa kommunikoinnin välissä
- Korkea laskenta / kommunikointi -suhde
- Kuorman jakaminen saattaa olla hankalaa
- Vähemmän parallel overhead'ia \(\implies\) Rinnakkaistamisessa on enemmän potentiaalia.
Rinnakkaisen ohjelmakoodin analysointi
Muutamia määritelmää
- Flop: Floating-point operation, liukulukuoperaatio
- Flops: Flop/s, liukulukuoperaatiota sekunnissa
- Mop: Memory operation, muistioperaatio, luku tai kirjoitus
- Mops: Mop/s, muistioperaatiota sekunnissa
Suoritusnopeus (execution speed)
- Olkoon \(W\) tehtävän työmäärä (workload) ja \(T\) on tehtävän suoritusaika
- Tällöin suoritusnopeus on
\[ v = \frac{W}{T} \]
- Työkuormaa voidaan mitata esimerkiksi liukulukuoperaatioina (Flop), jolloin suoritusnopeuden yksikö olisi Flop/s eli Flops
Latenssi (latency)
- Latenssi määritellään suoritusnopeuden käänteislukuna: \[ L = \frac{1}{v} = \frac{T}{W} \]
- Latenssi kertoo siis paljonko työmäärän tekemiseen kuluu aikaa
Suoritusteho (throughput)
- Olkoon \(\rho\) suoritustiheys (execution density) ja \(A\) suorituskapasiteetti (execution capacity)
- Tällöin suoritusteho on
\[ Q = \rho vA = \frac{\rho AW}{T} = \frac{\rho A}{L} \]
Esimerkki suoritustehon laskemisesta
- Olkoon
- \(\rho\) = yhteen käskyyn sisältyvien liukulukuoperaatioiden määrä,
- \(v\) = yhden prosessoriytimen yhden sekunnin aikana suorittamien käskyjen määrä ja
- \(A\) = prosessoriytimien määrä.
- Tällöin
- suoritustehon yksikkö olisi Flops ja
- suoritusteho antaisi laitteiston teoreettisen laskentatehon eli montako liukulukuoperaatiota laitteisto kykenee (ideaaliolosuhteissa) suorittamaan sekunnin aikana.
Esimerkki suoritustehon laskemisesta (jatkuu)
- Tarkastellaan Nvidian Tesla K40c -näytönohjainta:
- \(\rho = 2 \frac{\text{Flop}}{\text{käsky}}\) (fused multiply–add käsky, johon sisältyy yksi kertolasku ja yksi yhteenlasku)
- \(v = 1 \frac{\text{ käsky}}{\text{kellojakso}} \times 0.745 \text{Ghz}\) (yksi käsky per kellojakso @ 0.745 Ghz)
- \(A = 15 \times 64 = 960\) (15 laskentayksikköä, joista jokaisessa 64 prosessointielementtiä / ydintä)
- Suoritustehoksi saadaan siis \[ Q = 2 \frac{\text{Flop}}{\text{käsky}} \times 1 \frac{\text{ käsky}}{\text{kellojakso}} \times 0.745 \text{Ghz} \times 690 \approx 1430 \text{ GFlops} \]
Huomautus liittyen latenssiin ja suoritustehoon
- Latessi ja suoritusteho voivat liittyä käytettyyn laitteistoon tai kehitettyyn ohjelmakoodiin
- Laitteiston tapauksessa työmäärän yksikkö on tyypillisesti Flop, Mop tai tavu
- Ohjelmiston tapauksessa työmäärän yksikkö voi olla esimerkiksi lineaarinen yhtälöryhmä tai valokuva
- Latenssi kertoisi tällöin yhtälöryhmän ratkaisemiseen tai valokuvan käsittelyyn kuluneen ajan
- Suoritusteho voisi kertoa esimerkiksi montako yhtälöryhmää voidaan ratkaista tai montako valokuvaa voidaan käsitellä sekunnissa
Nopeutus (speedup)
- Nopeutus latenssin mielessä määritellään seuraavasti: \[ S_{l} = \frac{L_1}{L_2} = \frac{T_1 W_2}{T_2 W_1}, \] jossa \(L_1\) ja \(L_2\) ovat kaksi vertailtavaa tapausta
- Nopeutus \(S_{l}\) kertoo kuinka paljon nopeampi tapaus \(L_2\) on verrattuna tapaukseen \(L_1\)
- Nopeutus \(S_{l}\) ottaa huomioon suoritusajan ja työmäärän
Rinnakkaistamiseen liittyvä nopeutus
- Yksinkertaisemmassa tapauksessa voisimme vertailla sarjamuotoisen ja rinnakkaisen toteutuksen kykyä käsitellä sama työmäärä
- Olkoon \(T_{s}\) sarjamuotoisen toteutuksen työmäärän \(W\) käsittelyyn käyttämä seinäkelloaika ja \(T_{r}\) rinnakkaisen toteutuksen saman työmäärän käsittelyyn käyttämä seinäkelloaika. Tällöin saavutettu nopeutus on \[ S_{l} = \frac{T_{s} W}{T_{r} W} = \frac{T_{s}}{T_{r}}. \]
- Nopeutus kertoo siis kuinka paljon nopeampi rinnakkainen toteutus on verrattuna sarjamuotoiseen toteutukseen. Vertailu pitää tehdä tarkastellulle alustalle parasta sarjamuotoista toteutusta käyttäen! Joskus parhaiten rinnakkaistuva algoritmi on jopa laskentamäärältään asymptoottisesti vaativampi kuin paras peräkkäinen algoritmi!
Havaittu nopeutus (Observed speedup)
- Olkoon \(w_{s}\) rinnakkaisen toteutuksen käyttämä seinäkelloaika sarjalaskennassa (suoritettu yhdellä laskentayksiköllä)
- Olkoon \(w_{rn}\) rinnakkaisen toteutuksen käyttämä seinäkelloaika rinnakkaislaskennassa (suoritettu useammalla laskentayksiköllä)
- Tällöin havaittu nopeutus on \[ S_h = \frac{w_{s}}{w_{r}} \]
- Havaittu nopeutus on ehkä suosituin nopeutusta mittaava indikaattori
Nopeutus työtehon mielessä
- Nopeutus työtehon mielessä määritellään seuraavasti: \[ S_{tt} = \frac{Q_2}{Q_1} = \frac{\rho_2 A_2 T_1 W_2}{\rho_1 A_1 T_2 W_1} = \frac{\rho_2 A_2}{\rho_1 A_1} S_l, \] jossa \(Q_1\) ja \(Q_2\) ovat kaksi vertailtavaa tapausta
- Nopeutus \(S_{tt}\) kertoo kuinka paljon nopeampi tapaus \(Q_2\) on verrattuna tapaukseen \(Q_1\)
Esimerkki suoritustehoon liittyvän nopeutuksen käytöstä
- Olkoon
- \(S_l\) = latenssiin liittyvä nopeutus kun vertaillaan alustan 1 prosessoriytimen ja alustan 2 prosessoriytimen yhden sekunnin aikana suorittamien käskyjen määrää
- \(\rho_i\) = yhteen käskyyn sisältyvien liukulukuoperaatioiden määrä alustalla \(i\)
- \(A_i\) = prosessoriytimien määrä alustassa \(i\)
- Tällöin suoritustehoon liittyvä latenssi kertoisi kuinka paljon enemmän Flop'peja alusta 2 voi käsitellä sekunnissa kuin alusta 1
Esimerkki suoritustehoon liittyvän nopeutuksen käytöstä (jatkuu)
- Tarkastellaan Nvidian GeForce GTX580 ja Tesla K40c näytönohjaimia:
- \(S_l = L_{\text{GTX580}} / L_{\text{K40c}} = \frac{0.745 \text{ Ghz}}{1/8 \times 1.544 \text{ Ghz}} \approx 3.86\) (laskennallinen arvio)
- \(\rho_{\text{GTX580}} = \rho_{\text{K40c}} = 2 \text{ Flop}/\text{käsky}\)
- \(A_{\text{GTX580}} = 16 \times 32 = 512\), \(A_{\text{K40c}} = 15 \times 64 = 960\)
- Tällöin \[ S_{tt} = \frac{2 \text{ Flop}/\text{käsky} \times 960}{2 \text{ Flop}/\text{käsky} \times 512} \times 3.86 \approx 7.2 \] eli K40c on noin 7.2 kertaa nopeampi kuin GTX580
Tehokkuus (Efficiency)
- Tarkastellaan tilannetta, jossa tehtävän suorittamiseen käytettävien resussien määrää on kasvatettu
- Olkoon \(S\) tehtävän yhteydessä esiintynyt kokonaisnopeutus (latenssi, havaittu tai työteho) ja alkoon \(s\) resurssien lisäämisestä hyötyneen tehtävän osan nopeutus (latenssi, havaittu tai työteho)
- Tällöin tehokkuus määritellään: \[ \eta = S/s \]
- Parhaassa tapauksessa \(\eta = 1 = 100\%\)
Tehokkuus rinnakkaislaskennassa
- Rinnakkaislaskennan tapauksessa voidaan tarkastella \(N\):n prosessoriytimen tuomaa tehokkuutta
- Oletaan, että \(s = N\) (rinnakkaistamisesta hyötyvän osan tehokkuus on 100%)
- Tällöin voimme määritellä prosessoriytimien määrästä riippuvan tehokkuuden: \[ \eta(N) = S(N)/N, \] jossa \(S(N)\) on \(N\):nän prosessoriytimen avulla saavutettu nopeutus verrattuna yhteen prosessoriytimeen
Superlineaarinen nopeutus
- On olemassa tilanteita, joissa \(1 < \eta\). Tällöin puhutaan superlineaarisesta nopeutuksesta.
- Esimerkkitilanne: Työmäärä jaetaan niin moneen osaan, että yhdelle rinnakkaiselle tehtävälle kuuluva data mahtuu kokonaan prosessorin välimuistiin (ja muut saman välimuistin jakavat tehtävät eivät merkittävissä määrin kilpaile samoista välimuistiriveistä). Tällöin efektiivinen muistikaista ja muistin latenssi saattavat muuttua useamman kertaluokan verran, joka johtaa nopeutuksen superlineaariseen käytökseen rinnakkaisien tehtävien funktiona.
Karkea havainnekuva superlineaarisesta käytöksestä
Amdahlin laki
- Johdetaan seuraavaksi kuuluisa Amdahlin laki, joka antaa teoreettisen (latenssiin liittyvän) nopeutuksen kun tehtävän työmäärä pysyy samana (\(W_1 = W_2 = W\))
- Olkoon \(T_1\) - resurssien kasvatusta edeltävä - tehtävän kokonaissuoritusaika ja olkoon \(p\) resurssien lisäämisestä hyötyvän osan osuus \(T_1\):stä eli \[ T_1 = (1-p)T_1 + \underbrace{p T_1}_{=: T_p}, \; 0 \leq p \leq 1 \]
Amdahlin lain johtaminen (jatkuu)
- Oletetaan seuraavaksi, että resurssien lisäämisestä hyötyvän tehtävän osan (latenssiin liittyvä) nopeutus on \(S_p\) eli \[ S_p = \frac{T_p W_p}{\hat{T}_p W_p} \iff \hat{T}_p = \frac{T_p}{S_p}, \] jossa \(W_p\) on resurssien lisäämisestä hyötyvän osan työmäärä ja \(\hat{T}\) on resurssien lisäämisestä hyötyvän tehtävän osan suoritusaika resurssien lisäämisen jälkeen
Amdahlin lain johtaminen (jatkuu)
- Nyt tiedämme, että resurssien lisäämisen jälkeinen tehtävän kokonaissuoritusaika on \[ \begin{align} T_2 &= (1-p)T_1 + \hat{T}_p = (1-p)T_1 + \frac{T_p}{S_p} \\ &= (1-p)T_1 + \frac{p T_1}{S_p} \end{align} \]
Amdahlin lain johtaminen (jatkuu)
- Koko tehtävän (latenssiin liittyväksi) nopeutukseksi saadaan siis \[ S_l = \frac{T_1 W}{T_2 W} = \frac{(1-p)T_1+pT_1}{(1-p)T_1 + \frac{pT_1}{S_p}} \]
- Sieventämällä saadaan Amdahlin laki: \[ S_l = \frac{1}{(1-p)+p/S_p} \]
Amdahlin laki rinnakkaislaskennassa
- Amdahlin laki kertoo muun muassa paljonko ohjelmakoodia voidaan potentiaalisesti nopeuttaa \(N\):n prosessoriytimen avulla
- Oletaan, että \(S_p = N\) (rinnakkaistamisesta hyötyvän osan tehokkuus on 100%)
- Tällöin \(N\):n prosessoriytimien avulla saavutettavissa oleva nopeutus on \[ S_l(N) = \frac{1}{(1-p) + p/N} \]
Amdahlin lain seuraukset
- Ensin havaitaan, että \[ S_l(S_p) = \frac{1}{(1-p)+p/S_p} \leq \frac{1}{1-p} \]
- Lisäksi \[ \lim_{N \to \infty} S_l(S_p) = \lim_{N \to \infty} \frac{1}{(1-p) + p/S_p} = \frac{1}{1-p} \]
- Suurin mahdollinen nopeutus on siis \(\frac{1}{1-p}\)
Amdahlin lain seuraukset (jatkuu)
- Amdahlin seurauksena tehokkuudeksi saadaan \[ \eta(S_p) = S_l(S_p)/S_p = \frac{1}{(1-p) S_p + p} \]
- Erityisesti \[ \lim_{S_p \to \infty} \eta(S_p) = \begin{cases} 1 &, \text{kun } p = 1 \\ 0 &, \text{kun } p < 1 \end{cases} \]
- Käytännössä \(p < 1\) eli resurssien lisäämisestä saatavat hyödyt noudattavat vähenevän tuoton lakia
Amdahlin lain käytös eri \(p\):n arvoilla
Amdahlin lain ennustaman tehokkuuden käytös eri \(p\):n arvoilla
Gustafsonin laki
- Johdetaan seuraavaksi Gustafsonin laki, joka antaa teoreettisen (latenssiin liittyvän) nopeutuksen kun tehtävän suoritusaika pysyy samana (\(T_1 = T_2 = T\))
- Olkoon \(W_1\) - resurssien kasvatusta edeltävä - tehtävän ajassa \(T\) suorittama työmäärä ja olkoon \(p\) resurssien lisäämisestä hyötyvän osan osuus \(W_1\):stä eli \[ W_1 = (1-p)W_1 + \underbrace{p W_1}_{=: W_p}, \; 0 \leq p \leq 1 \]
Gustafsonin lain johtaminen (jatkuu)
- Oletetaan seuraavaksi, että tehtävän resurssien lisäämisestä hyötyvän osan (latenssiin liittyvä) nopeutus on \(S_p\) eli \[ S_p = \frac{T_p \hat{W}_p}{T_p W_p} \iff \hat{W}_p = S_p W_p, \] jossa \(T_p\) on resurssien lisäämisestä hyötyvän osan suoritusaika ja \(\hat{W}_p\) on resurssien lisäämisestä hyötyvän osan tekemä työmäärä ajassa \(T_p\) resurssien lisäämisen jälkeen
Gustafsonin lain johtaminen (jatkuu)
- Nyt tiedämme, että resurssien lisäämisen jälkeinen tehtävän tekemä työmäärä on \[ \begin{align} W_2 &= (1-p)W_1 + \hat{W}_p = (1-p)W_1 + S_p W_p \\ &= (1-p)W_1 + S_p p W_1 \end{align} \]
Gustafsonin lain johtaminen (jatkuu)
- Koko tehtävän (latenssiin liittyväksi) nopeutukseksi saadaan siis \[ S_l = \frac{T W_2}{T W_1} = \frac{(1-p)W_1+S_p p W_1}{(1-p)W_1 + pW_1} \]
- Siventämällä saadaan Gustafsonin laki: \[ S_l = 1 - p + S_p p \]
Gustafsonin laki rinnakkaislaskennassa
- Gustafsonin laki kertoo muun muassa paljonko ohjelmakoodia voidaan potentiaalisesti nopeuttaa \(N\):n prosessoriytimen avulla
- Oletaan, että \(S_p = N\) (rinnakkaistamisesta hyötyvän osan tehokkuus on 100%)
- Tällöin \(N\):n prosessoriytimien avulla saavutettavissa oleva nopeutus on \[ S_l(N) = 1 - p + Np \]
Gustafsonin lain seuraukset
- Gustafsonin seurauksena tehokkuudeksi saadaan \[ \eta(S_p) = S_l(S_p)/S_p = \frac{1-p}{S_p} + p \]
- Erityisesti \[ p \leq \eta(S_p) \leq 1 \; \text{ ja } \; \lim_{S_p \to \infty} \eta(S_p) = p \]
Gustafsonin lain käytös eri \(p\):n arvoilla
Gustafsonin lain ennustaman tehokkuuden käytös eri \(p\):n arvoilla
Huomautus Amdahlin ja Gustafsonin lakeihin liittyen
- Amdahlin laki kertoo kuinka paljon nopeammin tehtävä voidaan ratkaista resurssien lisäämisen jälkeen. Työmäärä pysyy samana.
- Gustafsonin laki kertoo kuinka paljon enemmän tehtäviä voidaan ratkaista saman ajanjakson aikana resurssien lisäämisen jälkeen. Suoritusaika pysyy samana.
- Amdahlin ja Gustafsonin lait antavat teoreettisen ylärajan nopeutukselle, oikeassa elämässä nopeutukset ovat pienempiä!
Skaalautuvuus (scalability)
- Skaalautuvuus on ohjelmiston tai laitteiston kyky osoittaa suorituskyvyn suhteellista kasvua laskentaresurssien määrän kasvaessa: lisää tehoa \(\implies\) lisää vauhtia
- Skaalautuvuuteen vaikuttavat tekijät: algoritmin luonne, laitteisto (esim. muistikaista ja verkko), parallel overhead
- Skaalautuvuutta voidaan mitata:
- vahvalla skaalautuvuudella
- heikkolla skaalautuvuudella
Vahva skaalautuvuus (strong scalability)
- Vahvan skaalautumisen tapauksessa työmäärä pysyy samana, mutta rinnakkaisien tehtävien / prosessoriytimien määrä muuttuu
- Olkoon \(T_1\) toteutuksen käyttämä seinäkelloaika yhdellä prosessoriytimellä suoritettuna, olkoon \(N\) käytettyjen prosessoriytimien määrä ja olkoon \(T_N\) toteutuksen käyttämä seinäkelloaika \(N\):nällä prosessoriytimellä suoritettuna
- Tällöin vahva skaalautuvuus määritellään seuraavasti: \[ s_{vahva} = \frac{T_1}{N T_N} \times 100\% \]
Lisää vahvasta skaalautuvuudesta
- Amdahlin laki ja erityisesti siitä johdettu tehokkuus ennustavat vahvan skaalautuvuuden käytöstä
- Vahvaa skaalautuvuutta käytetään tyypillisesti tilanteissa, joissa laskennan hienojakoisuus on karkea ja tehtävän suoritusaika on pitkä
- Vahvan skaalautuvuuden avulla on mahdollista löytää ns. "sweet spot" eli määrä prosessoriytimiä, jolla tehtävä voidaan ratkaista nopeasti parallel overheadin määrän pysyessä edelleen mielekkäänä
Esimerkki vahvasta skaalautuvuudesta
#define N 10000000
...
void axpy(double *y, const double *x, double a, int n) {
#pragma omp parallel for
for(int i = 0; i < n; i++)
y[i] = a * x[i] + y[i];
}
...
axpy(x, y, a, N);$ for((i=1;i<=12;i++)); do OMP_NUM_THREADS=$i ./strong; done
Suoritusaika 1 säikeellä: 0.0114419
Suoritusaika 2 säikeellä: 0.00692391
Suoritusaika 3 säikeellä: 0.00632405
Suoritusaika 4 säikeellä: 0.006181
...Esimerkki vahvasta skaalautuvuudesta (jatkuu)
Heikko skaalautuvuus (weak scalability)
- Heikon skalautuvuuden tapauksessa yksittäisen prosessoriytimen tekemä työmäärä pysyy samana, mutta prosessoriytimien määrä muuttuu
- Olkoon \(T_1\) toteutuksen käyttämä seinäkelloaika yhdellä prosessoriytimellä suoritettuna ja olkoon \(T_N\) toteutuksen käyttämä seinäkelloaika \(N\):nällä prosessoriytimellä suoritettuna
- Tällöin heikko skaalautuvuus määritellään seuraavasti: \[ s_{heikko} = \frac{T_1}{T_N} \times 100\% \]
Lisää heikosta skaalautuvuudesta
- Gustafsonin laki ja erityisesti siitä johdettu tehokkuus ennustavat heikon skaalautuvuuden käytöstä
- Heikkoa skaalautuvuutta käytetään tyypillisesti tilanteissa, joissa tehtävä käyttää paljon muistia ja muita resursseja
- Ohjelmat joissa kommunikointi tapahtuu ns. lähimpien naapureiden välillä skaalautuvat yleensä hyvin heikossa mielessä, globaalia kommunikointia käyttävät taas eivät
Esimerkki heikosta skaalautuvuudesta
#define N 10000000
...
void axpy(double *y, const double *x, double a, int n) {
#pragma omp parallel for
for(int i = 0; i < n; i++)
y[i] = a * x[i] + y[i];
}
...
int n = threadCount*N; // Säikeen tekemä työ pysyy vakiona
...
axpy(x, y, a, n);$ for((i=1;i<=12;i++)); do OMP_NUM_THREADS=$i ./weak; done
Suoritusaika 1 säikeellä: 0.0115819
Suoritusaika 2 säikeellä: 0.013674
Suoritusaika 3 säikeellä: 0.0196369
Suoritusaika 4 säikeellä: 0.024848
...Esimerkki heikosta skaalautuvuudesta (jatkuu)
Roofline-malli
- Roofline-malli on analysointityökalu, joka ottaa teoreettisen laskentatehon (laskentaan liittyvä suoritusteho) lisäksi huomioon myöskin käytettävissä olevan muistikaistan (datan siirtoon liittyvä suoritusteho)
- Muistikaistan huomioon ottaminen on tärkeää erityisesti moniydinprosessorien yhteydessä sillä käytettävissä oleva muistikaista ei välttämättä kasva samassa tahdissa ytimien määrän kanssa
- Tällöin törmätään herkästi tilantaisiin, joissa saavutettu laskentateho jää kauas teoreettisesta maksimista
Lisää motivaatiota
- Esimerkiksi luentomonisteen alkupuolella esitetyssä CUDA-esimerkissä päästiin pelkästään vajaaseen 200 GFlopsin laskentatehoon vaikka Nvidian Tesla K40c -näytönohjaimen teoreettinen tuplatakkuuslaskentateho on 1430 GFlops
- Roofline-malli ennustaa saavutettavissa olevan laskentatehon \(\Lambda\)
- Malli sisältää kaksi käytettävästä laitteistosta riippuvaa ylärajaa saavutettavissa olevalle laskentateholle: \(\gamma_1\) ja \(\gamma_2\)
- Varsinainen saavutettu laskentateho \(\lambda\) mitataan empiirisesti
Operaatiointensiteetti ja laskentateho
- Roofline-malli esitetään yleensä log-log-skaalaisena pistekaaviona:
- x-akselilta löytyy ns. operaatiointensiteetti (operational intensity)
- y-akselilta löytyy laskentateho
Operaatiointensiteetti ja laskentateho (jatkuu)
- Operaatiointensiteetti (\(\tau\)) ottaa huomioon laskentakapasiteetin ja käytettävissä olevan muistikaistan
- Tarkemmiin sanottuna \(\tau\) on määritelty seuraavasti: \[ \tau = \frac{\text{laskentaoperaatioiden määrä [Flop]}}{\text{siirretty data [Byte]}} \]
Ylärajat
- Ensimmäinen yläraja on laitteiston teoreettinen laskentateho (\(\Gamma\)): \[ \gamma_1(\tau) = \Gamma \]
Ylärajat (jatkuu)
- Toinen yläraja riippuu laitteiston teoreettisesta muistikaistasta (\(\Delta\)): \[ \gamma_2(\tau) = \Delta \times \tau \]
Laitteiston tasapainopiste
- Jokaiselle laitteistolle voidaan laskea tasapainopiste (\(\Phi\)): \[ \Phi = \frac{\Gamma}{\Delta} \]
- Tasapainopiste voidaan piirtää koordinaateihin \((\Phi, \Gamma)\):
Menetelmän operaatiointensiteetti
- Numeerisen menetelmän operaatiointensiteetti (\(\upsilon\)) saadaan selville laskemalla menetelmässä esiintyneet liukulukuoperaatiot ja siirretty datamäärä
- Olkoon \(F_{count}\) ohjelman sisältyvien laskentaoperaatioiden määrä ja \(M_{bytes}\) siirretyn datan määrä tavuina. Tällöin \[ \upsilon = \frac{F_{count}}{M_{bytes}}. \]
Menetelmän operaatiointensiteetti (jatkuu)
- Kolme mahdollisuutta:
- \(\upsilon < \Phi\): Yläraja \(\gamma_2\) dominoi, menetelmä on muistikaistarajoitteinen
- \(\upsilon > \Phi\): Yläraja \(\gamma_1\) dominoi, menetelmä on laskentatehorajoitteinen
- \(\upsilon = \Phi\): Kumpikin yläraja on voimassa, menetelmä on sekä muisti- että laskentatehorajoitteinen
- Menetelmän saavutettavissa oleva laskentateho on \[ \Lambda = \min (\gamma_1(\upsilon), \gamma_2(\upsilon)) \]
Menetelmän operaatiointensiteetti (jatkuu)
- Menetelmän operaatiointensiteetti voidaan piirtää kuvaan nuolena \((\upsilon, 0) \to (\upsilon, \Lambda)\)
Menetelmän operaatiointensiteetti (jatkuu)
- Visuaalinen tulkinta:
- nuoli laitteiston tasapainopisteen vasemmalla puolella \(\implies\) muistikaistarajoitteinen
- nuoli laitteiston tasapainopisteen oikealla puolella \(\implies\) laskentatehorajoitteinen
Saavutettu laskentateho
- Saavutettu laskentateho (\(\lambda\)) mitataan empiirisesti ja piirretään kuvaajaan koordinaatteihin \((\upsilon, \lambda)\):
Saavutettu laskentateho (jatkuu)
- Helpoin tapa \(\lambda\):n laskemiseksi on mitata ohjelman suoritusaika (\(t\)), jolloin \[ \lambda = \frac{F_{count}}{t} \]
- Saavutetun laskentatehon tulisi olla lähellä saavutettavissa olevaa laskentatehoa
Miksi roofline-malli toimii?
- Laskentaa sisältävä ohjelman osuus voidaan käsitellä parhaimmassa tapauksessa ajassa \[ t_{F} = \frac{F_{count}}{\Gamma} \] ja datan siirtoa käsittelevä osuus voidaan vastaavasti käsitellä ajassa \[ t_{M} = \frac{M_{bytes}}{\Delta} \]
Miksi roofline-malli toimii? (jatkuu)
- Mikäli \(t_{F} < t_{M}\), saadaan saavutettavissa olevaksi laskentatehoksi \[ \Lambda = \frac{F_{count}}{t_{M}} = \frac{F_{count}}{M_{bytes}/\Delta} = \Delta \times \upsilon, \] joka vastaa ylärajaa \(\gamma_2\)
- Jos taas \(t_{M} < t_{F}\), saadaan saavutettavissa olevaksi laskentatehoksi \[ \Lambda = \frac{F_{count}}{T_{F}} = \frac{F_{count}}{F_{count}/\Gamma} = \Gamma, \] joka vastaa ylärajaa \(\gamma_1\)
Huomautuksia roofline-mallin liittyen
- Malliin voidaan piirtää lisää ylärajoja. Esimerkiksi:
- Erillinen yläraja tilanteissa, joissa ECC-muisti rajoittaa muistikaistaa
- Erillinen yläraja tilanteissa, joissa voidaan hyödyntää FMA-käskyä tai AVX-käskykantalaajennosta (vektorilaskentaa)
- Samaan malliin voi sisällyttää useita mittauspisteitä
- Teoreettisen laskentatehon ja muistikaistan lisäksi suorituskykyyn vaikuttavat myös monet muutkin tekijät. Tämän takia käytäntö ei välttämättä vastaa teoriaa.