Johdanto

Mitä on rinnakkaislaskenta

• Rinnakkaislaskennassa laskentatehtävä ratkaistaan samanaikasesti useammalla laskentayksiköllä

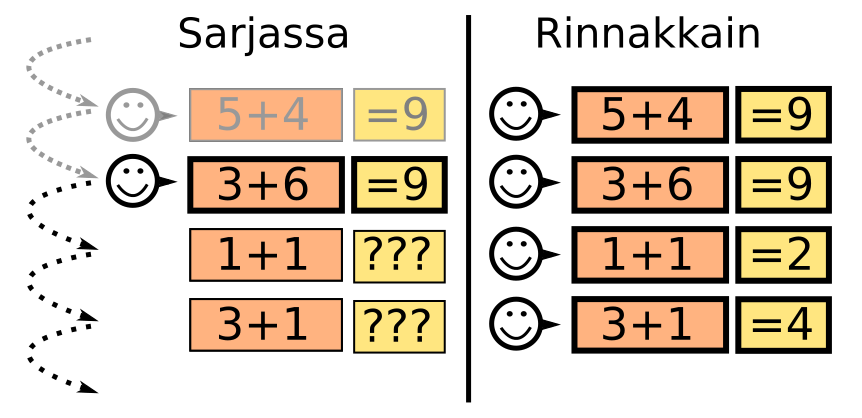
Miksi tehdä asioita rinnakkain?

• Säästetään seinäkelloaikaa
• Kierretään yksittäisen tietokoneen rajoitukset
• Voidaan tehdä monta asiaa samanaikaisesti
• Voidaan hyödyntää hajautettuja laskentaresursseja

Motivaatiota kurssin suorittamiseen

• Lähdetään etsimään motivaatiota kurssin suorittamiseen seuraavasta ohjelmanpätkästä:

  cpu-cuda-newton-esimerkki/cpu.cpp

• Ohjelmanpätkästä löytyvä process-aliohjelma ottaa argumenttinaan taulukon b ja laskee kullekkin b:n alkiolle käänteisluvun käyttäen neljää Newtonin iteraatiota. Lopputulokset tallennetaan a-taulukkoon.

void process(double *a, const double *b, int n) {
	
	#pragma omp parallel for
	for(int i = 0; i < n; i++) {

		const double md = -b[i];
		double y = (48.0/17.0) + (32.0/17.0) * md;
		
		y = y + y * (1.0 + md * y);
		y = y + y * (1.0 + md * y);
		y = y + y * (1.0 + md * y);
		y = y + y * (1.0 + md * y);
		
		a[i] = y;
	}
}

• Pääohjelmassa process-aliohjelmaa kutsutaan seuraavasti:

#define N (32*1024*1024)

// .......................

double *a = new double[N];
double *b = new double[N];

for(int i = 0; i < N; i++)
	b[i] = 0.5 + 0.5*i/N;
	
process(a, b, N);

// .......................

delete [] a; 
delete [] b;

• Ohjelman CPU-version tulostus tietokoneella, jonka uumenista löytyy kaksi 6-ytimistä Intel Xeon CPU E5-2630 v2 -prosessoria:

Time: 0.0456872 s
Flops: 13.9543 GFlops
Max error: 2.22045e-16

• Noin 34 miljoonan käänteisluvun laskemiseen kului Newtonin menetelmällä noin 46 millisekuntia.
• Koska kunkin käänteisluvun laskemiseen tarvitaan yhteensä 19 liukulukuoperaatiota (9 yhteenlaskua, 9 kertolaskua ja vastaluvun laskeminen), saimme prosessoreista irti hieman vajaat 14 miljardia liukulukuoperaatiota sekunnissa (14 GFlops).

• Tarkastellaan seuraavaksi CUDA:lla toteutettua versiota samasta numeerisesta algoritmistä. Ohjelmakoodin yksityiskohtia ei tarvitse vielä tässä vaiheessa ymmärtää sillä niihin palataan myöhemmin:

  cpu-cuda-newton-esimerkki/gpu.cu

• __global__ -avainsana kertoo, että aliohjelma voidaan suorittaa CPU:lla ja GPU:lla
• Jokaiselle säikeelle lasketaan yksikäsitteinen indeksinumero threadId ja säikeiden määrä tallennetaan threadCount-muuttujaan

__global__ void process(double *a, const double *b, int n) {

	int threadId = blockIdx.x * blockDim.x + threadIdx.x;
	int threadCount = gridDim.x * blockDim.x;
	
	for(int i = threadId; i < n; i += threadCount) {
		const double md = -b[i];
		double y = (48.0/17.0) + (32.0/17.0) * md;
		
		y = y + y * (1.0 + md * y);
		y = y + y * (1.0 + md * y);
		y = y + y * (1.0 + md * y);
		y = y + y * (1.0 + md * y);
		
		a[i] = y;
	}
}

• Pääohjelmassa process-aliohjelmaa kutsutaan seuraavasti:

double *a = new double[N];
double *b = new double[N];

...
	
double *d_a, *d_b;
cudaMalloc((void **)&d_a, N*sizeof(double));
cudaMalloc((void **)&d_b, N*sizeof(double));
	
cudaMemcpy(d_b, b, N*sizeof(double), cudaMemcpyHostToDevice);
...
// Käynnistetään noin miljoona säiettä GPU:lla
process<<<1024, 1024>>>(d_a, d_b, N);
...
cudaMemcpy(a, d_a, N*sizeof(double), cudaMemcpyDeviceToHost);

• Ohjelman tulostus tietokoneella, jonka uumenista löytyy Nvidian Tesla K40c -näytönohjain:

Time: 0.00306797 s
Flops: 207.803 GFlops
Max err: 2.22045e-16

• Tällä kertaa saimme laskettua samat 34 miljoonaa käänteislukua hieman reilussa kolmessa millisekunnissa.
• Kyseinen GPU on siis lähes 15 kertaa nopeampi kuin edellä mainitut Xeon-prosessorit.