Tämä luentomateriaali on tarkoitettu Jyväskylän yliopiston matematiikan ja tilastotieteen laitoksen kurssille
MATA114 Differentiaaliyhtälöt
(aineopinnot, 4 op). Katso kurssin käytännön järjestelyt kurssin TIM-pääsivulta.
Huom: Materiaaliin voi tulla muutoksia kurssin aikana. Myös aikatauluun voi tulla muutoksia; alustavasti 1 luku vastaa yhtä luentoa (saliopetuksessa 2x45min, etäopetuksessa yksi luentovideo).
Lähteinä on käytetty enimmäkseen seuraavia kirjoja:
[A] Adams, Robert A. Calculus: a complete course, 8. laitos, Pearson 2013
[B] Boyce, William E. ja DiPrima, Richard C. Elementary Differential Equations and Boundary Value Problems, 3. laitos, Wiley 1977
Esim. merkintä [A, x] viittaa kirjan [A] kappaleeseen x.
- : Sivun oikeassa reunassa on oransseja palkkeja niissä kohdissa, joita et ole vielä lukenut. Ne auttavat sinua näkemään lukemattomat kohdat, jos hypit tekstiä eteenpäin. Klikkaa palkkeja pois sitä mukaa kun luet materiaalia.
- Jos et halua hyödyntää tätä ominaisuutta, on vasemmalla ylhäällä ratas, jonka takaa voit klikata kaikki kappaleet kerralla luetuiksi.
- : Mikäli kappale muuttuu sen jälkeen kun olet sen lukenut, ilmestyy sen viereen keltainen palkki. Sen vieressä on painike, jolla voit tarkistaa, mitä on muuttunut.
- Kommentti: Jos jokin asia on epäselvä tai epäilet, että materiaalissa on virhe, on oikeassa reunassa C-merkki, josta voit lisätä kommentin. Kommentin voi asettaa näkymään vain itselle tai kaikille, jolloin opettaja voi lukea kommentin ja vastata siihen.
Johdattelua
Havaintoja:
Jos
, niin
eli
toteuttaa yhtälön
.
Jos
, niin
eli
toteuttaa yhtälön
.
Yhtälöitä, joissa esiintyy (tuntemattoman) funktion derivaatta tai derivaattoja, sanotaan differentiaaliyhtälöiksi.
- Usein tuntemattomasta funktiosta käytetään merkintää
tarkoittaen muuttujan
funktiota
ja sen derivaatoista vastaavasti
,
,
jne.
- Esim. yhtälö
yllä pitäisi oikeastaan kirjoittaa huolellisemmin muodossa
, mutta on tapana lyhentää merkintöjä kuten yllä.
- Esim. yhtälö
- Varsinkin sovelluksissa sekä funktio että muuttuja voidaan nimetä toisinkin; esim.
.
- Varmista, että ymmärrät merkinnät ja käytä tarvittaessa "huolellisempia merkintöjä"!
- Differentiaaliyhtälössä yhtäsuuruus (
) tarkoittaa yhtälön toteutumista "kaikilla" muuttujan arvoilla; esim. yllä jos
, niin
kaikilla
. Mitä "kaikilla" tarkoittaa, riippuu tilanteesta.
- Myös esim.
toteuttaa differentiaaliyhtälön
(tarkista itse).
- Mitä mahtavat tarkoittaa "differentiaaliyhtälön ratkaiseminen" ja "differentiaaliyhtälön ratkaisu"?
Differentiaaliyhtälön kertaluku on korkeimman yhtälössä esiintyvän derivaatan kertaluku.
- Esim.
on ensimmäisen ja
toisen kertaluvun DY.
Yleistä menetelmää kaikkien differentiaaliyhtälöiden ratkaisemiseen ei ole.
- Tällä kurssilla perehdytään muutamiin yksinkertaisimpiin ratkaisumenetelmiin, jotka soveltuvat tietyn tyyppisille differentiaaliyhtälöille, mm.
- lineaariset 1. ja osin myös 2. kertaluvun yhtälöt
- separoituvat ja separoituviksi palautuvat 1. kl:n yhtälöt
- (sekä eräitä muita yhtälötyyppejä)
- Muun tyyppisistä yhtälöistä nähdään lähinnä vain joitakin (varoittavia) esimerkkejä; mm. on olemassa hyvin yksinkertaisen näköisiä yhtälöitä, joita ei voida ratkaista analyyttisesti, tai joilla ei ole yksikäsitteistä ratkaisua annetuilla alkuehdoilla - tai ratkaisua lainkaan.
- Olemassaolo- ja yksikäsitteisyystulokset, numeeriset menetelmät, visualisointi, sarjaratkaisut, ...
- Differentiaaliyhtälösysteemillä tarkoitetaan kahden tai useamman differentiaaliyhtälön ryhmää (joka siis sisältää useita tuntemattomia funktioita derivaattoineen). Tällä kurssilla systeemeistä puhutaan hyvin vähän; aiheesta tarkemmin kiinnostuneet voivat tutustua esim. kevään 2018 kurssimateriaaliin.
Esitiedoista: tällä kurssilla
- tarvitset
- hyvät derivointi- ja integrointitaidot (esim. Calculus 3)
- alkeellisen käsityksen osittaisderivaatoista ja niiden merkinnöistä (esim. Calculus 1)
- perustiedot potenssisarjoista (esim. Calculus 3)
- on hyvä, jos olet joskus tutustunut
- kompleksilukuihin (esim. Calculus 1 tai hiukan enemmänkin)
- (Jos et, joudut "opettelemaan" asian, jonka kompleksiluvut tuntien voisit "ymmärtää".)
- kompleksilukuihin (esim. Calculus 1 tai hiukan enemmänkin)
- et varsinaisesti tarvitse
- lineaarialgebraa ennen kuin viimeisellä viikolla - ja sielläkin niukasti.
- (Toki joissakin kohdin lineaarialgebran tuntemus voi auttaa ymmärrystä.)
- lineaarialgebraa ennen kuin viimeisellä viikolla - ja sielläkin niukasti.
1. Yleistä
- käsitteitä:
- DY, kertaluku, eri muotoja
- (yksittäis)ratkaisu, yleinen ratkaisu, erikoisratkaisu
- lineaarisuus, homogeenisuus, vakiokertoimisuus
- ratkaisuksi toteaminen
- alkuehdot, alkuarvotehtävä
- ensimmäisen kertaluvun DY:n alkuarvotehtävän ratkaisun olemassaolosta ja yksikäsitteisyydestä
- sovelluksista hiukan
1.1 Käsitteitä
1.1.1 Differentiaaliyhtälö (DY)
Tavallinen differentiaaliyhtälö, usein lyhyesti vain differentiaaliyhtälö (DY), on yhtälö, joka sisältää tuntemattoman yhden muuttujan reaalifunktion ja sen derivaattoja.
Huomautuksia
- Tällä kurssilla muuttuja on aina reaalinen.
- Tuntematon funktio on siis yhden reaalimuuttujan reaaliarvoinen funktio:
,
- Älä sekoita tavallisia differentiaaliyhtälöitä, kuten esim.
yllä, ja osittaisdifferentiaaliyhtälöitä:
- Osittaisdifferentiaaliyhtälössä esiintyy tuntematon useamman kuin yhden muuttujan funktio ja sen osittaisderivaattoja.
- Esimerkiksi aaltoyhtälö
on osittaisdifferentiaaliyhtälö; funktio
riippuu (vähintään) kahdesta muuttujasta
ja
.
- Huomaa:
- differentiaaliyhtälö (DY), engl. differential equation (DE)
- yleiskäsite; voi tarkoittaa sekä tavallisia että osittaisdifferentiaaliyhtälöitä (tai sitten vain tavallisia)
- tavallinen differentiaaliyhtälö, engl. ordinary differential equation (ODE)
- osittaisdifferentiaaliyhtälö (ODY), engl. partial differential equation (PDE)
- differentiaaliyhtälö (DY), engl. differential equation (DE)
- Tällä kurssilla ei puhuta osittaisdifferentiaaliyhtälöistä. Sen sijaan osittaisderivaatan käsitettä ja merkintää tarvitaan joissain kohdin.
1.1.2 Kertaluku
Differentiaaliyhtälön kertaluku on korkeimman yhtälössä esiintyvän derivaatan kertaluku.
Esimerkkejä
on toisen kertaluvun DY
on kolmannen kertaluvun DY
Nämä yhtälöt toisin kirjoitettuina:
Huom: kun sekaannuksen vaaraa ei ole, muuttuja jätetään usein merkitsemättä kuten yllä. Usein muuttujana on tai
(aika). Lisäksi yhtälössä voi esiintyä kirjaimilla merkittyjä vakiolukuja eli parametreja.
1.1.3 Implisiittimuoto ja normaalimuoto
Ensimmäisen kertaluvun DY voidaan aina kirjoittaa muodossa .
Tätä muotoa kutsutaan implisiittimuodoksi.
- Huomaa, että mikä tahansa yhtälö voidaan aina kirjoittaa funktion avulla;
esim.on sama kuin
, kun
.
Joskus yhtälö voidaan "ratkaista" derivaatan
suhteen eli kirjoittaa muodossa
.
Tätä muotoa kutsutaan normaalimuodoksi.
- Vastaavasti
:nnen kertaluvun DY voidaan aina kirjoittaa implisiittimuodossa
ja joskus normaalimuodossa
.
- Kaikkia DY:itä ei voida kirjoittaa normaalimuodossa ja yhtä implisiittimuotoista DY:ä voi vastata useampi normaalimuotoinen yhtälö; esim.
tai
.
1.1.4 DY:n ratkaisu ja ratkaiseminen
Differentiaaliyhtälön ratkaisulla tarkoitetaan jollakin avoimella välillä
määriteltyä funktiota
, joka on vähintään
kertaa derivoituva ja jolle yhtälö
toteutuu kaikilla
.
DY:n ratkaiseminen tarkoittaa kaikkien DY:n ratkaisujen löytämistä.
Huomatuksia
- Kun halutaan korostaa, että on löydetty jokin DY:n ratkaisu, mutta ei vielä kaikkia, voidaan ratkaisusta käyttää myös nimitystä yksittäisratkaisu tai yksityisratkaisu.
- Kysymys DY:n kaikkien ratkaisujen löytämisestä ei ole helppo edes 1. kertaluvun yhtälöille. Usein ratkaisut voidaan esittää vapaan vakion avulla (vrt. integroimisvakio), mutta ei aina kaikkia, ks. esimerkki 4 alla.
- Vakion avulla annetusta ratkaisujen perheestä käytetään usein nimitystä yleinen ratkaisu.
- Lisäksi DY:llä voi olla ratkaisuja, jotka eivät kuulu yleiseen ratkaisuun; näitä kutsutaan erikoisratkaisuiksi.
Esimerkkejä
- Ratkaise
.
- Yhtälö on muotoa
, joten kaikki ratkaisut saadaan integroimalla eli antiderivoimalla:
- Ratkaise
.
- Integroimalla kerran saadaan
ja integroimalla uudestaan lopulta
- Onko
yhtälön
ratkaisu?
- Lasketaan tarpeelliset derivaatat ja tutkitaan, toteutuuko yhtälö.
ja
joten
kaikilla
, kyllä toteutuu;
siison yhtälön
(eräs) ratkaisu.
- Onko
yhtälön
ratkaisu jokaisella
? Löydätkö muita? Kulkeeko jokin ratkaisuista pisteen
kautta? Mikä?
- Koska
, niin
elion yhtälön
ratkaisu jokaisella
.
- Siis
on yhtälön
yleinen ratkaisu.
- Siis
- Lisäksi vakiofunktio
toteuttaa yhtälön.
- Koska vakiofunktiota
ei saada yleisestä ratkaisusta millään vakion
valinnalla, se on erikoisratkaisu.
- Koska vakiofunktiota
- Etsitään ne ratkaisut, jotka kulkevat pisteen
kautta eli joille
:
kun
tai
, joten
yksittäisratkaisutja
toteuttavat ehdon
.
- Ehtoa
kutsutaan alkuehdoksi; tästä lisää alla.
- Ehtoa
Huomautus
:nnen kertaluvun DY:n
yleisessä ratkaisussa esiintyy yleensä
toisistaan riippumatonta vakiota
.
1.2 Alkuarvotehtävä
Etsi se DY:n yksittäisratkaisu, joka toteuttaa annetut alkuehdot
- Alkuehtoja annetaan yleensä DY:n kertaluvun verran.
Esimerkki
- Ratkaise alkuarvotehtävä
- Yleinen ratkaisu saadaan integroimalla:
- Alkuehdon
toteutuminen:
- Alkuehdon toteuttava ratkaisu on
(Huom: Esimerkissä 5 ratkaisuväli ei voi sisältää nollaa. Löydetty funktio on alkuarvotehtävän ratkaisu välillä
.)
1.3 Teknisten apuvälineiden käytöstä
Esim. Maximalla voi ratkaista joitakin differentiaaliyhtälöitä ja alkuarvotehtäviä.
Kuvassa on esimerkin 5 alkuarvotehtävä ratkaistu Maximalla:
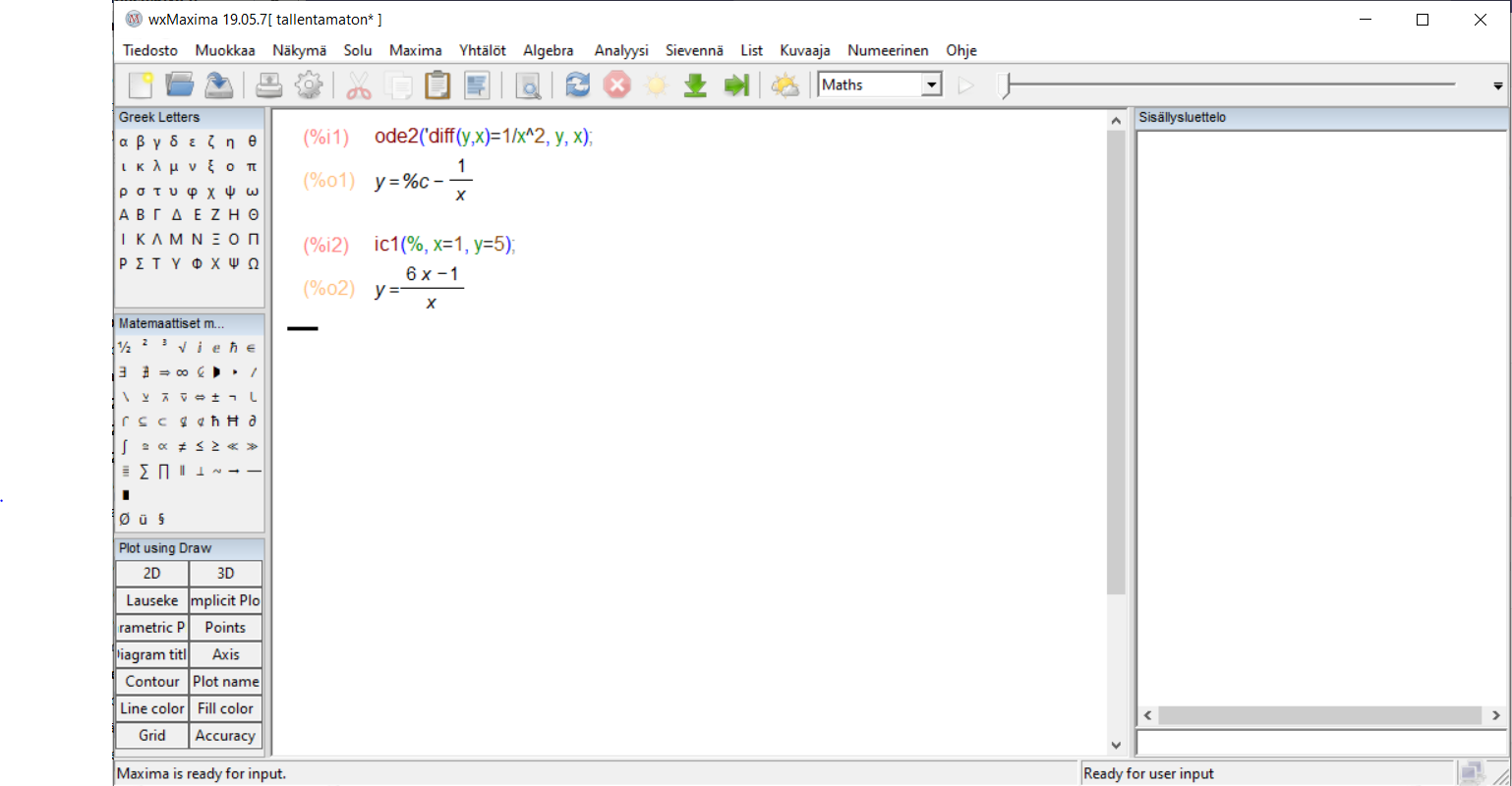
1.4 Ratkaisun olemassaolo ja yksikäsitteisyys (*)
Alkuarvotehtävällä ei välttämättä ole yksikäsitteista ratkaisua, kuten esimerkissä 4 nähtiin. Toisaalta joskus yksikäsitteinen ratkaisu löytyy, kuten esimerkissä 5. Joillakin DY:illä ei ole ratkaisua lainkaan.
Tietyillä edellytyksillä alkuarvotehtävällä on yksikäsitteinen ratkaisu. Alla oleva lause sanoo, että normaalimuotoon kirjoitetun 1. kertaluvun DY:n alkuarvotehtävällä on yksikäsitteinen ratkaisu jollakin kohdan
sisältävällä avoimella välillä, kun
on riittävän siisti.
Lause
Oletetaan, että funktiot ja
ovat jatkuvia suorakulmioalueessa, jossa
ja
, ja että piste
on suorakulmion sisällä.
Tällöin löytyy ja yksikäsitteinen välillä
määritelty derivoituva funktio
, jolle
ja
kaikilla
.
[A, s. 1000 tai B, s. 24]
Huomautuksia
- Lause siis sanoo kaksi asiaa:
- alkuarvotehtävällä on ratkaisu ("ratkaisun olemassaolo")
- ratkaisuja on vain yksi ("ratkaisun yksikäsitteisyys")
- Lauseesta seuraa mm. se, että lauseen oletukset täyttävällä differentiaaliyhtälöllä
ratkaisujen kuvaajat eivät leikkaa.
- Mieti: jos kahden eri ratkaisufunktion kuvaajat leikkaavat, funktiot saavat tässä kohdassa saman arvon eli vastaavalla alkuehdolla ratkaisuja olisi kaksi.
- Miksi esimerkin 4 havainto ei ole ristiriidassa lauseen kanssa?
- Ratkaisun olemassaolo seuraa jo funktion
jatkuvuudesta; yksikäsitteisyys vaatii enemmän.
- Lauseesta puhutaan lisää myöhemmin.
1.5 Lisää käsitteitä
1.5.1 Lineaarisuus
Jos 1. kertaluvun DY on muotoa , sitä sanotaan lineaariseksi.
Huomautuksia
- Kukin termi on siis tulo, jossa toinen tekijä on muuttujan
funktio ja toinen tuntematon funktio
tai jokin sen derivaatoista.
- Lineaarisessa DY:ssä ei esiinny esim. termejä
tai
.
- Kerroinfunktioiden
ja
ei tarvitse olla lineaarisia.
- Esim.
on lineaarinen 1. kertaluvun DY.
- Mitkä ovat kerroinfunktiot?
- Yleensä kerroinfunktioilta kuitenkin oletetaan derivoituvuus tai vähintään jatkuvuus tutkittavalla välillä.
- Esim.
Jos DY on muotoa sanomme, että DY on lineaarinen.
Jos lisäksi
kaikilla
, sanomme, että lineaarinen DY on homogeeninen;
vastaavasti, josei ole nollafunktio, lin. DY on epähomogeeninen.
Jos kerroinfunktiot
ovat vakiofunktioita, sanomme, että lineaarinen DY on vakiokertoiminen.
- Varoitus: sana "homogeeninen" on differentiaaliyhtälöidenkin yhteydessä myös toisessa käytössä (varsinkin englanninkielisissä lähteissä).
- On siis eri asia sanoa "tämä on homogeeninen DY" kuin "tämä lineaarinen DY on homogeeninen".
- Termin merkitys on varmistettava asiayhteydestä.
- Sanan toinen käyttötapa, ks. esim. [A, s. 995].
- Lineaarisista DY:istä ja niiden ratkaisemisesta puhutaan lisää myöhemmin.
- Jatkossa oletamme aina, että kerroinfunktiot
sekä funktio
ovat jatkuvia (määrittelyjoukoissaan).
1.6 Sovelluksia
Kurssilla Calculus 2 on nähty jo joitakin differentiaaliyhtälöitä sovellusten yhteydessä:
- Eksponentiaalinen kasvu / väheneminen:
- suureen kasvu- tai vähenemisnopeus on suoraan verrannollinen suureen arvoon, esim. radioaktiivinen hajoaminen
- Calculus 2, luku 5.1
- Tieto
on helppo perustella: kaikilla vakion
arvoilla funktio
on ratkaisu (ks. Calculus 2) ja toisaalta jos
, niin
eli
on vakiofunktio.
- Pian nähdään myös toinen ratkaisutapa.
- Ks. Calculus 2, 5.1.1 ja 5.1.2 esimerkkeineen.
- Tieto
- Newtonin jäähtymislaki:
- lämpötilan muutosnopeus on suoraan verrannollinen lämpötilaeroon ympäristön kanssa
- Calculus 2, luku 5.2.1
- Palautuu muuttujanvaihdolla
yhtälöksi
.
- Palautuu muuttujanvaihdolla
- Logistinen kasvu:
- suureen eksponentiaalista kasvua rajoittaa järjestelmän kantokyky, esim. populaation kasvua ravinnon määrä
- Calculus 2, luku 5.2.3
- Tästä pian lisää.
(listaa voisi vielä jatkaa)
2. Separoituva DY
- separoituva DY ja sen ratkaiseminen
- separoituvaksi palautuva DY
- käyräparven DY ja käyräparven kohtisuorat leikkaajat
[A, 7.9 ja 18.2]
2.0.1 Johdatteleva esimerkki
- Jos integroidaan yhtälö
muuttujan
suhteen, saadaan uusi yhtälö, joka on yhtäpitävä alkuperäisen kanssa:
- Jos nyt funktio
osataan integroida eli tunnetaan antiderivaatta
, voidaan jatkaa:
- Jos nyt funktio
- Huomioita:
- Integroinnissa mukaan pujahtaa vakio
, joka voi olla mikä tahansa reaaliluku.
- Integraalimerkintä sisältää kaikki antiderivaatat, joten vapaata vakiota ei tarvitse merkitä ennen kuin (viimeinen) integraalimerkki poistetaan.
- Merkinnän
avulla sama ratkaisu voidaan kirjoittaa myös näin:
- Integroinnissa mukaan pujahtaa vakio
2.1 Separoituvuus käsitteenä
Johdatteluesimerkissä differentiaaliyhtälön
- vasemmalla puolella oli yhdistetyn funktion
ja sisäfunktion
derivaatan
tulo, ja
- oikealla puolella vain muuttujan
funktio
.
Niinpä kumpikin puoli voitiin integroida.
Normaalimuodossa vastaava yhtälö olisi eli
Tämän muotoisia yhtälöitä kutsutaan separoituviksi ja yhtälön kirjottamista muotoon
"muuttujien separoinniksi" (ajatellen myös funktiota
muuttujana) eli erottamiseksi yhtälön eri puolille.
Jos ensimmäisen kertaluvun differentiaaliyhtälö voidaan esittää muodossa niin sanomme, että se on separoituva.
Huomioita ja esimerkkejä:
- myös yhtälöt
ja
ovat separoituvia (miksi?)
- yhtälö
ei ole separoituva, mutta yhtälöt
ja
ovat
- separoituva DY osataan ratkaista (ainakin melkein), jos antiderivaatat funktioille
ja
tunnetaan
- ensimmäisen kertaluvun lineaarinen homogeeninen yhtälö
ratkeaa separoimalla, ks. esimerkki myöhemmin
- tärkeää!
2.2 Esimerkkejä
(vrt. luvun 1 johdatteluosa)
- Ratkaistaan separointimenetelmällä: Jos
kaikilla
, niin saadaan
Lisäksi vakiofunktio
on ratkaisu, joten yhtälön yleinen ratkaisu on
- Huomaa, että
kaikilla
.
- Huomaa, että
- ks. myös ratkaisu päättelemällä aiemmin (kohdassa 1.6)
- Sovelluksia:
- bakteeriviljelmän kasvu, Calculus 2, 5.1.1
- radioaktiivinen hajoaminen, Calculus 2, 5.1.2
- Mallin sovittaminen:
, etsi myös tietoihin sopiva parametrin
arvo.
- Ratkaistaan separointimenetelmällä, käytetään merkintää
:
- Tätä ei voida ratkaista muotoon
(eksplisiittinen ratkaisu).
- Muotoa
tai yhtäpitävästi
kutsutaan implisiittiseksi ratkaisuksi.
- Ratkaisukäyrät ovat hyperbelejä (piirrä).
- Siis
on käyräparven
DY; tästä lisää hetken päästä.
- Tätä ei voida ratkaista muotoon
- Ratkaise alkuarvotehtävä
- Ratkaistaan DY separoimalla: selvästi vakiofunktio
on ratkaisu, mutta se ei toteuta alkuehtoa.
Alkuehdon voi toteuttaa vain
. Ratkaistaan vakio
:
Alkuehdon toteuttava ratkaisu on
- Alkuehdon
voisi sijoittaa jo kolmannen vaiheen implisiittiseen ratkaisuun ja ratkaista vakion
ensin.
- Piirrä kuva. Missä ratkaisu on määritelty?
(Newtonin jäähtymislaki)
- Eri ratkaisutapoja:
- Muuttujanvaihdolla
päästään yhtälöön
(esimerkki 1).
- Suoraan separointimenetelmällä:
- Muuttujanvaihdolla
- Eri ratkaisutapoja:
(Logistinen kasvu)
- Separointimenetelmällä; valitaan muuttujaksi nyt
(aika).
- Osamurtokehitelmä:
- Olettaen
saadaan
, josta
- Osamurtokehitelmä:
2.3 Sijoituksella separoituvaksi palautuva DY
- Joskus differentiaaliyhtälö voidaan palauttaa separoituvaksi muuttujanvaihdon avulla, esim.
sijoituksella
sijoituksella
- yhtälöitä
kutsutaan joskus tasa-asteisiksi, engl. homogeneous [A, s. 995]
- yhtälöitä
2.3.1 Esimerkki
Ratkaise alkuarvotehtävä
- Huomataan, että nolla ei voi kuulua ratkaisuvälille. Laajin mahdollinen ratkaisuväli on siis
.
- Muokataan ensin:
Tehdään muuttujanvaihto
eli
, jolloin
ja
- Ratkaistaan DY:
Sijoitetaan takaisin
ja rajoitetaan
, jolloin saadaan
- Alkuehdon
perusteella
, joten alkuehdon toteuttava ratkaisu on
2.4 Käyräparven DY ja kohtisuorat leikkaajat
2.4.1 Käyräparven DY
Differentiaaliyhtälön ratkaisun kuvaajaa kutsutaan usein integraalikäyräksi
- erityisesti silloin, kun yhtälöä ei voida ratkaista eksplisiittisesti, vrt. esimerkit 2 ja 3 edellä.
Vastaavasti vapaan vakion avulla annettua käyräparvea vastaa differentiaaliyhtälö, esim.
- origokeskiset ympyrät:
- kl:n DY:n normaalimuoto
antaa käyrän tangentin kulmakertoimen pisteessä
.
2.4.2 Kohtisuorat leikkaajat
Käyräparven kohtisuorilla leikkaajilla tarkoitetaan käyräparvea, jonka jokainen käyrä leikkaa alkuperäisen parven kutakin käyrää kohtisuorasti.
- Miten löydetään käyräparven kohtisuorat leikkaajat? Idea lyhyesti:
- käyräparven DY
- tangenttien kulmakertoimet
- (kohtisuoruusehto) uuden käyräparven tangenttien kulmakertoimet
- uuden käyräparven DY
- uusi käyräparvi
Esimerkki
- Etsi käyräparven
kohtisuorat leikkaajat.
- Ratkaisu yllä olevaa ideaa noudatellen:
- Derivoidaan käyräparven yhtälö, saadaan DY
Sijoitetaan alkuperäisestä yhtälöstä saatava
, jolloin
(Sama tulos saadaan myös toisella tavalla: ratkaistaan
käyräparven yhtälöstä ja derivoidaan vasta sitten.)
- Kohtisuorien leikkaajien DY on siis
- Ratkaistaan tämä DY, saadaan implisiittinen ratkaisu
ja edelleen
(ellipsiparvi).
- Derivoidaan käyräparven yhtälö, saadaan DY
3. Lineaarinen DY, osa I: yleistä sekä 1. kertaluvun lin. DY:n ratkaiseminen
- lineaarinen DY
- lineaarisen DY:n alkuarvotehtävän ratkaisun olemassaolo ja yksikäsitteisyys
- lineaarisen 1. kl:n DY:n ratkaiseminen, osa 1:
- homogeeninen separoimalla
- epähomogeeninen lisäämällä homogeenisen yleiseen ratkaisuun epähomogeenisen yksittäisratkaisu
- "arvataan" yksittäisratkaisu
3.0.1 Johdatteleva esimerkki
- Tiedetään (ks. 1. esimerkki kohdassa 2.2), että differentiaaliyhtälön
yleinen ratkaisu on
Miten löydettäisiin yhtälön
yleinen ratkaisu?
- Kokeilemalla löydetään yksittäisratkaisu
.
- Tarkista:
ja siksi
kaikilla
.
- Tarkista:
- Huomataan myös, että yhteenlaskulla saatava funktio
on yhtälön (2) ratkaisu jokaisella
.
- Tarkista:
ja siksi
kaikilla
.
- Tarkista:
- Siis yhtälön (2) yleinen ratkaisu on
- Yhtälön (2) yleinen ratkaisu saatiin siis lisäämällä
yhtälön (1) yleiseen ratkaisuun eräs yhtälön (2) yksittäisratkaisu.
- Kokeilemalla löydetään yksittäisratkaisu
- Huomioita/kysymyksiä, joita tässä luvussa käsitellään:
- Toimiiko johdatteluesimerkissä käytetty menetelmä yleisesti?
Millaisille differentiaaliyhtälöille? - Miten löydetään yksittäisratkaisu
?
(nopeammin kuin arvaa-kokeile-korjaa -menetelmällä)
- Toimiiko johdatteluesimerkissä käytetty menetelmä yleisesti?
3.1 Lineaarisen DY:n eri muodoista
Kuten kohdassa 1.5.1 määriteltiin, 1. kertaluvun lineaarinen DY on muotoa Jos kaikilla
on voimassa
, niin yhtälö voidaan kirjoittaa muodossa
eli
kun merkitään
ja
.
Tästä yhtälö voidaan saattaa normaalimuotoon
Huomautuksia
- Jos kerroinfunktiolla
on nollakohtia, yhtälöllä
voi olla ratkaisuja, jotka eivät ole normaalimuotoisen yhtälön ratkaisuja (eri määrittelyväli).
- Vrt. alkuarvotehtävän ratkaisujen olemassaolo- ja yksikäsitteisyys (1.4): lause koskee normaalimuotoista yhtälöä.
- (Kiinnostuneet löytävät varoittavan esimerkin P. Juutisen monisteesta luvun 2.2 lopusta.)
- Yleensä käsitellään varsinaisen normaalimuodon sijaan muotoa
- Tätä vastaavalla homogeenisella yhtälöllä (HY) tarkoitetaan yhtälöä
- Ratkeaa separoimalla (kuten yllä 3.0.1), tästä lisää myöhemmin.
- Kuten johdatteluesimerkissä 3.0.1 nähtiin, homogeenisen yhtälön ratkaiseminen on tärkeä osa epähomogeenisen yhtälön ratkaisua.
- Epähomogeenista yhtälöä voidaan kutsua myös täydelliseksi.
- Tätä vastaavalla homogeenisella yhtälöllä (HY) tarkoitetaan yhtälöä
3.2 Lineaarisen DY:n ominaisuuksia
Tarkastellaan lineaarista 1. kertaluvun epähomogeenista differentiaaliyhtälöä ja sitä vastaavaa homogeenista yhtälöä
Jatkossa oletetaan, että funktiot
ovat jatkuvia (jollain välillä
).
3.2.1 Ratkaisun olemassaolo ja yksikäsitteisyys
- Yhtälöllä (E1) on kullakin alkuehdolla yksikäsitteinen ratkaisu.
- Tämä seuraa lauseesta kohdassa 1.4, sillä
ja
ovat jatkuvia.
- Tämä seuraa lauseesta kohdassa 1.4, sillä
3.2.2 HY:n ratkaisujen lineaarikombinaatioista
- Jokainen homogeenisen yhtälön (H1) ratkaisuista muodostettu lineaarikombinaatio on myös yhtälön (H1) ratkaisu.
- Ks. huomiot alla.
Lause:
Jos
on homogeenisen yhtälön (H1) ratkaisu ja
on vakio, niin myös
on yhtälön (H1) ratkaisu.
Jos
ja
ovat homogeenisen yhtälön (H1) ratkaisuja, niin myös
on yhtälön (H1) ratkaisu.
- Todistus:
- Vakio säilyy derivoitaessa, joten
- Summa derivoidaan termeittäin, joten
- Vakio säilyy derivoitaessa, joten
Huomioita:
- Lauseen kaksi osaa voidaan kirjoittaa yhtenä:
josja
ovat HY:n ratkaisuja ja
ja
vakioita, niin myös
on HY:n ratkaisu.
- Vrt. [A, s. 992, Theorem 1]
- Pohdi: toimiiko epähomogeeniselle yhtälölle (E1)?
- Miksi ei? Millaisen yhtälön
toteuttaa, jos
ja
ovat yhtälön (E1) ratkaisuja?
- Miksi ei? Millaisen yhtälön
3.2.3 Epähomogeenisen DY:n muut ratkaisut
- Miten löydetään epähomogeenisen yhtälön (E1) muut ratkaisut yksittäisratkaisun ja HY:n yleisen ratkaisun avulla?
Lause [A, s. 992, Theorem 2]:
Jos on yhtälön (H1) yksittäisratkaisu ja
yhtälön (E1) yksittäisratkaisu, niin
on myös yhtälön (E1) yksittäisratkaisu.
- Todistus:
on yhtälön (E1) ratkaisu, koska
Lause:
Jos on yhtälön (H1) yksittäisratkaisu, joka ei ole nollafunktio, ja
on yhtälön (E1) yksittäisratkaisu, niin yhtälön (E1) yleinen ratkaisu on
ja näin saadaan kaikki ratkaisut.
- Todistuksen ideat:
- Edellisen lauseen nojalla jokainen
on yhtälön (E1) ratkaisu.
- Jos
ja
ovat yhtälön (E1) ratkaisuja,
niinon yhtälön (H1) ratkaisu:
- Pohdi: miksi tämä riittää?
- Edellisen lauseen nojalla jokainen
Huomioita
- Lauseen voisi kirjoittaa myös toisessa muodossa:
Joson yhtälön (H1) yleinen ratkaisu ja
yhtälön (E1) yksittäisratkaisu, niin yhtälön (E1) yleinen ratkaisu on
ja näin saadaan yhtälön (E1) kaikki ratkaisut.
- Tässä siis vapaa vakio
on piilossa (epämääräisen) ilmaisun "
on yleinen ratkaisu" takana.
- Vrt. johdatteleva esimerkki 3.0.1.
- Tässä siis vapaa vakio
3.3 Homogeenisen lin. 1. kl:n DY:n ratkaiseminen
Yhtälö (H1) eli voidaan kirjoittaa normaalimuotoon
ja separointimenetelmällä saadaan ratkaisuksi
missä
on jokin funktion
antiderivaatta.
- Tarkemmin: olkoon
jokin funktion
antiderivaatta.
- Vielä tarkemmin katsoen ensimmäinen
pitäisi perustella kohdan 1.4 avulla.
- Kiinnostuneet löytävät yksityiskohdat P. Juutisen monisteesta (s.8-9).
- Vielä tarkemmin katsoen ensimmäinen
Huomioita:
Ratkaisu ei riipu antiderivaatan valinnasta:
josja
ovat eri antiderivaatat, niin niiden erotus on vakio ja siksi
on vakio, joka sulautuu vapaaseen vakioon
.
Ratkaisu voidaan kirjoittaa myös "epämääräisemmilllä merkinnöillä"
3.4 Epähomogeenisen yhtälön yksittäisratkaisun löytämisestä (vakiokertoiminen yhtälö)
Tavoite: löytää jokin yhtälön (E1) eli toteuttava yksittäisratkaisu.
- Strategia, kun
on vakiofunktio:
- Arvataan ensin yksittäisratkaisun muoto funktion
perusteella ja käytetään vapaita kertoimia.
- Esimerkissä 3.0.1 ensimmäisen asteen polynomi:
- Tätä voidaan kutsua yritteeksi.
- Esimerkissä 3.0.1 ensimmäisen asteen polynomi:
- Selvitetään kertoimet, joilla yrite toteuttaa yhtälön (E1).
- Derivoidaan yrite ja sijoitetaan yhtälöön (E1).
- Yhtälön tulee toteutua kaikilla
; näin saadaan kerrointa (/kertoimia) koskeva(t) yhtälö(t).
- Arvataan ensin yksittäisratkaisun muoto funktion
- Vinkkejä yksittäisratkaisun muodon arvaamiseen, kun
(vakio):
| yrite | |
|---|---|
| polynomi | polynomi (samaa astetta) |
- Pohdi, miksi nämä ovat hyviä yritteitä, kun
on vakiofunktio.
- Miten täydentäisit taulukkoa?
Huomautus:
- Jos
ei ole vakiofunktio, hyvän yritteen keksiminen käy monimutkaiseksi.
- Tätä tilannetta käsitellään myöhemmin.
3.5 Esimerkkejä
- Ratkaise
- (Tämä ratkaistiin jo päättelemällä kohdassa 3.0.1.)
- Ratkaisu vaiheittain homogeenisen yhtälön yleisen ratkaisun ja polynomiyritteen avulla:
- Ratkaistaan ensin homogeeninen yhtälö
.
- (Jos merkinnät ovat selvät, alla olevista välivaiheista voi osan jättää poiskin.)
- Löydettiin homogeenisen yhtälön yleinen ratkaisu
.
- (Jos merkinnät ovat selvät, alla olevista välivaiheista voi osan jättää poiskin.)
- Etsitään sitten alkuperäisen, epähomogeenisen yhtälön yksittäisratkaisu.
- Käytetään yritettä
:
- Jotta alkuperäinen yhtälö toteutuu kaikilla
, on oltava
Tästä saadaan
ja
.
- Jotta alkuperäinen yhtälö toteutuu kaikilla
- Löydettiin yksittäisratkaisu
.
- Käytetään yritettä
- Yhdistetään tiedot:
- Yhtälön
yleinen ratkaisu on
- Yhtälön
- Ratkaistaan ensin homogeeninen yhtälö
- Ratkaise
.
- Ratkaisu vaiheittain:
- HY:
, tämän yleinen ratkaisu on
,
(laskettu yllä).
- Otetaan yritteeksi
.
- Yrite
toteuttaa yhtälön
, kun
Tästä saadaan
,
. Siis
on yhtälön
yksittäisratkaisu. (Tarkista itse.)
- Yrite
- Yhtälön
yleinen ratkaisu on
,
.
- HY:
- Ratkaise
.
- Ratkaisu vaiheittain:
- HY:
, tämän yleinen ratkaisu on
,
(laskettu yllä).
- Etsitään ensin yhtälön
toteuttava funktio
kuten esimerkissä 2:
- Otetaan yritteeksi
.
- Yrite
toteuttaa yhtälön
, kun
Tästä saadaan
,
. Siis
on yhtälön
yksittäisratkaisu. (Tarkista itse.)
- Otetaan yritteeksi
- Etsitään sitten yhtälön
toteuttava funktio
.
- Esimerkin 1 mukaan
kelpaa.
- Esimerkin 1 mukaan
- Yhtälön
yleinen ratkaisu on
- (Tarkista itse.)
- HY:
4. Lineaarinen DY, osa II: 1. kl. lin. jatkuu
- lineaarisen 1. kl:n DY:n ratkaiseminen, osa 2:
- epähomogeeninen lisäämällä homogeenisen yleiseen ratkaisuun epähomogeenisen yksittäisratkaisu
- etsitään yksittäisratkaisu vakion varioinnilla
- yleismenetelmä: etsitään integroiva tekijä
- epähomogeeninen lisäämällä homogeenisen yleiseen ratkaisuun epähomogeenisen yksittäisratkaisu
4.0.1 Johdattelua ja kertausta
- Aiemmin (ks. 3.2.3) todettiin, että lineaarisen 1. kertaluvun DY:n
yleinen ratkaisu saadaan vastaavan homogeenisen yhtälön
yleisen ratkaisun
ja yhtälön (E1) minkä tahansa yksittäisratkaisun
summana:
- Ideaa voi visualisoida tasossa origon kautta kulkevalla suoralla (yhtälön (H1) ratkaisut) ja sen kanssa yhdensuuntaisella suoralla (yhtälön (E1) ratkaisut).
- Jos kerroinfunktio
on vakio eli (E1) on vakiokertoiminen, niin joissakin tapauksissa yksittäisratkaisu on helppo "arvata":
- valitaan yritteen muoto funktion
perusteella
- sovitetaan kertoimet niin, että yrite toteuttaa yhtälön (E1).
- (ks. 3.4 ja 3.5)
- valitaan yritteen muoto funktion
- Entä, jos
- yritteen muodon päätteleminen suoraan funktion
perusteella menee vaikeaksi, tai
- kerroinfunktio
ei olekaan vakiofunktio?
- yritteen muodon päätteleminen suoraan funktion
4.1 Vakion variointi
Etsitään epähomogeenisen yhtälön (E1) yksittäisratkaisua yritteellä, jossa vastaavan homogeenisen yhtälön (H1) ratkaisussa esiintyvä vakio on korvattu funktiolla
.
4.1.1 Esimerkki
- Ratkaise vakion varioinnin avulla
, kun
.
- Kertaa homogeenisen yhtälön ratkaisu kohdasta 3.3.
- Ratkaisu:
- HY:
- HY:n yleinen ratkaisu on
,
- HY:n yleinen ratkaisu on
- Vakion variointi: etsitään sellainen funktio
, että
on yhtälön
ratkaisu. Derivoidaan:
Sijoitetaan yhtälön vasemmalle puolelle:
Jos
on yhtälön
ratkaisu, niin
ja siis
josta voidaan valita
- Nyt
on yhtälön
yksittäisratkaisu.
- Tarkista itse.
- Tarkista itse.
- Nyt
- Yhtälön
yleinen ratkaisu on
- Tarkista itse.
- HY:
- Huomautuksia:
- Keksitkö lisäksi jonkin toisen tavan, jolla yhtälö
osattaisiin ratkaista?
- Vakion variointia tarvitaan myös jatkossa.
- Keksitkö lisäksi jonkin toisen tavan, jolla yhtälö
4.2 Ratkaisu integroivan tekijän avulla
Ratkaistaan epähomogeeninen yhtälö (E1) kertomalla se ensin sopivalla lausekkeella niin, että saadun yhtälön
vasen puoli on tulon "jotakin kertaa y" derivaatta.
- Mieti:
- Sopiva funktio
olisi siis sellainen, että
.
- Valitaan
, missä
;
nyt, kuten haluttiin.
- Valitaan
- Sopiva funktio
- Saatu uusi DY voidaan ratkaista: ensin integroidaan ja sen jälkeen ratkaistaan
.
- Integroinnin jälkeen yhtälön vasemmalla puolella on tulo
eli
.
- Integroinnin jälkeen yhtälön vasemmalla puolella on tulo
Funktiota kutsutaan yhtälön
integroivaksi tekijäksi.
4.2.1 Esimerkki
- Ratkaise integroivan tekijän avulla
, kun
.
- Ratkaisu (kun
):
- Kerroinfunktiona
on
, joten integroiva tekijä on
(huom.
).
- Koska
, niin
- Kerroinfunktiona
- Saatiin sama ratkaisu kuin aiemmin vakion varioinnilla.
4.3 Lineaarisen 1. kl:n DY:n ratkaisukaava
Ratkaistaan yhtälö (E1) eli kahdella tavalla: 1) homogeenisen yhtälön ratkaisun ja vakion varioinnin sekä 2) integroivan tekijän avulla.
- Tapa 1:
- Ensin homogeeniyhtälön (H1) ratkaisu separointimenetelmällä (vrt. mm. esimerkki 1 kohdassa 3.5), saadaan
(integroimisvakio eksponentissa saadaan valita vaikkapa nollaksi).
- Sitten vakion variointi: tehdään yrite
, jolloin
ja sijoittamalla yrite yhtälön vasemmalle puolelle saadaan
Jotta tämä olisi yhtälön (E1) yksittäisratkaisu, täytyy olla
eli
Yhtälön (E1) yksittäisratkaisuksi löydetään
- Yhtälön (E1) yleinen ratkaisu on siis
eli (valitun) antiderivaatan
avulla kirjoitettuna
- Integraalimerkinnän vapaa integroimisvakio huomioiden tämä voidaan kirjoittaa myös muodossa
- Integraalimerkinnän vapaa integroimisvakio huomioiden tämä voidaan kirjoittaa myös muodossa
- Ensin homogeeniyhtälön (H1) ratkaisu separointimenetelmällä (vrt. mm. esimerkki 1 kohdassa 3.5), saadaan
- Tapa 2, integroivan tekijän avulla:
- Kerrotaan yhtälö (E1) integroivalla tekijällä
jolloin saadaan
- Jälleen käyttäen valitusta antiderivaatasta merkintää
saadaan muoto
- Jälleen käyttäen valitusta antiderivaatasta merkintää
- Kerrotaan yhtälö (E1) integroivalla tekijällä
4.3.1 Alkuarvotehtävä
Vastaavasti alkuarvotehtävän ratkaisu saadaan kaavalla
missä
- Tarkista itse.
5. Epälineaarinen 1. kl DY
- lisää separoituvasta DY:stä
- ratkaisukäyrien käyttäytyminen ja erikoisratkaisut
- integraaliyhtälö
- lineaariseksi palautuva DY
- Bernoullin yhtälö
- eksakti ja eksaktiksi palautuva DY
5.1 Separoituvasta DY:stä vielä
Tarkastellaan separoituvaa DY:ä Oletetaan, että
ja
ovat jatkuvia.
5.1.1 Kaikki ratkaisut?
- Jos funktiolla
ei ole nollakohtia, kaikki ratkaisut saadaan separoidun yhtälön
ratkaisuina.
- Jos funktiolla
on nollakohtia, niin em. ratkaisujen lisäksi yhtälöllä
on vakioratkaisuja:
- jos
on nolla, niin
on ratkaisu (tarkista itse).
- jos
- Jos
on jatkuvasti derivoituva, niin näiden lisäksi muita ratkaisuja ei ole.
- Alkuarvotehtävällä on yksikäsitteinen ratkaisu, koska
ja
ovat jatkuvia, ks. 1.4.
- Alkuarvotehtävällä on yksikäsitteinen ratkaisu, koska
5.1.2 Ratkaisukäyristä
Jos on jatkuvasti derivoituva, niin ratkaisukäyrät eivät leikkaa toisiaan.
- Jos jatkuvasti derivoituvalla funktiolla
on nollakohdat
, niin yhtälöllä
on erikoisratkaisut
, ja muiden ratkaisujen kuvaajat kulkevat suorien
välissä niitä sivuamatta.
- Esim. piirrä alla esimerkin 1 ratkaisukäyrät.
Sen sijaan
- esim. yhtälöllä
on ainakin kaksi alkuehdon
toteuttavaa ratkaisua,
ja
- Tarkista itse.
5.1.3 Muistutus lineaarisesta DY:stä
Yleinen lineaarinen 1. kl:n yhtälö on muotoa ja sitä vastava homogeeninen yhtälö
- Jälkimmäinen voidaan muokata separoituvan yhtälön muotoon:
- mutta alkuperäisellä yhtälöllä voi olla ratkaisuja myös väleillä, jotka sisältävät funktion
nollakohdan...
- mutta alkuperäisellä yhtälöllä voi olla ratkaisuja myös väleillä, jotka sisältävät funktion
- Välillä, jolla sekä
että
ovat jatkuvia ja
ei saa arvoa nolla, alkuarvotehtävällä on yksikäsitteinen ratkaisu.
5.1.4 Esimerkkejä
- Ratkaise
ja piirrä muutamia ratkaisukäyriä.
- Ratkaisu:
- Funktion
nollakohta on
, joten yhtälöllä on vakioratkaisu
.
- Lisäksi
- Näillä ratkaisuilla ei ole nollakohtia.
- Funktio
on jatkuvasti derivoituva, joten kaikki ratkaisut on löydetty:
tai
.
- Piirretään vielä kuvaajia.
- Huomataan, että mikään kuvaajista ei leikkaa x-akselia eli suoraa
.
- Huomataan, että mikään kuvaajista ei leikkaa x-akselia eli suoraa
- Funktion
- Ratkaise
ja piirrä ratkaisukäyriä. Miten vakioratkaisu
näkyy kuvassa?
- Kuten aiemmin, ratkaisuksi saadaan
,
.
- Kuvassa on piirretty ratkaisukäyrät vakion
arvoilla
.
- Ratkaisukäyrät eivät leikkaa toisiaan; erityisesti ne pysyvät suoran
ylä- tai alapuolella.
- Ratkaisukäyrät eivät leikkaa toisiaan; erityisesti ne pysyvät suoran
- Kuten aiemmin, ratkaisuksi saadaan
Tässä ei näy kuvaa.
AL: Mikä selain? (Minulla kyllä näkyy.)
Päivitys/tieto: ongelma ei johtunut selaimesta vaan kuvatiedoston lukuoikeuden puuttumisesta.
—- Ratkaise
alkuarvoilla
ja
.
- Mitä huomaat?
- Ratkaisu:
- Yhtälö on separoituva:
, missä
kaikilla
ja
, kun
.
- Siis yhtälöllä on erikoisratkaisu
. Funktio
on jatkuvasti derivoituva, joten muut ratkaisut eivät saa arvoa nolla missään.
- Siis yhtälöllä on erikoisratkaisu
- Etsitään yleinen ratkaisu separointimenetelmällä:
- Ratkaisuvälinä on joko
tai
(väli riippuu vakiosta
).
- Ratkaisuvälinä on joko
- Etsitään sitten alkuehdon
toteuttava ratkaisu:
, josta saadaan
.
- Siis alkuehdon
toteuttava ratkaisu on
,
.
- Siis alkuehdon
- Etsitään sitten alkuehdon
toteuttava ratkaisu:
, josta saadaan
.
- Siis alkuehdon
toteuttava ratkaisu on
,
.
- Siis alkuehdon
- Eri alkuehdoilla löydettiin siis eri väleillä määritelty ratkaisu.
- Ratkaisu ei pysy rajoitettuna, kun
lähestyy kohtaa
tai kohtaa
(ratkaisun nimittäjän nollakohtaa) - eikä tätä kohtaa nähdä suoraan yhtälöstä tai alkuehdosta...
- Ratkaisu ei pysy rajoitettuna, kun
- Yhtälö on separoituva:
- Ratkaise
ja piirrä yhtälön ratkaisukäyriä.
- Leikkaavatko ratkaisukäyrät toisiaan?
- Ratkaisu: yhtälö on separoituva, eikä funktiolla
ole nollakohtia.
- Tämä on implisiittinen ratkaisu, tyydytään siihen. Piirretään yhtälöä vastaavia tasokäyriä vakion
eri arvoilla.
- piirtovälineenä esim. GeoGebra, desmos.com tms.
- Käyrät eivät leikkaa toisiaan vakion eri arvoilla. Tämä nähdään myös siitä, että
on jatkuvasti derivoituva (määrittelyjoukossaan).
- Esim. alkuarvotehtävällä
on yksikäsitteinen ratkaisu, jonka implisiittinen muoto on
Derivoituvan funktion kuvaajalla ei ole pystysuoraa tangenttia; kuvan perusteella funktion määrittelyväliksi kelpaisi esim.
mutta ei esim.
.
- Toisaalta esim. alkuehdon
toteuttava ratkaisu on
ja kuvan perusteella ratkaisu on koko reaaliakselilla määritelty funktio.
- Muista myös yhtälön numeerinen ratkaiseminen, ks. Calculus 2, luku 6.
- Esim. alkuarvotehtävällä
- Kuvassa on ratkaisukäyriä vakion
arvoilla
.
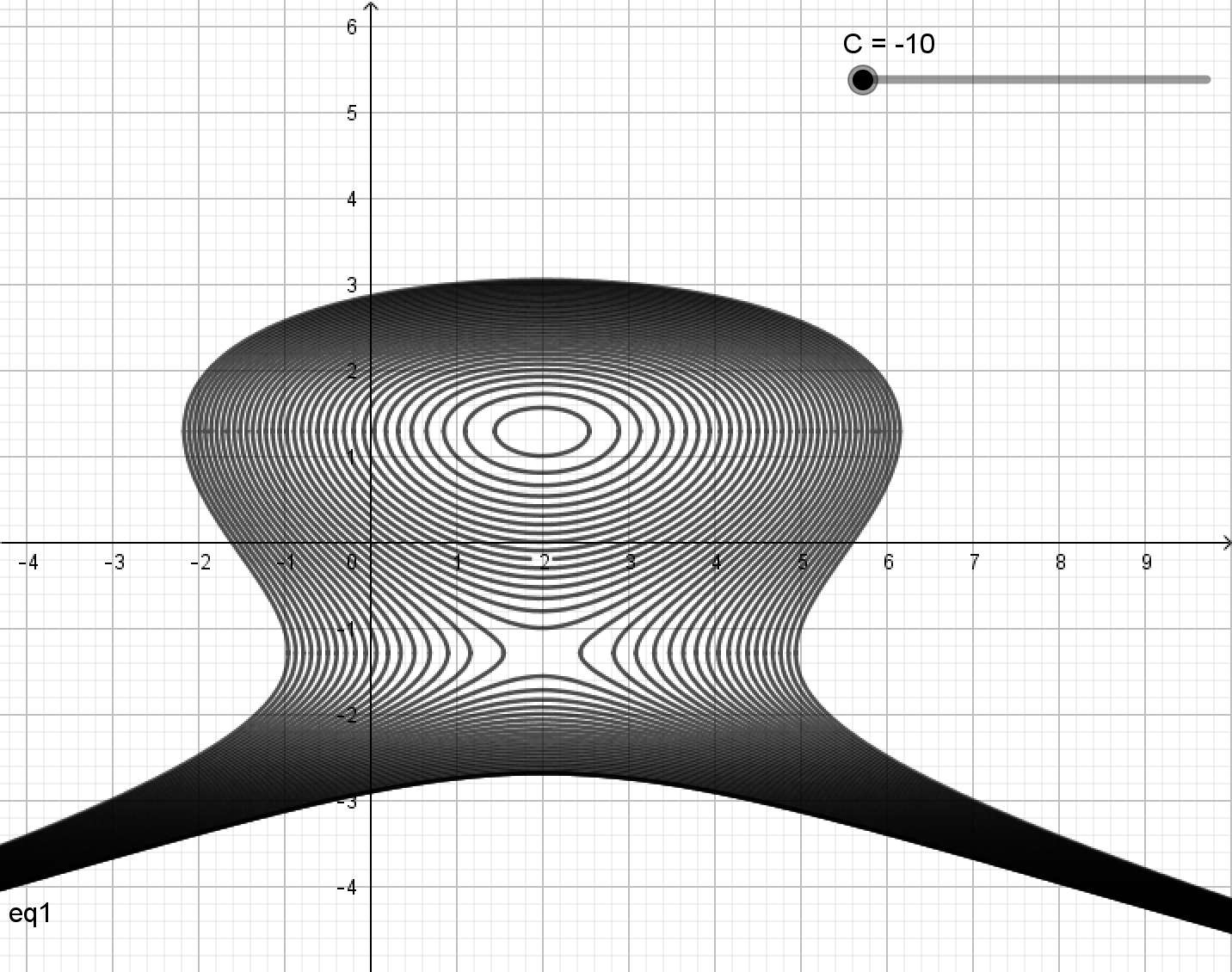
- Tämä on implisiittinen ratkaisu, tyydytään siihen. Piirretään yhtälöä vastaavia tasokäyriä vakion
5.2 Integraaliyhtälö
Jos derivaatan sijaan yhtälössä esiintyy tuntemattoman funktion (tai sen avulla muodostetun uuden funktion) integraalifunktio, voidaan differentiaaliyhtälön sijaan puhua integraaliyhtälöstä.
- Joskus integraaliyhtälöstä päästään differentiaaliyhtälöön derivoimalla yhtälö.
- Huom: yhtälön derivoinnissa katoaa tietoa:
,
mutta
jollakin
- Derivoinnissa "kadonnut" tieto vastaa differentiaaliyhtälön alkuehtoa.
- Huom: yhtälön derivoinnissa katoaa tietoa:
5.2.1 Esimerkki
- Ratkaise integraaliyhtälö
- Ratkaisu:
- Derivoidaan integraaliyhtälö muuttujan
suhteen, jolloin saadaan uusi yhtälö
- (Kertaa tarvittaessa analyysin peruslause, esim. Calculus 2, 11.2.1.)
- Tämä on separoituva yhtälö
, missä funktio
on jatkuvasti derivoituva ja sillä on yksi nollakohta, nolla.
- Niinpä yhtälöllä on vakioratkaisu
ja lisäksi separoimalla saatavat ratkaisut; kaikki voidaan esittää muodossa
- Niinpä yhtälöllä on vakioratkaisu
- Jotta alkuperäinen integraaliyhtälö
toteutuu, on oltava
.
- (Tämä nähdään siitä, että
.)
- (Tämä nähdään siitä, että
- Siis
ja integraaliyhtälön ratkaisu
- Derivoidaan integraaliyhtälö muuttujan
5.3 Lineaariseksi palautuva DY
Joskus epälineaarinen DY voidaan palauttaa lineaariseksi muuttujanvaihdolla.
- "Muuttujanvaihdolla" tarkoitetaan tässä, kuten aiemminkin, yhtälön kirjoittamista uuden funktion avulla.
5.3.1 Bernoullin yhtälöt
Yhtälöä kutsutaan Bernoullin yhtälöksi.
- Jos
tai
, yhtälö on lineaarinen (tarkista itse).
- Jos
ei ole
eikä 1, niin valitsemalla
yhtälö palautuu lineaariseksi:
ja saadaan
mikä on lineaarinen DY (tuntemattoman funktion
suhteen).
5.4 Eksakti DY
Tarkastellaan ensimmäisen kertaluvun DY:ä, joka on muotoa missä
ja
ovat kahden muuttujan funktioita.
Yhtälö voidaan kirjoittaa myös normaalimuodossa tai nk. differentiaalimuodossa
Jos funktioille ja
on voimassa
niin sanomme, että DY
on eksakti.
Jos yhtälö
on eksakti, niin on olemassa kahden muuttujan funktio
, jolle
ja yhtälön implisiittiseksi ratkaisuksi saadaan
,
.
Esimerkiksi yhtälön
eli
(implisiittinen) ratkaisu on
eli ratkaisukäyriä ovat kaikki origokeskiset ympyrät.
5.4.1 Esimerkki
- Totea, että yhtälö
on eksakti ja ratkaise se.
Hei, onko tuossa esimerkki 6:n yhtälön M(x,y)-osassa: 2x+sin(y-ye^-x), vai 2x+sin(y)-ye^-x?
AL: jälkimmäinen, \(\sin y = \sin (y)\)
—- Ratkaisu:
- Nyt
ja
- (Huomaa, että tässä
ja
ovat kahden muuttujan funktioita;
on "riippumaton muuttuja".)
- (Huomaa, että tässä
- Tarkistetaan, toteutuuko ehto
Vasen puoli:
Oikea puoli:
- Samat, joten yhtälö on eksakti.
- Etsitään funktio
, jolle
- Integroidaan
muuttujan
suhteen ja annetaan integroimisvakion riippua muuttujasta
:
- Valitaan
niin, että myös yhtälö
toteutuu:
Tämä on
, kun
eli kun
; valitaan vielä
.
- Löydettiin
- Integroidaan
- Yhtälön implisiittinen ratkaisu on
eli
- Nyt
5.4.2 Eksaktiksi palauttaminen integroivan tekijän avulla
Ensimmäisen kertaluvun DY ei välttämättä ole eksakti, vaikka se voitaisiinkin kirjoittaa muodossa Joskus ei-eksakti yhtälö voidaan muuttaa eksaktiksi kertomalla yhtälön kumpikin puoli samalla funktiolla, nk. integroivalla tekijällä. Erityisesti voidaan etsiä vain yhdestä muuttujasta riippuvaa integroivaa tekijää.
- Jos
jollakin
(eli ei riipu muuttujasta
lainkaan), niin yhtälölle
löytyy vain muuttujasta
riippuva integroiva tekijä
. Lisäksi integroiva tekijä
löydetään funktion
avulla:
- Tästä saadaan
.
- Tästä saadaan
- Mistä yllämainittu ehto on peräisin?
- Ehto saadaan yhtälön
eksaktisuusehdosta
ensin muotoon
ja siitä
jne.
- Ehto saadaan yhtälön
6. Ratkaisun olemassaolo ja yksikäsitteisyys sekä numeerisia ratkaisumenetelmiä
- Viivaelementtikenttä
- Ratkaisujen olemassaolo ja yksikäsitteisyys
- Alkuarvotehtävän ratkaiseminen numeerisesti
- Eulerin menetelmä
- parannettu Eulerin menetelmä
- Runge-Kutta -menetelmä
[A, 18.3]
6.0.1 Johdannoksi
Jos 1. kertaluvun differentiaaliyhtälöä ei osata ratkaista analyyttisin keinoin, mitä voidaan tehdä?
- Ratkaisukäyrien havainnollistaminen suoraan DY:stä
- viivaelementtikenttä
- Alkuarvotehtävän ratkaiseminen numeerisesti
- numeeriset menetelmät
Numeeristen ratkaisumenetelmien käyttäminen tarkoittaa approksimointia: lasketaan ratkaisufunktion arvojen likiarvoja numeerisesti. Tällöin on tärkeää tietää, että ratkaisu on olemassa.
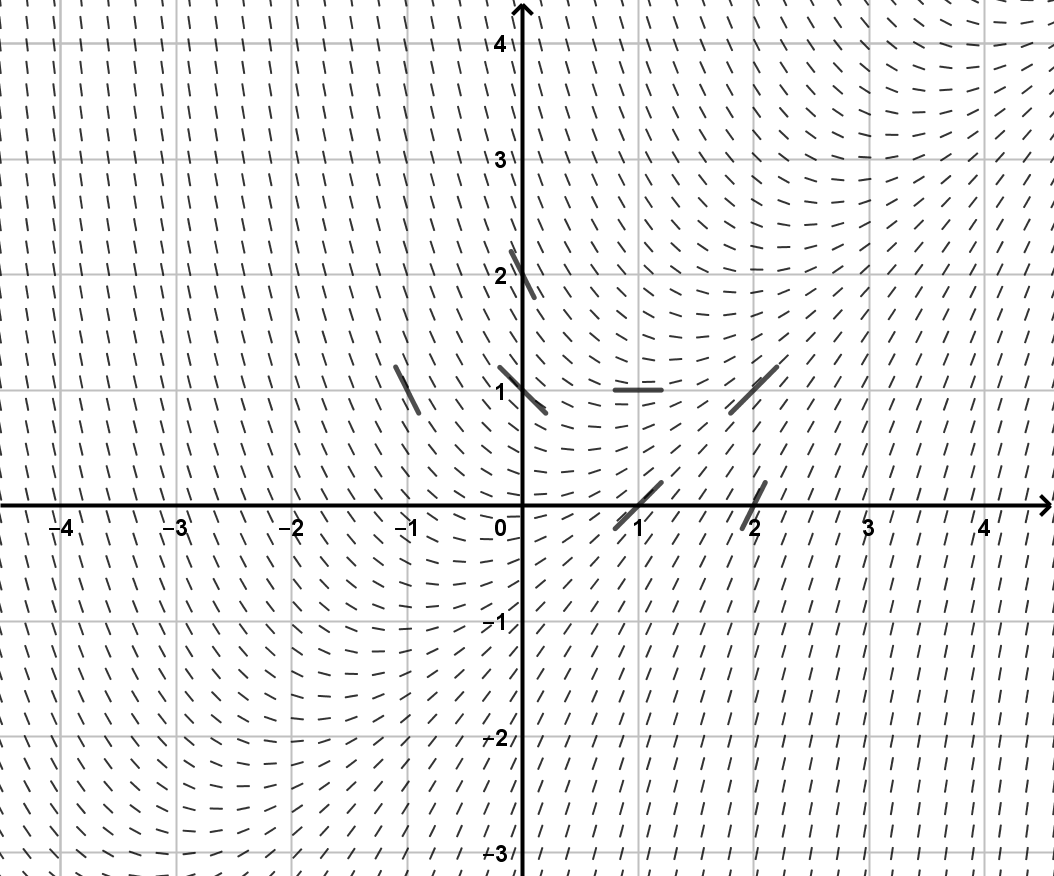
6.1 Viivaelementtikenttä
Jos toteuttaa normaalimuotoisen differentiaaliyhtälön
ja
eli piste
on funktion
kuvaajalla, niin kuvaajalle pisteeseen
piirretyn tangenttisuoran kulmakerroin on
Kuhunkin pisteeseen liittyy siis kulmakerroin
, jota voidaan havainnollistaa piirtämällä pisteeseen lyhyt jana tällä kulmakertoimella. Nämä jananpätkät muodostavat differentiaaliyhtälön
suunta- eli viivaelementtikentän (engl. slope field).
Esimerkiksi yhtälön viivakenttää voidaan hahmotella piirtämällä koordinaatistoon valittuihin pisteisiin
lyhyet jananpätkät, joiden kulmakertoimet saadaan lausekkeesta
:
| piste | kulmakerroin |
|---|---|
| (0,0) | 0 |
| (1,0) | 1 |
| (2,0) | 2 |
| (1,1) | 0 |
| (2,1) | 1 |
| (0,1) | -1 |
| (0,2) | -2 |
| (-1,1) | -2 |
| (jne.) |
Hei, kuvat eivät näyttäisi toimivan luentorungossa.
AL: Onpas merkillistä. Minulla näkyy kaikilla selaimilla ja kaikilla koneilla… Selvitellään asiaa.
Lisäys: Tämä ongelma selvisi pian, liittyi kuvatiedostojen lukuoikeuksiin.
—Kun pisteitä valitaan enemmän (ja viivat piirretään lyhyemmiksi), viivaelementtikenttä havainnollistaa yhä paremmin ratkaisukäyriä:
Yhtälö osataan ratkaista; kyse on lineaarisesta epähomogeenisestä vakiokertoimisesta differentiaaliyhtälöstä
jonka yleinen ratkaisu on
Piirretään alkuehtoja ,
,
ja
vastaavat ratkaisukäyrät samaan kuvaan viivaelementtikentän kanssa:
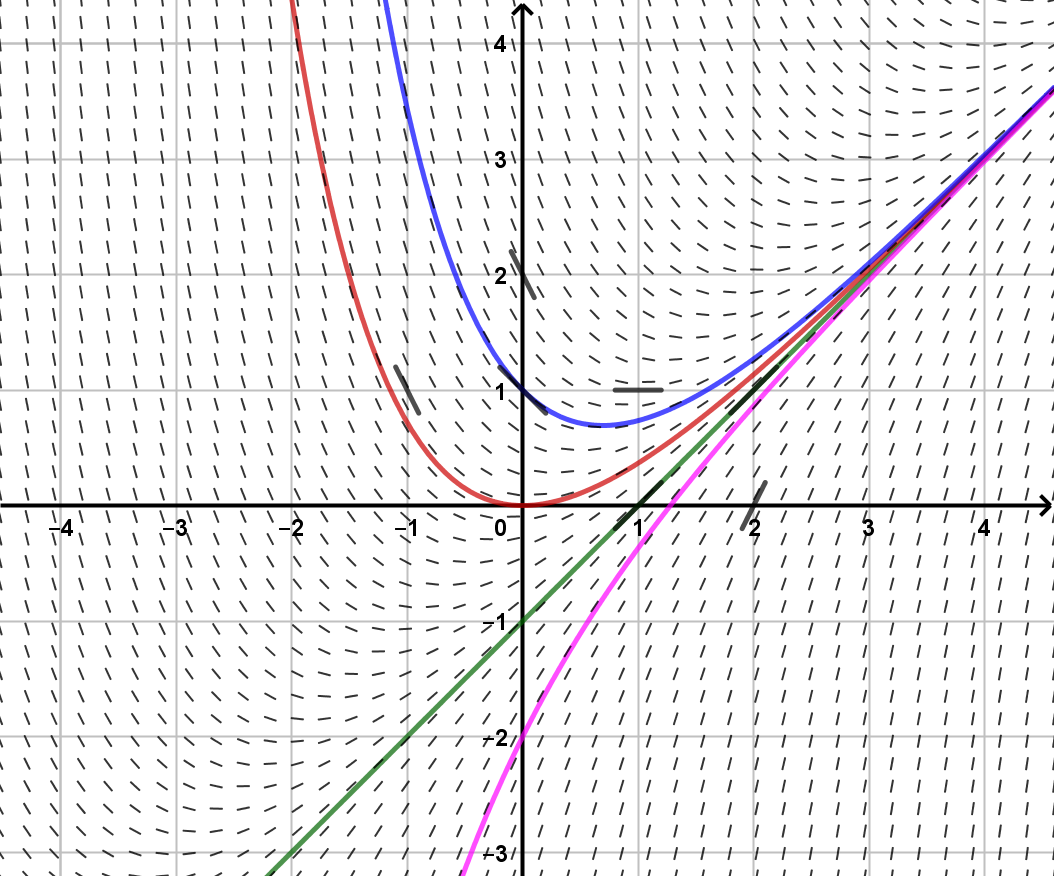
Huomataan, miten ratkaisukäyrät noudattelevat viivaelementtikentän viivoja - tai kääntäen, miten ratkaisukäyriä voitaisiin hahmotella viivaelementtikentän perusteella ratkaisematta yhtälöä.
Tämä yhtälön ratkaisukäyrien hahmottelu viivaelementtikentän perusteella onnistuu myös siinä tapauksessa, että yhtälöä
ei osata ratkaista.
6.2 Ratkaisun olemassaolo ja yksikäsitteisyys
Kohdassa 1.4 nähty alkuarvotehtävän ratkaisun yksikäsitteisyys- ja olemassaololause on tärkeä myös - ja erityisesti! - silloin, kun differentiaaliyhtälöä ei osata analyyttisin keinoin ratkaista. Alla vielä sama lause uudelleen:
Oletetaan, että funktiot ja
ovat jatkuvia suorakulmioalueessa, jossa
ja
, ja että piste
on suorakulmion sisällä.
Tällöin löytyy ja yksikäsitteinen välillä
määritelty derivoituva funktio
, jolle
ja
kaikilla
.
Ts. alkuarvotehtävällä on yksikäsitteinen ratkaisu välillä
.
[A, s. 1000 tai B, s. 24]
Huomautuksia (toisto)
- Lause siis sanoo kaksi asiaa:
- alkuarvotehtävällä on ratkaisu ("ratkaisun olemassaolo")
- ratkaisuja on vain yksi ("ratkaisun yksikäsitteisyys")
- Lauseesta seuraa mm. se, että lauseen oletukset täyttävällä differentiaaliyhtälöllä
ratkaisujen kuvaajat eivät leikkaa.
6.2.1 Todistuksen idea
Lauseen alkuarvotehtävä voidaan esittää yhtäpitävästi integaaliyhtälön muodossa:
on alkuarvotehtävän
ratkaisu, jos ja vain jos
Rakennetaan jono funktioita, jotka lähenevät ratkaisua :
Näitä kutsutaan Picardin iteraatioiksi. Ratkaisun olemassaolon todistus saadaan, kun osoitetaan, että rajafunktio on olemassa ja toteuttaa yllä olevan integraaliyhtälön.
- Tämä vaatii tietoja funktiojonon suppenemisesta; aihetta käsitellään ainakin kurssilla JMA4.
- Kiinnostuneet löytävät todistuksen esim. Petri Juutisen luentomonisteesta.
Ratkaisun yksikäsitteisyyden todistuksessa voidaan käyttää Gronwallin lemmaa: jos on jatkuvasti derivoituva välillä
,
ja
, niin
- Lemman avulla kahden alkuarvotehtävän ratkaisun erotus osoitetaan nollaksi koko tutkittavalla välillä; todistusta ei käsitellä tämän enempää tällä kurssilla.
- Kiinnostuneet löytävät todistuksen esim. Petri Juutisen luentomonisteesta.
6.2.2 Esimerkkejä ja huomautuksia
- Alkuarvotehtävä, jolla on useita ratkaisuja:
- Ratkaisuja ainakin kaksi:
ja
.
- (Tästä puhuttiin jo aiemmin kohdassa 5.1.2.)
- Huomaa, että tässä
on jatkuva kaikkalla (eli koko
-tasossa),
- mutta
ei ole edes määritelty
akselilla eli kun
;
- siis
ei ole jatkuva missään origon eli pisteen
sisältävässä suorakulmioalueessa
- eli lauseen oletus ei ole voimassa.
- Ratkaisuja ainakin kaksi:
- Alkuarvotehtävän ratkaisu ei välttämättä ole määritelty koko välillä
(tai koko reaaliakselilla, vaikka lauseen oletus olisi voimassa koko
-tasossa); ks. esimerkki 3 kohdassa 5.1.4.
6.3 Numeerisia ratkaisumenetelmiä
Tarkastellaan alkuarvotehtävää ja oletetaan, että olemassaolo- ja yksikäsitteisyyslauseen oletukset täyttyvät eli että tehtävällä on yksikäsitteinen ratkaisu
jollakin kohdan
sisältävällä välillä.
Vaikka DY:ä ei osattaisi ratkaista eksplisiittisesti eli funktiolle ei löydettäisi lauseketta muuttujan
avulla, sen arvoja voidaan approksimoida halutuissa kohdissa. Tarkastellaan kolmea approksimointimenetelmää.
Ideana on laskea approksimaatio funktion arvolle kohdassa eli arvolle
käyttäen
askelta. Samalla tullaan laskeneeksi approksimaatiot myös funktion arvoille kohdissa
.
Merkintöjä
askeleen pituus oikealle edettäessä
- jos
, menetelmä etenee vasemmalle
- jos
,
menetelmän antama approksimaatio arvolle
6.3.1 Eulerin menetelmä
Murtoviiva-approksimaatio, jossa kunkin osan kulmakerroin on laskettuna osan alkupisteessä (ja vaaka-suuntainen etenemä
, koska
).
- Iteraatiokaava:
Esimerkki:
- Lasketaan kohdassa 6.1 käsitellyn alkuarvotehtävän
Eulerin menetelmän approksimaatiot välillä
käyttäen
- askelpituutta
ja viittä askelta
- askelpituutta
ja 10 askelta.
Verrataan lisäksi tuloksia tunnettuun ratkaisuun. Mikä on menetelmän virhe?
- askelpituutta
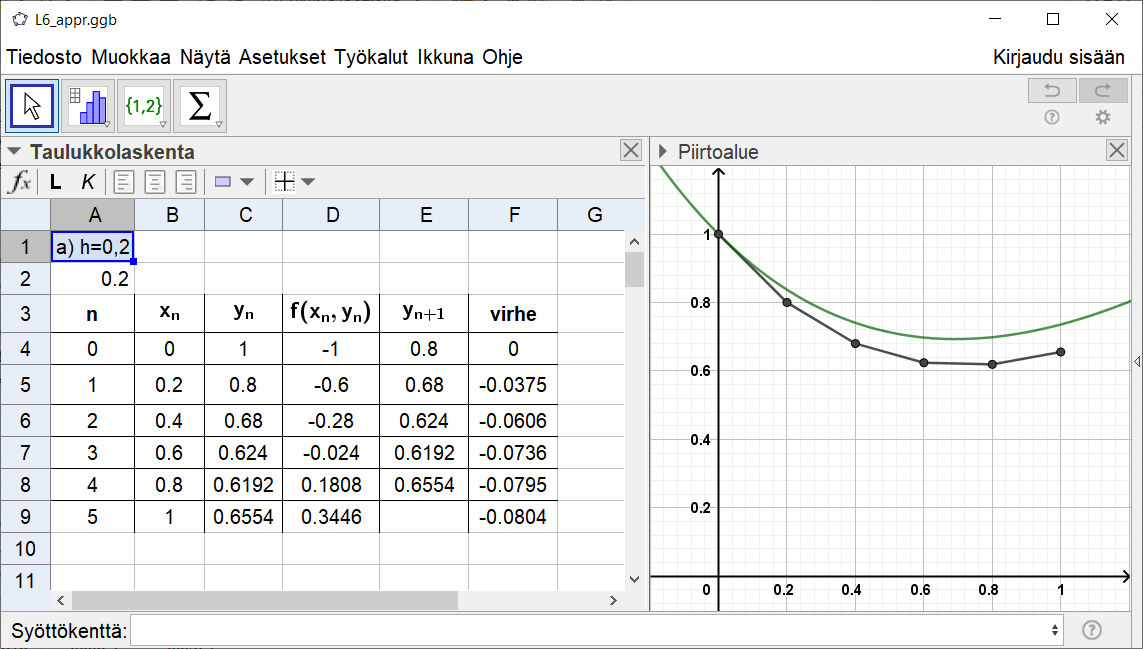
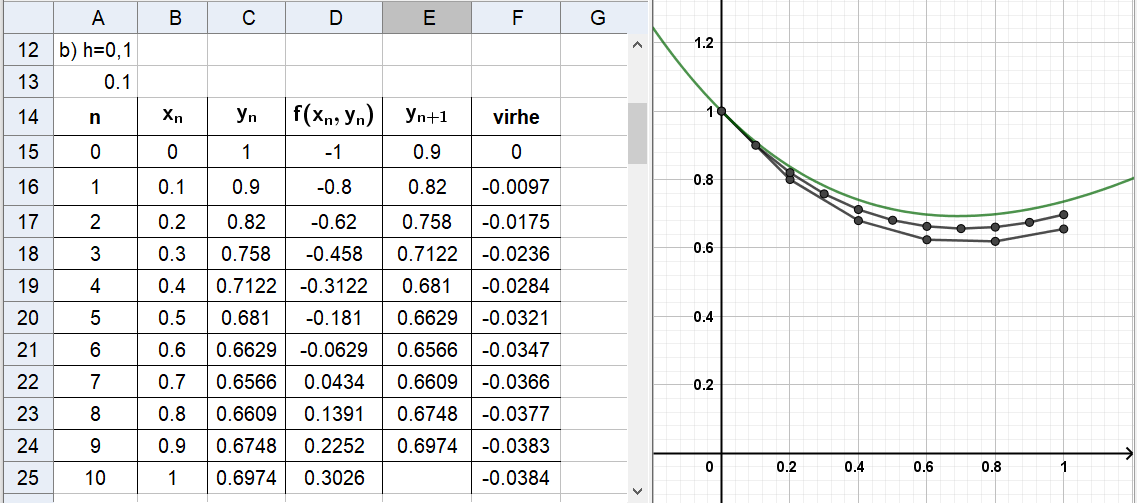
- Huomataan:
- ensimmäisen askeleen jälkeen virhe on b-kohdassa noin neljäsosa a-kohdan virheestä,
- välin päätepisteessä (
) b-kohdan virhe on noin puolet a-kohdan virheestä.
Eulerin menetelmässä
- yhden askeleen virhe on verrannollinen askeleen pituuden neliöön
- kumuloitunut virhe kohdassa
on verrannollinen lukuun
- Esim. jos halutaan pienentää virhe kymmenesosaan, on laskentapisteiden määrä
kymmenkertaistettava.
- Esim. jos halutaan pienentää virhe kymmenesosaan, on laskentapisteiden määrä
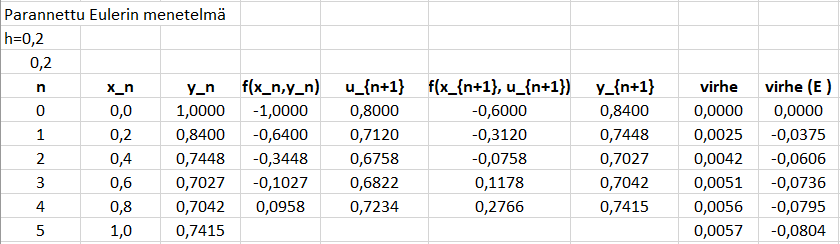
6.3.2 Parannettu Eulerin menetelmä
Murtoviiva-approksimaatio, jossa kunkin osan kulmakertoimeksi lasketaan funktion arvojen keskiarvo "päätepisteissä"; tuntematon päätepiste lasketaan Eulerin menetelmällä.
- Iteraatiokaava:
Esimerkki:
- Lasketaan kohdassa 6.1 käsitellyn alkuarvotehtävän
parannetun Eulerin menetelmän approksimaatiot välillä
käyttäen askelpituutta
ja viittä askelta.
- Verrataan lisäksi tuloksia Eulerin menetelmän tuloksiin.
Parannetussa Eulerin menetelmässä
- kussakin kohdassa lasketaan funktion arvo kahdesti
- eli laskentavaativuus on Eulerin menetelmään nähden kaksinkertainen
- kun
on riittävän siisti,
- approksimaatiovirhe on (korkeintaan) verrannollinen lukuun
- kumuloituva virhe kohdassa
on (korkeintaan) verrannollinen lukuun
- eli kymmenkertaistamalla
pienenee virhe sadasosaan.
- eli kymmenkertaistamalla
- approksimaatiovirhe on (korkeintaan) verrannollinen lukuun
6.3.3 Runge-Kutta -menetelmä
Neljännen kertaluvun Runge-Kutta -menetelmässä murtoviivan osien kulmakertoimet lasketaan käyttäen funktion arvoja tietyissä, erikseen laskettavissa pisteissä.
Iteraatiokaava:
missä
Menetelmän virhe on noin
parannetun Eulerin menetelmän virheestä esimerkin tapauksessa (ks. [A, s. 1005]).
Funktion
arvoja lasketaan kaksinkertainen määrä (ja nelinkertainen Eulerin menetelmään verrattuna).
Kumulativinen virhe on verrannollinen askelpituuden neljänteen potenssiin
, josta nimi.
7. Lineaarinen DY, osa III: 2. kl. lin. vakiokertoiminen DY (osa 1: homogeeninen)
- Yleistä 2. kl:n DY:istä
- Eräitä erikoistapauksia
- Alkuarvotehtävästä
- Lineaarisen 2. kl:n DY:n ominaisuuksia
- HY:n ratkaisujen lin. riippumattomuus, ratkaisukanta, kaikki ratkaisut
- Vakiokertoimisen HY:n ratkaiseminen
- Karakteristinen yhtälö ja sen käyttö
[A, 18.4 ja 3.7] sekä osin [B, 3.1-3.5]
7.0.1 Johdattelevia havaintoja
Havaintoja eksponenttifunktiosta:
- Jos
, niin
eli
toteuttaa DY:t
,
,
jne.
- Jos
, niin
eli
toteuttaa DY:t
ja
- Jos
, niin
eli
toteuttaa DY:t
ja
- Jos
- Havaintoja sini- ja kosinifunktiosta:
- Jos
, niin
eli
toteuttaa DY:n
.
- Jos
, niin
eli
toteuttaa DY:n
.
- Tee itse vastaavat havainnot kosinifunktiosta.
- Jos
- Yhteenvetoa havainnoista:
- Yhtälölle
löydettiin ainakin yksittäisratkaisut
ja
.
- Näitä ei saada toisistaan vakiolla kertomalla!
- Näitä ei saada toisistaan vakiolla kertomalla!
- "Lähes samannäköisille" yhtälöille
löydettiin kokeilemalla "aivan eri näköisiä" yksittäisratkaisuja;
- ensimmäiselle eksponenttifunktion,
- jälkimmäiselle trigonometristen funktioiden avulla.
- Yhtälölle
7.0.2 Johdatteleva esimerkki
Tehtävä:
- Etsi yhtälölle
kaksi ratkaisua
ja
,
- joita ei saada toisistaan vakiolla kertomalla
(eli joille ei millään vakiollapäde
kaikilla
).
- joita ei saada toisistaan vakiolla kertomalla
Ratkaisu:
- Arvataan, että ratkaisuksi voisi sopia
jollakin vakiolla
.
- Jos
, niin
joten
- Tämä on nolla täsmälleen silloin, kun
eli kun
tai
(mieti, miksi).
- Tämä on nolla täsmälleen silloin, kun
- Arvaus tuotti siis funktiot
ja
.
- Totea itse, että kumpikin toteuttaa alkuperäisen DY:n.
- Totea itse, että kumpikin toteuttaa alkuperäisen DY:n.
- Jos
- Löydettiin DY:n ratkaisut polynomiyhtälön
avulla.
- Tämä toimii - ainakin, kun polynomiyhtälöllä on kaksi eri (reaalista) ratkaisua.
- Tästä lisää tänään.
7.1 Toisen kertaluvun DY, yleistä
Toisen kertaluvun DY voidaan aina kirjoittaa implisiittimuodossa ja joskus lisäksi normaalimuodossa
(Käsitteistä puhuttiin jo kohdassa 1.1.)
7.1.1 Yksinkertaistuvia erikoistapauksia
Joskus toisen kertaluvun DY voidaan ratkaista aiemmin opituilla keinoilla kuten integroimalla tai palauttamalla se 1. kl:n DY:ksi.
- Yhtälö
ratkeaa integroimalla kahdesti.
- Yhtälössä ei esiinny
eikä
.
- Yhtälössä ei esiinny
- Yhtälö
palautuu 1. kl:n yhtälöksi merkinnällä
.
- Yhtälössä ei esiinny
.
- Yhtälössä ei esiinny
- Yhtälö
palautuu 1. kl:n yhtälöksi kertomalla derivaatalla
ja integroimalla, jolloin saadaan
- Yhtälössä ei (alunperin) esiinny
eikä
.
- Yhtälössä ei (alunperin) esiinny
- Yhtälö
palautuu 1. kl:n yhtälöksi tempulla, jossa
otetaan uudeksi muuttujaksi, josta uusi tuntematon funktio
riippuu:
Tällöin
ja yhtälöksi saadaan
- [A, s. 1008]
- Yhtälössä ei alunperin esiinny
.
7.1.2 Alkuarvotehtävä
- Toisen kertaluvun DY:n yleisessä ratkaisussa esiintyy yleensä kaksi toisistaan riippumatonta vakiota.
- Vrt. integrointi kahdesti.
- Vakioiden arvojen kiinnittämiseksi ei riitä funktion arvo yhdessä kohdassa; tarvitaan kaksi ehtoa.
- Alkuarvotehtävässä kiinnitetään yleensä sekä funktion arvo että sen derivaatan arvo tietyssä kohdassa.
- Alkuehdot annetaan samassa kohdassa; "alkuhetkellä".
- Jos derivaatan arvon sijaan kiinnitetäänkin itse funktion arvo alkuhetken lisäksi myös toisessa kohdassa, puhutaan alkuarvotehtävän sijaan reuna-arvotehtävästä.
- Normaalimuotoisen yhtälön alkuarvotehtävälle on vastaavanlainen ratkaisujen yksikäsitteisyys- ja olemassaololause kuin 1. kertaluvun yhtälöille.
- Tarkemmin: [B, 3.1]
7.1.3 Esimerkkejä
- Ratkaise alkuarvotehtävä
- (Huomataan, että yhtälössä ei esiinny
lainkaan.)
- Merkitsemällä
saadaan
Derivaattaa koskevasta alkuehdosta
saadaan
eli, josta edelleen
. Siis
- Palataan alkuperäiseen merkintään:
Tästä saadaan integroimalla
Alkuehdosta
saadaan
, joten alkuehdon toteuttava ratkaisu on
- Ratkaise
.
(Huomataan, että yhtälössä ei esiinny muuttuja
yksin lainkaan; yhtälö on muotoa
. Käytetään yllä mainittua temppua.)
Merkitään
, jolloin
eli
ja yhtälöksi saadaan
(muuttujana
, tuntemattomana funktiona
).
- Separoimalla saadaan (nollaratkaisun lisäksi)
josta integroimalla
:n suhteen
ja yleiseksi ratkaisuksi
.
- Separoimalla saadaan (nollaratkaisun lisäksi)
Palataan alkuperäiseen merkintään:
Nollaratkaisun lisäksi saadaan separoimalla ja integroimalla muuttujan
suhteen
eli yleinen ratkaisu on
Tarkista itse.
7.2 Lineaarinen 2. kl:n DY, yleistä ja ominaisuuksia
Edellä mainittujen yksinkertaistuvien erikoistapausten lisäksi tällä kurssilla käsittelemme 2. kl:n DY:istä lähinnä vain lineaarisia.
Kuten kohdassa 1.5.1 määriteltiin, sanomme 2. kl:n DY:ä lineaariseksi, jos se on muotoa missä oletamme, että kerroinfunktiot
ja
ovat jatkuvia (jollakin välillä
).
- Jos
on nollafunktio, yhtälöä (L2) sanotaan homogeeniseksi (HY), muutoin epähomogeeniseksi.
- Jos kerroinfunktiot
ja
ovat vakiofunktioita, yhtälöä (L2) kutsutaan vakiokertoimiseksi.
- Huomaa, että funktion
eli "epähomogeenisen osan" ei tarvitse olla vakiofunktio.
- Huomaa, että funktion
- Jos kerroinfunktiot ovat jatkuvia, normaalimuotoisen lineaarisen DY:n
alkuarvotehtävällä on yksikäsitteinen ratkaisu.
- Alkuehdot määräävät sekä funktion arvon että derivaatan arvon; siis sekä pisteen kuvaajalta että kuvaajan tangentin kulmakertoimen tässä pisteessä.
- Kuten 1. kl:n tapauksessa, kohdissa, joissa
, voi yhtälön (L2) ratkaisu käyttäytyä eri tavalla kuin yhtälön
ratkaisu.
Lause:
Jos ja
ovat lineaarisen homogeenisen yhtälön ratkaisuja ja
ovat vakioita, niin myös
on yhtälön ratkaisu.
- Todistetaan vastaavasti kuin 1. kl:n tapauksessa
- tai kuten yleisesti (kertalukuna
): ks. [A, s. 992, Theorem 1].
- tai kuten yleisesti (kertalukuna
Kysymys:
- Milloin näin saadaan kaikki ratkaisut?
- Idea: kun ratkaisut
ja
ovat riittävän erilaisia niin, että summa
ei sievene muotoon
tai
.
- Idea: kun ratkaisut
Määritelmä:
Sanomme, että funktiot ja
ovat lineaarisesti riippumattomia (LI), jos yhtälö
toteutuu vain, kun
,
ts. ei löydy vakiota , jolle olisi
kaikilla
.
Lause:
Jos ja
ovat lineaarisen homogeenisen yhtälön
lineaarisesti riippumattomia ratkaisuja,
niin yhtälön (H2) yleinen ratkaisu on ja näin saadaan kaikki ratkaisut.
- Tällöin sanomme, että funktiot
ja
muodostavat yhtälön (H2) ratkaisukannan.
- Todistus jätetään aiheesta syvällisemmin kiinnostuneille, esim. P. Juutisen moniste, s. 31-33 sekä [B, 3.2].
7.3 Vakiokertoimisen HY:n ratkaiseminen karakteristisen yhtälön avulla
Tarkastellaan seuraavaksi lineaarista 2. kertaluvun homogeenista vakiokertoimista yhtälöä
- Johdattelevassa esimerkissä 7.0.2. löydettiin yhtälölle
kaksi ratkaisua,
ja
, polynomiyhtälön
ratkaisujen
ja
avulla.
- Nyt tiedetään lisäksi, että yhtälön yleinen ratkaisu on
sillä
ja
ovat lineaarisesti riippumattomat.
- Nyt tiedetään lisäksi, että yhtälön yleinen ratkaisu on
7.3.1 Karakteristinen yhtälö
Lineaarisen, homogeenisen, vakiokertoimisen 2. kertaluvun DY:n karakteristinen yhtälö on
ja differentiaaliyhtälön (*) ratkaisut löytyvät yhtälön (**) ratkaisujen
ja
avulla.
- Tiedetään, että toisen asteen polynomiyhtälöllä on joko
- kaksi erisuurta reaalista ratkaisua,
- yksi kaksinkertainen reaalinen ratkaisu tai
- ei yhtään reaalista ratkaisua; tällöin yhtälöllä on kuitenkin
- kaksi kompleksista ratkaisua, jotka ovat toistensa konjugaatit.
- Yhtälön (**) ratkaisut saadaan toisen asteen yhtälön ratkaisukaavalla
kun tilanteessa
käytetään merkintää
, missä
on imaginaariyksikkö.
- Kertaa tarvittaessa esim. Calculus 1, luku 4.4 kompleksiluvuista.
7.3.2 Kaksi reaalijuurta
Jos yhtälöllä (**) on reaaliset ratkaisut ja
,
, niin
ja
muodostavat DY:n (*) ratkaisukannan ja
- DY:n (*) yleinen ratkaisu on
- Tämä voidaan perustella vastaavasti kuin johdatteluesimerkissä 7.0.2 ja kohdan 7.3 alussa yllä tehtiin.
7.3.3 Yksi (kaksinkertainen) juuri
Jos yhtälöllä (**) on vain yksi reaalinen ratkaisu , niin
ja
muodostavat DY:n (*) ratkaisukannan ja
- DY:n (*) yleinen ratkaisu on
- Perusteluksi riittää huomata, että
ja
ovat lineaarisesti riippumattomat ja todeta laskemalla, että
toteuttaa DY:n (*).
7.3.4 Kompleksiset juuret
Jos yhtälöllä (**) on ratkaisut ja
, niin
ja
muodostavat DY:n (*) ratkaisukannan ja
- DY:n (*) yleinen ratkaisu on
Onko tuohon jokin erityinen syy, että miksi kompleksisten juurten yhteydessä r-muuttujalla ei ole alaindeksiä toisin kuin reaalijuurten tapauksissa?
—Ei ole tarvetta merkitä erikseen, kun käytetään “lausekkeita” \(k+i\omega\) ja \(k-i\omega\). Alaindeksi on tarpeen edellisissä kohdissa, kun halutaan viitata eri ratkaisuihin, eikä niille ole muuta merkintää.
—- Tämän perusteluksi riittää, kuten edellä, havaita funktioiden
ja
lineaarinen riippumattomuus sekä todeta laskemalla, että
on ratkaisu kaikilla
.
- (Mutta mistä ratkaisun muodon voi keksiä / muistaa?)
- (Mutta mistä ratkaisun muodon voi keksiä / muistaa?)
- (+) Toisaalta perustelussa voidaan käyttää tietoja kompleksisesta eksponenttifunktiosta:
, kun
, joten kompleksiarvoisista funktioista
(vrt. reaalijuurten antamat
ja
)
saadaan sopivina lineaarikombinaatioina reaaliarvoiset funktiotja
missä käytettiin myös tietoja sinin parittomuudesta ja kosinin parillisuudesta.
7.3.5 Esimerkkejä
- Ratkaise
.
- DY on lineaarinen, homogeeninen, vakiokertoiminen 2. kertaluvun DY, joten se ratkeaa karakteristisen yhtälön avulla.
- DY:n karakteristinen yhtälö on
- Karakteristisella yhtälöllä on kaksi reaalista ratkaisua:
ja
.
- Niinpä DY:n yleinen ratkaisu on
- DY:n karakteristinen yhtälö on
- Ratkaise
.
- Karakteristinen yhtälö on
ja sen ainoa ratkaisu on
.
- Tämän perusteella DY:n yleinen ratkaisu on
- Ratkaise
.
- Karakteristinen yhtälö on
- Tämän yhtälön ratkaisut ovat
- DY:n yleiseksi ratkaisuksi saadaan näiden avulla
- Tämän yhtälön ratkaisut ovat
- Ratkaise alkuarvotehtävä
,
,
.
- DY:n
karakteristinen yhtälö on
jonka ratkaisut ovat
- DY:n yleinen ratkaisu on
- Alkuehdosta
saadaan
ja
derivaattaakoskevasta alkuehdosta
saadaan
, josta
.
- Siis alkuehdon toteuttava ratkaisu on
8. Lineaarinen DY, osa IV: 2. kl. lin. vakiokertoiminen DY (osa 2: epähomogeeninen)
- Lineaarisen epähomogeenisen DY:n yleinen ratkaisu
- HY:n yleisen ratkaisun ja epähomogeenisen yhtälön yksittäisratkaisun avulla
- Yksittäisratkaisun etsiminen
- vakiokertoimiselle yhtälölle joskus valistuneesti arvatun yritteen avulla
- (yleisesti vakion varioinnilla; siitä myöhemmin)
- Sovelluksista hiukan
- harmoninen värähtelijä
8.1 Lineaarisen 2. kl:n DY:n ominaisuuksia (jatkoa)
- Lineaarisen 2. kertaluvun differentiaaliyhtälön ominaisuuksia käsiteltiin jo aiemmin kohdassa 7.2;
- ks. erityisesti HY:n yleinen ratkaisu kahden lineaarisesti riippumattoman yksittäisratkaisun avulla.
Tarkastellaan nyt lineaarista 2. kertaluvun epähomogeenista differentiaaliyhtälöä ja sitä vastaavaa homogeenista yhtälöä
Oletetaan edelleen, että funktiot
ovat jatkuvia (jollain välillä
).
Kuten 1. kl:n tapauksessa, myös korkeampien kertalukujen lineaarisen epähomogeenisen DY:n ratkaisuun voidaan lisätä vastaavan homogeenisen yhtälön ratkaisu, ja summa on edelleen epähomogeenisen yhtälön ratkaisu (ks. [A, s. 992]).
Toisen kertaluvun tilanteessa lause voidaan muotoilla seuraavasti:
Jos on yhtälön (H2) yksittäisratkaisu ja
yhtälön (E2) yksittäisratkaisu, niin
on myös yhtälön (E2) yksittäisratkaisu.
- Todistus sujuu samaan tapaan kuin 1. kl:n tilanteessa, ks. 3.2.3.
8.2 Epähomogeenisen DY:n yleinen ratkaisu
Lause:
Jos ja
ovat yhtälön (H2) lineaarisesti riippumattomia ratkaisuja
ja on yhtälön (E2) yksittäisratkaisu, niin yhtälön (E2) yleinen ratkaisu on
ja näin saadaan kaikki ratkaisut.
- Todistuksen ideat on nähty jo 1. kl:n tapauksessa kohdassa 3.2.3.
Huomautus:
- Kuten 1. kl:n tapauksessa, tämänkin lauseen voisi kirjoittaa myös toisessa muodossa:
Joson yhtälön (H2) yleinen ratkaisu ja
yhtälön (E2) yksittäisratkaisu, niin yhtälön (E2) yleinen ratkaisu on
ja näin saadaan yhtälön (E2) kaikki ratkaisut.
- Tässä siis vapaat vakiot ovat piilossa (epämääräisen) ilmaisun "
on yleinen ratkaisu" takana.
- Tässä siis vapaat vakiot ovat piilossa (epämääräisen) ilmaisun "
8.3 Epähomogeenisen DY:n yksittäisratkaisun löytämisestä
Kuten 1. kl:n tapauksessa, yksittäisratkaisua voidaan etsiä
- "valistuneen arvauksen" avulla
- jos yhtälö on vakiokertoiminen ja epähomogeeninen osa on tähän sopiva
- (arvauksen eli yritteen muoto perustuu epähomogeenisen osan muotoon, tarkemmin myöhemmin);
- jos yhtälö on vakiokertoiminen ja epähomogeeninen osa on tähän sopiva
tai
- vakioiden varioinnin avulla.
- Tämä on hiukan monimutkaisempaa kuin 1. kl:n tapauksessa, koska vakioita on kaksi - tarvitaan kaksi yhtälöä, joista vain toinen saadaan alkuperäisestä DY:stä, toinen pitää "määrätä".
- Tästä lisää myöhemmin.
- Tämä on hiukan monimutkaisempaa kuin 1. kl:n tapauksessa, koska vakioita on kaksi - tarvitaan kaksi yhtälöä, joista vain toinen saadaan alkuperäisestä DY:stä, toinen pitää "määrätä".
8.4 Epähomogeenisen yhtälön yksittäisratkaisu valistuneen arvauksen avulla (vakiokertoiminen yhtälö)
Tavoite: löytää jokin yhtälön (E2) eli toteuttava yksittäisratkaisu, kun
ja
ovat vakiofunktioita.
- Strategia:
- Arvataan ensin yksittäisratkaisun muoto funktion
perusteella ja käytetään vapaita kertoimia.
- Kuten aiemmin, tätä voidaan kutsua yritteeksi.
- (Yritteeksi voidaan kutsua mitä tahansa funktiota, jonka muoto on jotakin vapaata osaa lukuunottamatta määrätty ja jonka vapaa osa halutaan määrätä niin, että funktio toteuttaa annetun yhtälön.)
- Kuten aiemmin, tätä voidaan kutsua yritteeksi.
- Selvitetään kertoimet, joilla yrite toteuttaa yhtälön (E2).
- Arvataan ensin yksittäisratkaisun muoto funktion
- Vinkkejä yksittäisratkaisun muodon arvaamiseen, kun kerroinfunktiot
ja
ovat vakioita
- ja yrite ei satu olemaan vastaavan homogeenisen yhtälön ratkaisu:
| yrite | |
|---|---|
| polynomi | polynomi (samaa astetta) |
- Lisää vinkkejä:
- Jos
on jokin edellisistä kerrottuna
-asteisella polynomilla, korvataan yritteessä olevat vapaat kertoimet
ja
-asteisilla polynomeilla vapain kertoimin.
- Jos
on jokin edellisistä kerrottuna tekijällä
, kerrotaan myös yrite tällä tekijällä.
- Jos näin saatu yrite sattuu olemaan vastaavan homogeenisen yhtälön ratkaisu, kerrotaan yrite tekijällä
- tai, jos tämäkin on HY:n ratkaisu, tekijällä
.
- Jos
Huomautus:
- Kuten aiemmin, jos
ja/tai
ei ole vakiofunktio tai
ei sovi mihinkään edellä mainituista kuvauksista, yksittäisratkaisua voidaan etsiä homogeenisen yhtälön yleisen ratkaisun vakioiden varioinnilla.
- Tästä lisää myöhemmin.
8.5 Esimerkkejä
- Ratkaise
- Ratkaistaan ensin vastaava HY eli
karakteristisen yhtälön
avulla.
- Karakteristisen yhtälön ratkaisut ovat
ja
, joten HY:n yleinen ratkaisu on
- Karakteristisen yhtälön ratkaisut ovat
- Etsitään sitten epähomogeenisen DY:n
yksittäisratkaisu yritteen
avulla:
joten
Jotta DY
toteutuisi, pitää olla
josta saadaan
ja
.
- Löydettiin yksittäisratkaisu
.
- Löydettiin yksittäisratkaisu
- DY:n yleinen ratkaisu on
- Ratkaise
.
- HY:
, karakteristinen yhtälö:
- HY:n yleinen ratkaisu on
- HY:n yleinen ratkaisu on
- Etsitään yksittäisratkaisu yritteellä
:
joten
- Yksittäisratkaisuksi kelpaa
.
- Yksittäisratkaisuksi kelpaa
- Yleinen ratkaisu on
- Ratkaise
.
- HY sama kuin edellisessä, yleinen ratkaisu on
- Etsitään yksittäisratkaisu yritteellä
:
- (Huomaa, että
on HY:n ratkaisu eikä siksi toteuta epähomogeenista yhtälöä.)
ja
joten
ja DY toteutuu, kun
ja
eli
ja
.
- Yksittäisratkaisuksi kelpaa
.
- (Huomaa, että
- Yleinen ratkaisu on
- Ratkaise
.
- Kahdessa aiemmassa esimerkissä on löydetty
- HY:n
yleinen ratkaisu sekä
- epähomogeenisten yhtälöiden
ja
yksittäisratkaisut.
- HY:n
- Koska nyt HY on sama ja epähomogeeninen osa
on edellisten yhtälöiden epähomogeenisten osien summa, edellisten epähomogeenisten yhtälöiden yksittäisratkaisujen summa
on epähomogeenisen yhtälön
yksittäisratkaisu.
- (Tarkista itse.)
- Yleinen ratkaisu on
Huomautus
- Esimerkissä 3 yllä huomattiin, että yhtälön
yksittäisratkaisu on
- Kertoimen
vuoksi tämä ei ole rajoitettu funktio!
- Vrt. resonanssi, värähtelyä voimistetaan "samalla taajuudella".
- Kertoimen
8.6 Sovellus: harmoninen värähtelijä
Monet luonnonilmiöt ovat jaksollisia - esim. heiluriliike, kitaran kielen tai rummun kalvon värähtely, maailmanpyörän vaunun korkeus, kelluvan poijun liike meressä, vaihtovirran jännite...
Näissä ilmiöissä jokin suure (esim. maailmanpyörän vaunun korkeus ala-asentoon nähden) riippuu ajasta jaksollisesti, ja niinpä sini- ja kosinifunktiot sopivat ilmiön mallintamiseen. Muuttujana malleissa on aika, jota merkitään usein kirjaimella (time).
Malli perustuu luonnonlakeihin tai muuhun matematiikan ulkopuoliseen tietoon tai oletukseen ilmiöstä, esim. Newtonin lait fysiikassa, populaation kasvua rajoittavat (esim. ravinnon saantiin liittyvät) tekijät biologiassa tai hinnan vaikutus kysyntään taloustieteessä; usein suureeseen vaikuttaa jonkinlainen "tasapainotilan suuntaan vetävä voima", josta päädytään differentiaaliyhtälömalliin.
Yksinkertaisimmassa tällaisessa mallissa tasapainottava voima on verrannollinen poikkeamaan tasapainotilasta, mikä johtaa sinimuotoiseen edestakaiseen heilahteluun tasapainoaseman ympärillä. Tällaista mallia kutsutaan harmoniseksi värähtelijäksi.
8.6.1 Harmoninen värähtelijä
Harmonisen värähtelijän DY on eli
- Tausta:
- Kun punnus, jonka massa on
, riippuu (massattomasta) jousesta, punnukseen kohdistuu toisaalta painovoima ja toisaalta jousen kannatteleva voima; tasapainotilassa nämä ovat yhtä suuret.
- Kun merkitään funktiolla
punnuksen keskipisteen korkeutta tasapainotilaan nähden (eli tasapainotilassa
) ja oletetaan, että punnukseen kohdistuva voima on verrannollinen poikkeamaan tasapainotilasta, saadaan Newtonin laista "voima = massa * kiihtyvyys" yhtälö
- Verrannollisuuskerrointa
kutsutaan jousen jousivakioksi.
- Muistutus: nopeus on paikan ensimmäinen derivaatta ajan suhteen, kiihtyvyys toinen.
- Verrannollisuuskerrointa
- Jakamalla massalla ja merkitsemällä
saadaan yllä oleva harmonisen värähtelijän DY.
- Kun punnus, jonka massa on
Harmonisen värähtelijän DY:llä on yleinen ratkaisu joka voidaan esittää myös pelkän sinin tai pelkän kosinin (ja vaihesiirron) avulla:
kun
ja
, ja tällöin
ja
.
(Tämä seuraa suoraan kosinin summakaavasta.)
- Alkuehdot ja vakiot:
,
- (Tarkista itse.)
- Vakiot
ja
liittyvät siis punnuksen paikkaan ja nopeuteen alkuhetkellä
.
- Huomaa, että jos punnus on alkuhetkellä paikallaan tasapainoasemassa, se pysyy siinä (nollaratkaisu).
- Vakio
on liikkeen amplitudi eli ääriaseman etäisyys tasapainoasemasta.
- Aika, joka kuluu ääriasennosta paluuseen takaisin samaan ääriasentoon, on funktion
(perus)jakso
.
- Sama aika kuluu minkä tahansa peräkkäisten ajanhetkien välissä, jolloin punnus on samalla korkeudella ja liikkumassa samaan suuntaan (ylös tai alas).
- Jakson (aika
sekunteina) käänteisluku
on värähtelyn taajuus (hertseinä, 1 Hz = 1/s).
- Kulmataajuus on
(radiaania sekunnissa).
- Kulmataajuus on
Esimerkkejä
- Mitkä ovat ratkaisun amplitudi, taajuus ja jakso, kun värähtelijän DY on
ja alkuehdot
,
? (Ajan yksikkönä on sekunti.)
- Yleinen ratkaisu on
.
- Alkuehdoista saadaan
ja
eli
.
- Ratkaisu on siis
.
- Amplitudi on
. (Yksikköä ei ole annettu.)
- Taajuus on
Hz ja jakson pituus
sekuntia.
- Yleinen ratkaisu on
- Jousessa roikkuu 100 gramman punnus, jonka poikkeuttamiseen
cm tasapainoasemasta tarvitaan 30000
voima. Alkuhetkellä punnus vedetään 2 cm tasapainoaseman alapuolelle ja lähetetään ylöspäin nopeudella 60
. Mikä on punnuksen paikka hetkellä
? Entä kuinka kaukana tasapainoasemasta punnus käy?
- Punnuksen paikkaa hetkellä
kuvaava funktio
toteuttaa DY:n
missä
(
massa,
jousivakio).
- Selvitetään ensin jousivakio
annetusta tiedosta
(voima, joka tarvitaan kumoamaan punnukseen kohdassa
cm vaikuttava jousivoima
):
josta saadaan
.
- Kulmataajuus on
.
- Yleinen ratkaisu on
.
- Yleinen ratkaisu on
- Alkuehdot ovat
(cm) ja
(cm/s).
- Alkuehdot toteuttava ratkaisu on
.
- Alkuehdot toteuttava ratkaisu on
- Amplitudi on
cm.
8.6.2 Vaimennettu harmoninen värähtelijä
Kun harmonisen värähtelijän DY:öön lisätään vaimennuskerroin , saadaan mukaan ensimmäisen kertaluvun termi, mutta edelleen yhtälö on toisen kertaluvun lineaarinen homogeeninen vakiokertoiminen DY eli
(kertoimet
).
Harmoninen värähtelijä on
- alivaimennettu, jos
- eksponentiaalisesti vaimeneva heilahtelu
- kriittisesti vaimennettu, jos
- vaimenee nopeimmin, ei heilahtele
- ylivaimennettu, jos
- lähenee tasapainotilaa, mutta hitaammin kuin kriitisesti vaimennettu.
8.6.3 Pakotettu harmoninen värähtelijä
Kun (mahdollisesti vaimennetun) harmonisen värähtelijän DY:öön lisätään ulkoinen ajava voima , saadaan toisen kertaluvun epähomogeeninen lineaarinen vakiokertoiminen DY
- Yksinkertaisimmillaan
tai
,
- sinimuotoinen ajava voima, jonka kulmataajuus on
.
- sinimuotoinen ajava voima, jonka kulmataajuus on
- Vrt. keinu ja "vauhdin antaminen"; jos taajuus on oikea, amplitudi kasvaa (resonanssi).
9. Lineaarinen DY, osa V: 2. kl. lin. (yleisestä)
- Kertausta (lyhyesti):
- yleisen lineaarisen
- HY:n ratkaisukanta
- epähomogeenisen DY:n yleinen ratkaisu
- vakiokertoimisen lineaarisen
- HY karakteristisen yhtälön avulla
- epähomogeenisen yksittäisratkaisu valistuneella arvauksella
- yleisen lineaarisen
- Uutta:
- HY:n toinen ratkaisu kertaluvun pudotuksella
- epähomogeenisen DY:n yksittäisratkaisu vakioiden varioinnilla
9.0.1 Kertausta
Käytetään edelleen merkintää (E2) lineaarisesta 2. kertaluvun epähomogeenisesta differentiaaliyhtälöstä ja merkintää (H2) sitä vastaavasta homogeenisesta yhtälöstä
- Yhtälön (H2) yleinen ratkaisu:
- Jos
ja
ovat kaksi yhtälön (H2) lineaarisesti riippumatonta ratkaisua, niin yhtälön (H2) yleinen ratkaisu on
- Näin saadaan yhtälön (H2) kaikki ratkaisut.
- Funktiot
ja
muodostavat yhtälön (H2) ratkaisukannan.
- Jos
- Yhtälön (E2) yleinen ratkaisu:
- Jos
on yhtälön (H2) yleinen ratkaisu ja
yhtälön (E2) yksittäisratkaisu, niin yhtälön (E2) yleinen ratkaisu on
- Näin saadaan yhtälön (E2) kaikki ratkaisut.
- Vapaat vakiot ovat mukana merkinnässä
.
- Jos
- Jos kerroinfunktiot
ja
ovat vakiofunktioita, niin
- yhtälön (H2) ratkaisukanta löytyy karakteristisen yhtälön avulla
- yhtälön (E2) yksittäisratkaisu voi löytyä valistuneesti arvatun yritteen avulla.
9.1 HY:n ratkaisukannan etsiminen kertaluvun pudotuksella
Miten löydetään kaksi homogeenisen yhtälön (H2) ratkaisua, jotka ovat LI?
- Yksi ratkaisu on usein löydettävissä (/löydettävä) kokeilemalla.
- Kun on löydetty yksi yhtälön (H2) ratkaisu
, etsitään toinen yritteellä
9.1.1 Esimerkkejä
- Osoita, että
on yhtälön
ratkaisu ja etsi tästä lineaarisesti riippumaton ratkaisu yritteellä
(käyttämättä karakteristista yhtälöä). Mikä on yhtälön yleinen ratkaisu?
- Ratkaisu:
- Kun
, niin
ja
,
joten- Siis
on yhtälön
(eräs) ratkaisu.
- Siis
- Etsitään toinen ratkaisu yritteellä
- Tulon derivointissäännön mukaan
ja
- Jotta
toteuttaisi yhtälön
, täytyy siis olla
Tämä toteutuu, kun
eli kun
missä
ja
ovat vakioita; valitsemalla esim.
ja
saadaan
ja siis
- Koska
ei ole vakio, funktiot
ja
ovat LI.
- Löydettiin kaivattu toinen ratkaisu
, joka on lineaarisesti riippumaton funktiosta
.
- Löydettiin kaivattu toinen ratkaisu
- Tulon derivointissäännön mukaan
- Yleinen ratkaisu on
- Kun
- Osoita, että
on yhtälön
ratkaisu, ja selvitä yhtälön yleinen ratkaisu.
- Ratkaisu:
- Kun
, niin
ja
, joten
kaikilla
eli
on yhtälön (yksittäis)ratkaisu.
- Etsitään toinen ratkaisu yritteellä
:
- Tulon derivointissäännön mukaan
ja
- Jotta
toteuttaisi yhtälön
, täytyy siis olla
kaikilla
. Tämä toteutuu, kun
eli kun funktio
toteuttaa yhtälön
- Separoimalla (tai vaikka kokeilemalla) löydetään yksittäisratkaisu
, josta edelleen
.
- Saadaan siis
, joka on lineaarisesti riippumaton funktiosta
.
- Separoimalla (tai vaikka kokeilemalla) löydetään yksittäisratkaisu
- Löydettiin toinen ratkaisu
.
- Tarkista itse, että
on ratkaisu.
- Tarkista itse, että
- Tulon derivointissäännön mukaan
- Yleinen ratkaisu väleillä
ja
on
- Kun
9.1.2 Huomautuksia
- Esimerkeissä 1 ja 2 etsittiin homogeeniselle yhtälölle (H2) toinen ratkaisu yritteellä
missä
on ensin löydetty ratkaisu.
- Menetelmästä käytetään joskus nimitystä kertaluvun pudotus.
- Menetelmä johtaa ensimmäisen kertaluvun yhtälöön funktion
suhteen.
- Laske itse: jos
, niin
kun
on yhtälön
(yksittäis)ratkaisu.
- Laske itse: jos
- Menetelmä johtaa ensimmäisen kertaluvun yhtälöön funktion
- Menetelmä toimii, kun
kaikilla
(tutkittavalla välillä).
- Kiinnostuneet löytävät menetelmän toimivuudelle yleisen perustelun esim. P. Juutisen luentomonisteesta (s. 34); saadun toisen ratkaisun lineaarinen riippumattomuus ensimmäisestä voidaan tutkia nk. Wronskin determinantin avulla.
- Menetelmästä käytetään joskus nimitystä kertaluvun pudotus.
- Samalla menetelmällä löydettäisiin myös yleisesti vakiokertomiselle yhtälölle
jolle
(eli jonka karakteristisella yhtälöllä
on kaksoisjuuri
), yhden ratkaisun
avulla toinen ratkaisu
.
- Kokeile itse, lasku on sama kuin esimerkissä 1; huomaa, että nyt
ja
.
- (Oikeastaan saadaan
; voidaan valita
ja
vapaasti, kunhan ei valita
, jolloin tulos ei olisi enää LI funktion
kanssa.)
- (Oikeastaan saadaan
- Kokeile itse, lasku on sama kuin esimerkissä 1; huomaa, että nyt
9.2 Vakioiden variointi
Etsitään epähomogeenisen yhtälön (E2) yksittäisratkaisu yritteellä missä
ja
ovat vastaavan homogeenisen yhtälön (H2) kaksi lineaarisesti riippumatonta ratkaisua.
- Tehdään lisäoletus
- Tämä yksinkertaistaa laskuja.
- (E2) antaa vain yhden funktioita
ja
koskevan yhtälön, toinen voidaan valita.
9.2.1 Esimerkkejä
- Etsi yhtälölle
yksittäisratkaisu vakioiden varioinnilla.
- Ratkaisu:
- Vastaavan homogeenisen yhtälön
yleinen ratkaisu on
(tämä löydetään esim. karakteristisen yhtälön
ja sen kaksoisjuuren
avulla).
- Vakioiden variointi:
- Tehdään yrite
jolloin
- Tehdään lisäoletus
jolloin
ja
- Lisäoletusta käytettiin jälleen viimeisessä vaiheessa.
- (Ilman lisäoletusta saataisiin monimutkaisempi lauseke toisine derivaattoineen.)
- Jotta
olisi yhtälön ratkaisu, täytyy olla
eli
, josta saadaan
(integroimisvakio voidaan valita nollaksi).
- Yhtälön
perusteella
eli
joten
.
- Tehdään yrite
- Löydettiin yksittäisratkaisu
- Vrt. ratkaisu suoraan yritteen
avulla kuten H4/T8b:
ja on oltava
josta ratkaistaan
.
- Vastaavan homogeenisen yhtälön
- Ratkaise
välillä
.
- Ratkaisu:
- Vastaavan homogeenisen yhtälön
yleinen ratkaisu on
joka löydetään karakteristisen yhtälön
kompleksisten juurten
avulla.
- Etsitään epähomogeenisen yhtälön yksittäisratkaisu vakioiden varioinnilla.
- Tehdään yrite
ja lisäoletus
Nyt
ja
- Jotta yhtälö toteutuu, on oltava
ja yhdessä lisäoletuksen kanssa saadaan yhtälöpari
Ensimmäisestä saadaan
ja edelleen toisesta yhtälöstä
eli
jolloin
- Integroimalla (ja valitsemalla integroimisvakiot nolliksi) saadaan
ja
- Integraalin
laskeminen onnistuu sijoituksen
avulla, jolloin (ks. Calculus 3)
ja
sekä
; käyttäen myös trigonometrisia kaavoja saadaan
- Integraalin
- Löydettiin yksittäisratkaisu
- Tehdään yrite
- Yhtälön yleinen ratkaisu on
- Vastaavan homogeenisen yhtälön
9.2.2 Huomautuksia
- Vakion/vakioiden varioinnilla viitataan yleensä menetelmään, jossa yritteenä käytetään homogeenisen yhtälön ratkaisua, jossa vakion/vakioiden paikalle laitetaan funktio(t).
- Tässä mielessä myös aiemmin nähty kertaluvun pudotus -menetelmä homogeenisen yhtälön toisen ratkaisun löytämiseksi on "vakion variointia".
- Vakioiden variointi soveltuu myös korkeampien kertalukujen yhtälöille, mutta voi johtaa hankaliin laskuihin.
10. Korkeamman kertaluvun DY:istä ynnä muuta
- korkeamman kertaluvun lineaarinen DY
- erikoistapauksia:
- vakiokertoiminen lin. homogeeninen
- Eulerin yhtälö (2. kl)
[A, 18.5]
10.1 Lineaarinen korkeamman kertaluvun DY
Tarkastellaan nyt lineaarista :nnen kertaluvun epähomogeenista differentiaaliyhtälöä
ja sitä vastaavaa homogeenista yhtälöä
Oletetaan, että kerroinfunktiot
ovat jatkuvia ja
koko tutkittavalla välillä.
- Jos
ovat yhtälön (Hn) lineaarisesti riippumattomia ratkaisuja, niin yhtälön (Hn) yleinen ratkaisu on
ja näin saadaan kaikki ratkaisut.
- Jos
on yhtälön (Hn) yleinen ratkaisu ja
yhtälön (En) yksittäisratkaisu, niin yhtälön (En) yleinen ratkaisu on
ja näin saadaan yhtälön (En) kaikki ratkaisut.
- Kuten aiemmin, vapaat vakiot ovat piilossa (epämääräisen) ilmaisun "
on yleinen ratkaisu" takana.
- Kuten aiemmin, vapaat vakiot ovat piilossa (epämääräisen) ilmaisun "
10.2 Vakiokertoiminen n:nnen kl:n lineaarinen homogeeninen DY
Lineaarinen, homogeeninen, vakiokertoiminen :nnen kertaluvun DY on
missä
.
10.2.1 Karakteristinen yhtälö
Vastaavasti kuin toisen kertaluvun tilanteessa (ks. 7.3), myös kertaluvulle differentiaaliyhtälön (
) karakteristinen yhtälö on
- Differentiaaliyhtälön (
) ratkaisut löytyvät yhtälön (
) ratkaisujen eli juurten avulla.
- Tiedetään, että (kompleksiset sekä moninkertaiset juuret huomioiden)
:nnen asteen polynomiyhtälöllä on
juurta.
- DY:lle (
) löydetään sen karakteristisen yhtälön juurten avulla
yksittäisratkaisua, jotka ovat toisistaan lineaarisesti riippumattomia.
- DY:n (
) yleinen ratkaisu saadaan näiden ratkaisujen avulla vastaavasti kuin 2. kl:n tapauksessa.
- DY:n (
- Tiedetään, että (kompleksiset sekä moninkertaiset juuret huomioiden)
Perusteluksi / johdatteluksi:
- Etsitään ratkaisua yritteellä
jolloin
,
jne; yleisesti
:s derivaatta on
Yrite
on DY:n (
) ratkaisu, jos
eli jos
10.2.2 Vakiokertoimisen HY:n ratkaisut karakteristisen yhtälön avulla
- Tiedetään, että reaalikertoimisen polynomiyhtälön juuret ovat joko
- yksinkertaisia reaalijuuria,
- moninkertaisia reaalijuuria tai
- kompleksisia (yksin- tai moninkertaisia) juuria.
- Kompleksiset juuret esiintyvät aina pareina kompleksikonjugaattinsa kanssa; siis
joson
-kertainen juuri, niin
myöson
-kertainen juuri.
- Vrt. polynomin jako 1. ja 2. asteen tekijöihin.
- Kompleksiset juuret esiintyvät aina pareina kompleksikonjugaattinsa kanssa; siis
- Reaalijuuret:
- Jos
on yhtälön (
)
-kertainen reaalinen juuri
(elion polynomin
tekijä),
niin funktiotovat yhtälön (
) LI ratkaisuja.
- (
kpl)
- (
- Jos
- Kompleksijuuret:
- Jos
ja
ovat yhtälön (
)
-kertaisia kompleksisia juuria
(elion polynomin
tekijä),
niin funktiotja
ovat yhtälön (
) LI ratkaisuja.
- (
kpl)
- (
- Jos
10.2.3 Esimerkkejä
- Ratkaise
.
- Ratkaisu:
- Karakteristinen yhtälö on
- Jaetaan polynomi
tekijöihin:
- Tästä nähdään, että yhtälöllä
on juuret eli ratkaisut
,
,
ja
(neljä yksinkertaista juurta).
- Jaetaan polynomi
- Yhtälön
yleinen ratkaisu on
- Karakteristinen yhtälö on
- Ratkaise
.
- Ratkaisu:
- Karakteristinen yhtälö on
- Jaetaan polynomi
tekijöihin:
- Tästä nähdään, että yhtälöllä
on juuret 0, 0, 0, 1 ja 1 eli
- kolminkertainen juuri
ja
- kaksinkertainen juuri
.
- kolminkertainen juuri
- Jaetaan polynomi
- Yhtälön
yleinen ratkaisu on
- Karakteristinen yhtälö on
- Selvitä DY:n kertaluku ja yleinen ratkaisu, kun DY on lineaarinen, homogeeninen ja vakiokertoiminen, ja sen karakteristinen yhtälö on
- Ratkaisu:
- Karakteristinen yhtälö
on 7. asteen polynomiyhtälö, joten DY:n kertaluku on 7.
- Karakteristisella yhtälöllä on
- kolminkertainen juuri
sekä
- kaksinkertaiset kompleksiset juuret
.
- kolminkertainen juuri
- DY:n yleinen ratkaisu on
.
- Karakteristinen yhtälö
10.3 Eulerin yhtälö (2. kl)
Yhtälöä missä
(ja missä
on muuttujan
funktio kuten aiemminkin),
kutsutaan (2. kertaluvun) Eulerin yhtälöksi.
- Jakamalla yhtälö lausekkeella
saataisiin normaalimuotoinen lineaarinen yhtälö
kun
, joka ei ole määritelty, kun
.
- Etsitään ratkaisua, kun
. (Sama ratkaisu kelpaa myös, kun
, kun korvataan
lausekkeella
.)
- Etsitään ratkaisua, kun
10.3.1 Karakteristinen yhtälö
- Etsitään Eulerin yhtälölle
ratkaisua välillä
yritteellä
.
- Koska
niin
on yhtälön ratkaisu, jos
kaikilla
eli jos
eli jos
- Koska
Eulerin yhtälön (Eu) ratkaisut löydetään tämän karakteristisen yhtälön avulla.
- Kaksi reaalijuurta:
- Jos
, niin yhtälöllä
on kaksi reaalijuurta,
ja
,
.
- Tällöin Eulerin yhtälöllä (Eu) on välillä
yleinen ratkaisu
- Yleinen ratkaisu voidaan kirjoittaa muodossa
joka on ratkaisu myös välillä
.
- (Tarkista itse, että on ratkaisu, kun
.)
- (Tarkista itse, että on ratkaisu, kun
- Jos
- Yksi kaksinkertainen reaalijuuri:
- Jos
, niin yhtälöllä
on kaksinkertainen reaalijuuri
.
- Tällöin Eulerin yhtälöllä (Eu) on välillä
yleinen ratkaisu
- Ratkaisu
löydetään kertaluvun pudotuksella, ks. 9.1. (laske itse).
- Ratkaisu
- Yleinen ratkaisu voidaan kirjoittaa muodossa
joka on ratkaisu myös välillä
.
- Jos
- Kompleksiset juuret:
- Jos
, niin yhtälöllä
on kaksi kompleksijuurta,
ja
.
- Tällöin Eulerin yhtälöllä (Eu) on välillä
yleinen ratkaisu
- Yleinen ratkaisu voidaan kirjoittaa muodossa
joka on ratkaisu myös välillä
.
- Jos
Eulerin yhtälöiden ratkaisuun käytettävässä yhtälössä virhe. Virheellinen: ar^2-(b-a)r+c=0. Oikein: ar^2+(b-a)r+c=0 (kuten ylempänä on kirjoitettu)
—Kiitos, korjattu.
—- Toinen tapa:
- Eulerin yhtälö (Eu) voidaan ratkaista myös palauttamalla se vakiokertoimiseksi DY:ksi muuttujanvaihdon
avulla.
- Tällöin päädytään yhtälöön
,
missä.
- Tällöin päädytään yhtälöön
- Eulerin yhtälö (Eu) voidaan ratkaista myös palauttamalla se vakiokertoimiseksi DY:ksi muuttujanvaihdon
10.3.2 Esimerkkejä
- Ratkaise alkuarvotehtävä
,
,
.
- Ratkaisu:
- Karakteristinen yhtälö on
eli
- Karakteristisella yhtälöllä on kaksi reaalijuurta,
ja
.
- Karakteristisella yhtälöllä on kaksi reaalijuurta,
- Yleinen ratkaisu välillä
on
- Alkuehtojen toteutuminen:
- Koska
, alkuehdoista saadaan yhtälöpari
ja sen ratkaisuna
ja
.
- Alkuehdot toteuttava ratkaisu on siis
- Koska
- Karakteristinen yhtälö on
- Ratkaise
.
- Ratkaisu:
- Karakteristinen yhtälö on
eli
- Karakteristisella yhtälöllä on kaksi kompleksijuurta,
.
- Karakteristisella yhtälöllä on kaksi kompleksijuurta,
- Yleinen ratkaisu on
- Karakteristinen yhtälö on
11. Sarjaratkaisuista, osa I
- Potenssisarja ja analyyttinen funktio
- Lineaarisen 2. kl:n DY:n potenssisarjamuotoisen ratkaisun etsiminen
- rekursioyhtälö sarjan kertoimille
[A, 18.7] ja [B, luku 4]
11.1 Potenssisarjoista
Tarkastellaan potenssisarjaa jonka
- kertoimet
ovat reaalilukuja
- kehityskeskus on
- suppeneminen tarkoittaa raja-arvon
olemassaoloa.
- Huom: riippuu muuttujan
arvosta!
- Huom: riippuu muuttujan
Sarjoihin liittyvät perusasiat voit tarvittaessa kerrata esim. kurssilta Calculus 3:
- lukusarjan suppeneminen ja itseinen suppeneminen
- lukusarjan suppenemistestit
- potenssisarjan suppenemissäde ja suppenemisväli
- suppenemissäteen etsiminen suppenemistestien avulla
- potenssisarjojen yhteen-, vähennys- ja kertolasku (Cauchyn tulo)
- potenssisarjan derivointi ja integrointi
- termeittäin; suppenemissäde ei muutu
- funktion Taylorin sarja ja analyyttisyys kerrataan alla
- käytössä tavanomaiset merkinnät
,
,
- käytössä tavanomaiset merkinnät
11.2 Analyyttinen funktio
Jos kaikilla
jollakin
, niin sanomme, että funktio
on analyyttinen kohdassa
.
- Tällöin
- kertoimet ovat
ja
- sarjaa kutsutaan funktion
Taylorin sarjaksi kehitettynä pisteessä
.
- kertoimet ovat
Esimerkkejä:
- Lisää sarjakehitelmiä löytyy esim. Ari Lehtosen kaavakokoelmasta:
http://users.jyu.fi/~lehtonen/opetus/TrigKaavoja_v3.pdf
Huomioita:
- Jos kehityskeskus muuttuu, myös kertoimet muuttuvat, esim.
kaikilla
; siis
kaikilla
.
- Polynomit ovat analyyttisiä; polynomin Taylorin sarja on päättyvä
(eli jostakin alkaen loput kertoimet ovat nollia). - Rationaalifunktiot ovat analyyttisiä määrittelyjoukkonsa pisteissä, mutta Taylorin sarjan suppenemissäde voi olla pienikin, esim.
- (huomaa nimittäjän kompleksinen nollakohta
)
- (huomaa nimittäjän kompleksinen nollakohta
- Jos funktio on analyyttinen, niin sillä on kaikkien kertalukujen derivaatat.
- Toinen suunta ei ole totta; vastaesim.
, kun
ja
, joka ei ole analyyttinen origossa.
- Toinen suunta ei ole totta; vastaesim.
- Analyyttisten funktioiden summat, tulot ja yhdistetyt funktiot ovat myös analyyttisiä.
- Siellä, missä potenssisarja suppenee, se määrittelee analyyttisen funktion
- jolla ei välttämättä ole lauseketta "suljetussa muodossa" eli alkeisfunktioiden avulla.
11.3 Johdattelevia esimerkkejä
- Etsitään yhtälölle
ratkaisua sarjan
muodossa eli etsitään sellaiset kertoimet
, että
on yhtälön ratkaisu.
- Ratkaisu:
- Potenssisarja voidaan derivoida termeittäin, joten
ja
- Jotta yhtälö toteutuu, on oltava
eli (tehdään ensimmäiselle sarjalle indeksin siirto; vrt. muuttujanvaihto
)
- Tämä toteutuu kaikilla
vain silloin, kun saadun sarjan jokainen kerroin on nolla; siis
kaikilla
- Kaksi sarjan
ensimmäistä kerrointa ovat
ja
(vapaita), muut saadaan laskettua näistä:
jne; yleisesti saadaan parillisen (
) ja parittoman (
) indeksin kertoimille oma kaavansa:
kun
- Tämä toteutuu kaikilla
- Kiinnittämällä kertoimet
ja
saadaan yksittäisratkaisuja:
- valitsemalla
ja
saadaan
- valitsemalla
ja
saadaan
- Eri valinnoilla saadaan LI ratkaisut, joten yleinen ratkaisu saadaan näiden avulla.
- valitsemalla
- DY:n yleinen ratkaisu on
.
- Vrt. ratkaisu karakteristisen yhtälön avulla aiemmin:
.
- Vrt. ratkaisu karakteristisen yhtälön avulla aiemmin:
- Potenssisarja voidaan derivoida termeittäin, joten
- Etsi esimerkin 1 yhtälölle
ratkaisu, joka toteuttaa alkuehdot
,
.
- Ratkaisu:
- Esimerkissä 1 löydettiin sarjaratkaisu
- Koska
ja
, alkuehdot toteuttava ratkaisu on
- Saatiin siis
(kuten aiemmin opituilla keinoilla).
- Saatiin siis
- Esimerkissä 1 löydettiin sarjaratkaisu
Miksi y_s(0)=a_0 ja y’_s(0)=a_1? Jos teen x=0 sitten kaikki on nolla
AL: Huomaa, että vakiotermi (muuttujaosa \(x^0=1\)) ei ole nolla, kun x=0.
—11.4 Yleistä sarjaratkaisuista
- Johdattelevassa esimerkissä 11.3
- oletettiin, että differentiaaliyhtälöllä on ratkaisu muodossa
ja etsittiin sarjan kertoimia
koskeva ehto, jonka täyttyessä ko. sarja on DY:n ratkaisu;
- Yhtälöä
kutsutaan rekursioyhtälöksi.
- Yhtälöä
- saatiin kertoimia koskevasta rekursioyhtälöstä kertoimille yleinen kaava indeksin
sekä ensimmäisten kertomien (ja samalla alkuarvojen)
ja
avulla.
- (Itse asiassa saatiin eri kaavat parillisilla ja parittomilla indekseillä
; tämän vuoksi myös itse ratkaisu oli kätevää kirjoittaa yhden sarjan sijaan kahden sarjan summana.)
- (Itse asiassa saatiin eri kaavat parillisilla ja parittomilla indekseillä
- oletettiin, että differentiaaliyhtälöllä on ratkaisu muodossa
- Sivuhuomio:
- sinifunktio voitaisiin itse asiassa määritellä alkuarvotehtävän
,
,
ratkaisuna,
kosini vastaavasti tehtävän
,
,
ratkaisuna,
- ja johtaa näiden ominaisuudet DY:n ratkaisun sarjaesityksen avulla.
- sinifunktio voitaisiin itse asiassa määritellä alkuarvotehtävän
Voisiko näistä vaikka olla jokin esimerkki
AL: Yllä on yksi esimerkki, alempana toinen. Millaista lisäesimerkkiä kaipaisit?
#- Esimerkiksi, jokin hieman vaikeampi kuin yllä, mutta ei singulaaripisteen avulla
AL: Adamsin Calculus-kirjasta löytyy esimerkki, joka on vaikeampi kuin tuo yllä oleva (ja siksi otin mieluummin tuon yllä olevan). Braunin kirjasta, joka on mainittu lukemistolistassa Koti-sivulla, löytyy s. 186 Example 1, joka vastannee toiveitasi paremmin; sivulta 190 alkaen löytyy myös lisää esimerkkejä.
AL: Esimerkki 3 lisätty 28.4.2021
—- Yleisemmin lineaariselle 2. kertaluvun differentiaaliyhtälölle
voidaan etsiä sarjaratkaisua vastaavalla tavalla yritteellä
jolloin päädytään kertoimia
koskevaan rekursioyhtälöön.
- Ensimmäisten kertoimien kiinnittämisen jälkeen loput voidaan laskea yksi kerrallaan.
- Joskus kertoimille löydetään suora laskukaava (ilman rekursiota).
- Valitsemalla kehityspiste
eri tavalla päädytään hiukan eri laskuihin.
- Alkuarvotehtävässä valitaan kehityspisteeksi
se muuttujan arvo, jolle alkuarvot
ja
on annettu.
- Näin alkuehdot määräävät suoraan sarjan ensimmäiset kertoimet. (Miksi?)
- Huomaa, että tällöin myös kerroinfunktiot on ilmaistava binomin
potenssien avulla. (Miksi?)
- Muuttujanvaihdolla
voidaan toki palauttaa kehityspiste origoon, ratkaista saatu uusi DY ja lopuksi palata alkuperäiseen muuttujaan.
- Alkuarvotehtävässä valitaan kehityspisteeksi
- Kysymyksiä:
- Voidaanko aina olettaa, että yhtälöllä on ratkaisu ko. sarjamuodossa?
- Ainakin silloin, kun
kaikilla
jollakin
ja kerroinfunktiot ovat analyyttisiä (esim. polynomeja).
- Kiinnostuneet löytävät lisätietoja esim. [B, 3.1 ja 4].
- Jos
, tilanne on monimutkaisempi; tästä hiukan lisää myöhemmin.
- Ainakin silloin, kun
- Missä sarja suppenee, eli missä se määrittelee funktion, joka on DY:n ratkaisu?
- Tätä voidaan tutkia kurssilla Calculus 3 opituilla menetelmillä.
- Voidaanko aina olettaa, että yhtälöllä on ratkaisu ko. sarjamuodossa?
- TÄRKEÄÄ:
- Eri alojen, varsinkin fysiikan, ilmiöiden mallinnuksessa päädytään usein differentiaaliyhtälöihin, joilla tiedetään olevan ratkaisuja tai joille jopa löydetään ratkaisuja sarjamuodossa, mutta joiden ratkaisuilla ei ole lauseketta alkeisfunktioiden avulla.
- (Taustalla ratkaisujen olemassaolo- ja yksikäsitteisyyslauseet...)
- Sarjaesitys määrittelee suppenemisvälillään uuden funktion, jolle voidaan todistaa erilaisia ominaisuuksia.
- Vrt. integraalin avulla määritellyt funktiot kuten normaalijakauman kertymäfunktio.
- Arvoille voidaan laskea niin tarkkoja likiarvoja kuin halutaan.
- Joskus käytetään nimitystä "erikoisfunktio" - tosin nimitys ei ole tarkasti rajattu.
- Joillekin usein tarvittaville erikoisfunktioille on annettu nimiä kuten esim. Besselin funktiot.
- Eri alojen, varsinkin fysiikan, ilmiöiden mallinnuksessa päädytään usein differentiaaliyhtälöihin, joilla tiedetään olevan ratkaisuja tai joille jopa löydetään ratkaisuja sarjamuodossa, mutta joiden ratkaisuilla ei ole lauseketta alkeisfunktioiden avulla.
Esimerkki
- Etsi yhtälölle
kaksi LI ratkaisua.
- Ratkaisu:
- Tehdään sarjayrite
.
- Potenssisarja voidaan derivoida termeittäin, joten
ja
- Jotta yhtälö toteutuu, on oltava
- Tämä toteutuu kaikilla
vain silloin, kun saadun sarjan jokainen kerroin on nolla; siis
ja
kaikilla
eli
ja kun
,
- Tämä toteutuu kaikilla
- Valitaan kaksi sarjan
ensimmäistä kerrointa (jotka yleisessä ratkaisussa olisivat vapaita vakioita) kahdella eri tavalla kahden eri ratkaisun saamiseksi.
- Valitaan ensin
ja
, jolloin
Siis
(kaikki parittomien potenssien kertoimet ovat nollia, koska
, ja koska
, myös parillisten potenssien kertoimet ovat tästä alkaen nollia, ja siksi ratkaisu on polynomi).
- Valitaan sitten
ja
, jolloin
(samoin kaikki muutkin parillisten potenssien kertoimet) ja
yleisesti
eli
Näin saatiin toinen ratkaisu
Tämä on lineaarisesti riippumaton ensin löydetystä ratkaisusta
, joka oli polynomi.
- Valitaan ensin
- Tehdään sarjayrite
12. Sarjaratkaisuista, osa II
- Johdattelua
- DY:n singulaaripiste
- ratkaisun etsimisestä säännöllisen singulaaripisteen lähistöllä
[A, 18.7] ja [B, luku 4]
12.1 Johdattelua
Tarkastellaan 2. kl:n lineaarista homogeenista DY:ä missä kerroinfunktiot
ja
ovat analyyttisiä.
- Muistutus (mainittu luvussa 7): jos kerroinfunktiot
ja
ovat jatkuvia, normaalimuotoisen lineaarisen DY:n
alkuarvotehtävällä on yksikäsitteinen ratkaisu.
- Sivumaininta: yleinen ratkaisu löytyy pisteessä
kehitetyn potenssisarjan muodossa, jos
ja
ovat analyyttisiä pisteessä
.
- Sivumaininta: yleinen ratkaisu löytyy pisteessä
- Entä, jos kerroinfunktiolla
on nollakohtia? (Voiko yhtälöllä olla ratkaisuja myös välillä, joka sisältää
:n nollakohdan? Mitä voi tapahtua?)
Esimerkkejä/havaintoja
- Osoita, että
ja
ovat kaksi yhtälön
LI ratkaisua välillä
. Millä tavalla ratkaisut käyttäytyvät, kun
?
- Osoitus sijoittamalla kuten aiemmin. Huomataan, että ratkaisulla
on äärellinen raja-arvo nollassa, mutta ratkaisulla
ei.
- Lisähuomio: yleinen ratkaisu välillä, joka ei sisällä nollaa, on
(sama kuin normaalimuotoisella yhtälöllä
).
- Lisähuomio: yleinen ratkaisu välillä, joka ei sisällä nollaa, on
- Osoita, että
ja
ovat kaksi yhtälön
LI ratkaisua. Mikä on yhtälön yleinen ratkaisu? Piirrä muutamia ratkaisujen kuvaajia. Mitä huomaat?
- Osoitus sijoittamalla kuten aiemmin. Yhtälön yleinen ratkaisu on
(huomataan, että näistä jokainen saa nollassa arvon nolla; alkuehtoja ei siis voi asettaa nollassa, vaikka kukin ratkaisu on analyyttinen kaikkialla).
12.2 Singulaaripiste
Jos ja lisäksi
tai
, niin sanomme, että piste
on yhtälön
singulaaripiste.
- Käytetään vastaavan normaalimuotoisen yhtälön kertoimista merkintöjä
eli normaalimuotoinen yhtälö on
- Huomataan, että singulaaripisteen
lähistöllä kerroinfunktioista
ja
ainakin toinen on rajoittamaton (ts. toispuolinen epäoleellinen raja-arvo on
tai
) eli sillä on nk. singulariteetti tässä kohdassa; funktio ei ole jatkuva eikä jatkettavissa jatkuvasti kohtaan
.
Jos funktiot ovat
analyyttisiä kohdassa
, niin sanomme, että
on yhtälön säännöllinen singulaaripiste.
Tässä tulofunktiot jatketaan jatkuvasti määrittelemättömyyskohtaan
, jos mahdollista eli käytetään arvona raja-arvoa, jos äärellinen raja-arvo löytyy.
12.2.1 DY:n ratkaisu säännöllisen singulaaripisteen lähellä
Etsitään ratkaisua potenssisarjan sijaan muodossa missä
on DY:n säännöllinen singulaaripiste.
- Löydetään ainakin yksi ratkaisu; toista voi etsiä vaikkapa kertaluvun pudotuksella, joka tosin saattaa johtaa hankaliin laskuihin.
- Kiinnostuneet löytävät muitakin menetelmiä, esim. [B, 4.6].
- Esimerkkejä:
- Eulerin yhtälö
,
- johon tutustuttiin jo aiemmin kohdassa 10.3 sekä harjoituksissa H5/T8-9
- Besselin yhtälö
- jonka tapausta
käsiteltiin harjoituksissa H5/T10.
- jonka tapausta
- Eulerin yhtälö
Esimerkki
- Etsi Besselin yhtälölle
yksi ratkaisu muodossa
- Ratkaisu:
- Kun
niin
ja
- Jotta yhtälö toteutuisi, on oltava
kaikilla
.
- Koska voidaan valita kerroin
(
), saadaan vakiotermistä yhtälö
eli
tai
.
- (Jos olisi
, olisi termeillä yhteinen tekijä
, joka erotettaisiin tekijään
.)
- (Jos olisi
- Tällöin välttämättä ensimmäisen asteen termin kerroin
.
- Kun
, kertoimille saadaan rekursioyhtälö
eli
eli
- Koska voidaan valita kerroin
- Valitaan
, jolloin rekursioyhtälö on
- Koska
, saadaan
,
jne,
kaikilla
- Valinnalla
saadaan
ja yleisesti
- Koska
- Yksi DY:n ratkaisu on
- (Tarkista itse, että on ratkaisu.)
- Suhdetestin avulla nähdään, että sarja suppenee kaikilla
.
- Kun
Huomioita
- Jos indeksiyhtälön (yllä
) juurten erotus ei ole kokonaisluku, saadaan sijoittamalla juuret
ja
sarjaan
kaksi LI ratkaisua.
- (Kompleksijuurten tapauksessa ratkaisut ovat kompleksiarvoisia, mutta niiden avulla löydetään reaaliarvoiset LI ratkaisut kuten Eulerin yhtälölle; vrt. H5/T10.)
- Jos indeksiyhtälön juuret ovat samat tai poikkeavat toisistaan kokonaisluvun verran (kuten yllä
tai
), saadaan sijoittamalla suurempi juuri
sarjaan
yksi ratkaisu kuten yllä; toisessa ratkaisussa esiintyy lisäksi logaritmi.
- Kiinnostuneet löytävät lisätietoja muista lähteistä, esim. [B].
13. DY-systeemeistä, osa I
- Yleistä systeemeistä
- Lineaarinen 1. kl:n systeemi
- Yhteys korkeamman kertaluvun yhtälöihin
[B, 7.1 ja 7.2]
13.1 Yleistä DY-systeemeistä
13.1.1 Johdattelua ja merkintöjä
- Aiemmin on käsitelty differentiaaliyhtälöitä, joissa esiintyy yhden muuttujan funktio
, sen derivaattoja
,
jne. sekä mahdollisesti myös muuttujan
funktioita.
- Esim. 2. kl:n lineaarinen epähomogeeninen DY
- Tällainen yhtälö kuvaa yhden suureen (
) muuttumista toisen suureen, nk. riippumattoman muuttujan (
) suhteen.
- Usein muuttujana on aika; käytetään jatkossa riippumattomasta muuttujasta merkintää
.
- Esim. 2. kl:n lineaarinen epähomogeeninen DY
- Seuraavaksi tarkastellaan useamman suureen muuttumista kuvaavia yhtälöpareja ja -ryhmiä; merkitään tuntemattomia funktioita kirjaimilla
,
,
tai
,
,
jne. ja muuttujaa kirjaimella
.
- Derivaattojen merkitsemiseen voidaan käyttää tuttua "pilkkumerkintää", esim.
- Derivaattojen merkitsemiseen voidaan käyttää tuttua "pilkkumerkintää", esim.
13.1.2 Esimerkkejä ilmiöistä
- Jänisten ja kettujen määrää tietyllä alueella voi mallintaa DY-parilla
eli
missä
on jänisten määrä hetkellä
on kettujen määrä hetkellä
- parametri
on jänisten syntyvyys
- (populaatio kasvaa eksponentiaalisesti, jos kettuja ei ole)
- parametri
on kettujen kuolevuus
- (populaatio vähenee eksponentiaalisesti, jos jäniksiä ei ole)
- parametrit
ja
kuvaavat, miten jänisten ja kettujen määrät vaikuttavat toisiinsa.
- Tämä on nk. Lotkan ja Volterran peto-saalis -malli vuodelta 1925.
- Kappaleen paikkaa (
)-koordinaatistossa kuvaa systeemi
missä
on kappaleen massa,
on kappaleeseen vaikuttava voima,
- joka voi riippua sekä ajasta että kappaleen paikasta ja nopeudesta.
- Tausta:
- voima = massa
kiihtyvyys
- Newtonin laki
- koordinaattiakseleiden suuntaisiin komponentteihin hajotettuna
- kiihtyvyys = paikan 2. derivaatta ajan suhteen.
- voima = massa
- Kahden jousen ja kahden kappaleen kytketty systeemi
- (kiinteästä pisteestä alkaa jousi 1, jonka päässä on kappale 1, josta alkaa jousi 2, jonka päässä on kappale 2
- vaakasuorassa kitkattomalla pinnalla tai pystysuorassa, jolloin käsitellään jousivoiman ja painovoiman erotusta)
- Kappaleiden poikkeamat
ja
tasapainoasemasta riippuvat toisistaan:
missä
ja
ovat kappaleiden massat
ja
ovat jousien jousivakiot.
- Tausta:
- kappaleeseen vaikuttava voima on verrannollinen poikkeamaan tasapainoasemasta (ks. 8.6).
- Jos systeemiin lisätään ulkoinen voima
, joka kohdistuu kappaleeseen 2, saadaan systeemi
- (kiinteästä pisteestä alkaa jousi 1, jonka päässä on kappale 1, josta alkaa jousi 2, jonka päässä on kappale 2
- Kolmen jousen ja kahden kappaleen kytketty systeemi
- Vaakasuorassa kitkattomalla pinnalla kahden kiinteän pisteen välissä on
kolme jousta sekä näiden välissä kaksi kappaletta. - Kappaleisiin vaikuttavat ulkoiset voimat
ja
.
- Kappaleiden poikkeamat
ja
tasapainoasemasta riippuvat sekä toisistaan että ulkoisista voimista (vrt. esimerkki 3):
eli
- Vaakasuorassa kitkattomalla pinnalla kahden kiinteän pisteen välissä on
- Suolaliuosten sekoittuminen kahdessa tankissa, joiden välillä neste liikkuu:
- (ks. tarvittaessa yhden tankin tilanne H3/T9)
- Suolan määrä
tankissa 1 ja
tankissa 2 riippuvat toisistaan:
missä
ja
ovat tankkien tilavuudet
ja
ovat liuosten virtausnopeudet putkissa 1 (tankista 1 tankkiin 2) ja 2 (tankista 2 tankkiin 1)
- Tausta:
- Suolapitoisuus tankissa 1 on
ja tankissa 2 vastaavasti
.
- Oletetaan, että tankkien sisältöä "sekoitetaan hyvin" eli suola on koko ajan tasaisesti sekoittunut tankin sisällä.
- Suolamäärän muutos tankissa on ulosvirtauksen ja sisäänvirtauksen suolamäärien erotus.
- Suolapitoisuus tankissa 1 on
- Jos kierto ei ole suljettu,
- vaan esim.
- tankkiin 1 valutetaan suolatonta vettä nopeudella
ja
- tankista 2 valutetaan liuosta pois samalla nopeudella
,
- tankkiin 1 valutetaan suolatonta vettä nopeudella
- niin saadaan systeemi
eli
- vaan esim.
13.1.3 DY-systeemin ratkaisu ja alkuarvotehtävä
Kahden yhtälön 1. kertaluvun DY-systeemin (tai DY-parin) ratkaisulla tarkoitetaan funktioita
ja
, jotka (yhdessä) toteuttavat molemmat yhtälöt (jollakin välillä).
Vastaavasti 1. kl:n DY-systeemin ratkaisulla tarkoitetaan funktioita
, jotka toteuttavat kaikki
yhtälöä (jollakin välillä).
Alkuarvotehtävä muodostuu, kun DY-systeemin yhtälöiden lisäksi määrätään funktioiden arvot jossakin (yhdessä) pisteessä; esimerkin 1 tilanteessa esim.
Huomioita:
- DY-systeemissä voi esiintyä myös korkeamman kertaluvun differentiaaliyhtälöitä.
- Kertaluvun
lineaarinen DY voidaan muuttaa ensimmäisen kertaluvun DY-systeemiksi, jossa on
yhtälöä.
- Tästä lisää myöhemmin.
13.2 Lineaarinen DY-systeemi
Tällä kurssilla käsittelemme vain lineaarisia DY-systeemejä.
Yleinen yhtälön 1. kertaluvun lineaarinen DY-systeemi on muotoa
- Jos
ovat kaikki nollafunktioita, niin sanomme, että lineaarinen systeemi on homogeeninen, muutoin epähomogeeninen.
- Jos funktiot
ja
ovat jatkuvia jollakin välillä, niin vastaavalla alkuarvotehtävällä on yksikäsitteinen ratkaisu tällä välillä.
- Kuten yhden yhtälön tapauksessa on nähty, myös epähomogeenisen DY-systeemin yleinen ratkaisu löytyy vastaavan homogeenisen systeemin yleisen ratkaisun ja epähomogeenisen systeemin yksittäisratkaisun avulla.
- Tapausta
käsitellään tehtävässä H7/T8.
- Tapausta
- Yllä nähdyissä esimerkeissä
- lineaarisia olivat systeemit esimerkeissä 3, 4 ja 5
- esimerkin 2 systeemin lineaarisuus riippuu funktioista
,
ja
- esimerkin 1 Lotkan ja Volterran peto-saalis -malli
on esimerkki epälineaarisesta DY-systeemistä.
- Tällä kurssilla ei käsitellä tätä mallia tämän enempää; kiinnostuneet löytävät lisätietoja epälineaarisista DY-systeemeistä muista lähteistä (esim. [B, luku 9]).
13.3 Korkeamman kertaluvun DY:n yhteys 1. kl:n DY-systeemeihin
Kertaluvun lineaarinen DY voidaan muuttaa ensimmäisen kertaluvun DY-systeemiksi, jossa on
yhtälöä.
Vakiokertoiminen yhtälön (1. kl:n) lineaarinen DY-systeemi, jossa on
tuntematonta funktiota, voidaan muuttaa
:nnen kertaluvun lineaariseksi DY:ksi.
Huomatutuksia:
- Tällä kurssilla on opittu ratkaisemaan joitakin 2. (ja eräitä korkeammankin) kertaluvun DY:itä.
- Näillä keinoilla päästään ratkaisemaan myös joitakin DY-systeemejä.
- Voitaisiin myös toimia toisin: opiskella DY-systeemien käsittelyä tarkemmin ja ratkaista 2. ja korkeamman kl:n DY:itä palauttamalla ne 1. kl:n DY-systeemeiksi.
- Kiinnostuneet löytävät tämän lähestymistavan esim. kevään 2018 kurssimateriaalista.
- (Lineaarialgebran työkalut käytössä: matriisi, determinantti, ominaisarvot ym.)
- Kiinnostuneet löytävät tämän lähestymistavan esim. kevään 2018 kurssimateriaalista.
- Numeerisia menetelmiä on sekä DY-systeemeille että korkeamman kertaluvun DY:ille.
- Huomaa, että numeeriset menetelmät ovat käytettävissä myös epälineaarisille yhtälöille.
- Usein korkeamman kl:n DY palautetaan 1. kl:n systeemiksi, jonka numeerinen ratkaiseminen sujuu samaan tapaan kuin kohdassa 6.3 nähtiin.
- Esim. Eulerin menetelmässä systeemin
iteraatiokaava olisi
- Esim. Eulerin menetelmässä systeemin
13.3.1 Esimerkkejä
- Muuta 3. kl:n lineaarinen DY
ensimmäisen kertaluvun DY-systeemiksi.
- Ratkaisu:
- Merkitään
,
ja
. Nyt
ja alkuperäinen DY on näillä merkinnöillä
Saamme (kolmen tuntemattoman ja kolmen yhtälön) 1. kl:n differentiaaliyhtälöryhmän
- Merkitään
- Muuta lineaarinen 1. kl:n DY-systeemi
(toisen kertaluvun) differentiaaliyhtälöksi ja ratkaise se. Mikä on DY-systeemin ratkaisu?
- Ratkaisu:
- Eliminoidaan toinen tuntemattomista:
- Ratkaistaan ensimmäisestä yhtälöstä
, jolloin saadaan
ja derivaatta
Sijoitetaan nämä toiseen yhtälöön, jolloin saadaan
eli
- Ratkaistaan ensimmäisestä yhtälöstä
- Ratkaistaan saatu 2. kl:n DY
:
- Karakteristisen yhtälön
juuret ovat
ja
, joten DY:n yleinen ratkaisu on
.
- Karakteristisen yhtälön
- Selvitetään vielä
:
- DY-systeemin ratkaisu on siis
- Eliminoidaan toinen tuntemattomista:
14. DY-systeemeistä, osa II
- autonominen systeemi
- ratkaisun rata
- kriittinen piste
[B, 9.2]
14.1 Autonominen DY-systeemi
- DY-systeemi on autonominen, jos muuttuja
ei esiinny yhtälöissä yksinään:
- Esimerkiksi lineaarinen, homogeeninen, vakiokertoiminen DY-systeemi
on autonominen.
- Esimerkiksi lineaarinen, homogeeninen, vakiokertoiminen DY-systeemi
14.1.1 Ratkaisun rata
Oletetaan, että autonomisella systeemillä on ratkaisu
Tämä on parametrisoitu käyrä
-tasossa; sanomme käyrää ratkaisun radaksi.
- Vrt. hiukkasen paikka
-koordinaatistossa, kun systemin (AS) yhtälöt kuvaavat hiukkasen nopeutta.
- Autonomisen systeemin ratkaisujen radat joko yhtyvät tai eivät leikkaa lainkaan.
- Tätä ominaisuutta ei ole ei-autonomisen systeemin ratkaisujen radoilla.
- Jos parametri
saadaan eliminoitua, parametrisoidun käyrän esityksestä saadaan tasokäyrän yhtälö.
- Tarvittaessa ks. Calculus 3, luku 8.
- Parametrin kadotessa katoaa myös tieto siitä, miten ratkaisu käyttäytyy ajan kuluessa.
- Jos
, voidaan ratakäyrää etsiä suoraan DY-systeemin (AS) yhtälöiden avulla:
- Tämä on 1. kl:n DY funktiolle
:
- Tämän DY:n ratkaisujen
kuvaajat ovat DY-systeemin (AS) ratkaisujen radat.
- Tämän DY:n ratkaisujen
- Oletus
takaa, että "käyrä ei käänny pystyyn" ja käyrä on (oletuksen voimassaollessa) funktion kuvaaja,
.
- Tämä muoto sopii erityisesti ratakäyrän tangentin kulmakertoimen selvittämiseen.
- Sellaisten pisteiden
lähellä, joissa
, voidaan etsiä käyrän normaalin kulmakerrointa muodon
kautta, jos
.
- Entä ne pisteet, joissa
ja
?
- Entä ne pisteet, joissa
- Sellaisten pisteiden
- Tämä on 1. kl:n DY funktiolle
14.1.2 Kriittinen piste
Pistettä, jossa ja
, sanomme autonomisen DY-systeemin (AS)
kriittiseksi pisteeksi.
- Jos
on systeemin (AS) kriittinen piste, niin systeemillä on ratkaisu
(vakiofunktiot).
- Tämä on ainoa ratkaisu, jonka rata kulkee ko. pisteen kautta.
- Vakioratkaisun rata on ko. piste.
- Kriittisiä pisteitä voi olla useita.
- Tämä on ainoa ratkaisu, jonka rata kulkee ko. pisteen kautta.
- Jos
ja
, kun
, niin sanomme, että ratkaisu
lähestyy kriittistä pistettä.
- Jos kaikki lähellä olevat ratkaisut lähestyvät kriittistä pistettä, kun
, niin sanomme, että kriittinen piste on asymptoottisesti stabiili.
- Jos lähellä olevat ratkaisut eivät pakene ajan kuluessa kauas kriittisestä pisteestä, sanomme, että kriittinen piste on stabiili.
- Asymptoottisesti stabiili kriittinen piste on stabiili.
- Jos kriittinen piste ei ole stabiili, sanomme, että se on epästabiili.
- Jos kaikki lähellä olevat ratkaisut lähestyvät kriittistä pistettä, kun
Esimerkki
- Toisen kertaluvun DY
jossa
kuvaa kappaleen paikkaa 1-ulotteisessa koordinaatistossa, kun kappaleen massa on
ja siihen vaikuttaa voima
,
voidaan merkinnän(= kappaleen nopeus) avulla kirjoittaa DY-systeeminä
- Tämän systeemin kriittisessä pisteessä sekä nopeus (
) että kiihtyvyys (
) ovat nollia.
- Kappale on levossa eikä siihen vaikuta mikään voima.
- tasapainotila
- Tämän systeemin kriittisessä pisteessä sekä nopeus (
- Miten käy, kun kappale siirretään pois tasapainotilasta?
- Jos kriittinen piste on
- asymptoottisesti stabiili, kappale palaa tasapainotilaan,
- epästabiili, kappale pakenee kauas tasapainotilasta,
- stabiili, mutta ei asymptoottisesti stabiili, kappale jää liikkumaan lähistölle.
- Vrt. heiluri jäykän varren päässä
- tasapainoasema ala-asennossa, ilmanvastus huomioidaan
- tasapainoasema ylä-asennossa
- tasapainoasema ala-asennossa, ilmanvastusta ei huomioida.
- Jos kriittinen piste on
Huomautuksia/lauseita
- Kunkin tason pisteen kautta kulkee korkeintaan yksi systeemin (AS) ratakäyrä.
- Jos ratakäyrä kulkee vähintään yhden sellaisen pisteen kautta, joka ei ole kriittinen piste, niin käyrä joko ei leikkaa itseään lainkaan tai on suljettu käyrä (esim. ellipsi).
- Suljettua ratakäyrää vastaava systeemin (AS) ratkaisu on jaksollinen.
- Jos systeemi (AS) kuvaa hiukkasen paikkaa
-koordinaatistossa ja hiukkanen on alkuhetkellä muualla kuin kriittisessä pisteessä, se ei päädy äärellisessä ajassa kriittiseen pisteeseen
- eli ratakäyrä voi "päättyä" kriittiseen pisteeseen, mutta ei "ohittaa sitä".
- Hiukkanen
- liikkuu samaa rataa pitkin riippumatta alkuhetkestä;
- ei palaa lähtöpisteeseensä paitsi jaksollisen ratkaisun tilanteessa, jolloin se palaa sinne toistuvasti;
- ei leikkaa toisesta pisteestä lähteneen hiukkasen rataa, elleivät ne ole samalla radalla;
- voi päätyä kriittiseen pisteeseen vain kun
.
- Ratkaisu voi käyttäytyä kolmella eri tavalla:
- lähestyy kriittistä pistettä, kun
- rata on suljettu käyrä (ja ratkaisu siis jaksollinen) tai rata lähestyy suljettua käyrää
- ratkaisu pakenee (äärettömän kauas), kun
.
- lähestyy kriittistä pistettä, kun
- Tarkemmin: kevään 2018 kurssin TIM-sivulla
14.1.3 Esimerkkejä
- Ratkaise alkuarvotehtävä
Miltä ratkaisun rata näyttää ja mikä on sen etenemissuunta, kun
kasvaa?
- Ratkaisu:
- Yhtälöparin ensimmäisessä yhtälössä ei esiinny
eikä jälkimmäisessä
, joten kumpikin yhtälö voidaan ratkaista separoimalla ja ratkaisut ovat
- Alkuehdoista saadaan
- Ratkaisun rata on parametrisoitu käyrä
- Eliminoidaan parametri
:
- Rata on siis käyrä
,
,
(puolikas ylöspäin aukeavaa paraabelia, jonka huippu on origossa).
- Rata on siis käyrä
- Kun
, saadaan alkuehdoista
ja
, ja kun
kasvaa, rata lähenee origoa.
- Ratkaisematta systeemiä nähdään, että kun
ja
, niin
ja
.
- Ratkaisematta systeemiä nähdään, että kun
- Huom: systeemillä on yksi kriittinen piste, origo; alkuehdot toteuttava ratkaisu lähenee origoa, kun
.
- Yhtälöparin ensimmäisessä yhtälössä ei esiinny
- Ratojen etsiminen toisella tavalla:
- Kun
, radan tangentin kulmakerroin on
- Tämä on separoituva yhtälö
, jonka ratkaisut ovat
eli
- Alkuehdoista
ja
saadaan
.
- Ratkaisematta systeemiä nähdään, että kun
ja
, niin
ja
eli radan etenemissuunta on alas vasemmalle.
- Ratkaisematta systeemiä nähdään, että kun
- Kun
- Etsi systeemin
kriittiset pisteet sekä ratkaisujen radat.
- Ratkaisu:
- Systeemin kriittiset pisteet ovat pisteet
, joille
eli pisteet, joissa
sekä piste
.
- Systeemin ratkaisujen radat (kriittisten pisteiden ulkopuolella) saadaan yhtälöstä
- Yhtälö
on separoituva ja sen ratkaisut ovat
eli
- Ratkaisujen kuvaajat ovat
-säteisiä
-keskisiä ympyröitä tai niiden osia (ei-vakioradat ovat kriittisten pisteiden ulkopuolella).
- Yhtälö
- Systeemin kriittiset pisteet ovat pisteet
Lisähuomioita
- Sama idea kuin esimerkin 1 toisessa tavassa sopii myös epälineaarisen autonomisen 1. kl:n DY:n tutkimiseen.
- esim. yhtälöstä
saadaan merkinnällä
funktio
ja jos
, tämän kuvaaja on alaspäin aukeava paraabeli.
- Kriittiset pisteet ovat
ja
.
- Näistä
on epästabiili ja
asymptoottisesti stabiili; tämä nähdään derivaatan merkistä
- positiivinen, jos
ja
- negatiivinen, jos
.
- positiivinen, jos
- Näistä
- Tämä kyseinen yhtälö voidaan myös ratkaista separoimalla; ratkaisuksi saadaan
- Kriittiset pisteet ovat yhtälön vakioratkaisuja.
- (Vrt. logistinen yhtälö, Calculus 2, kohta 5.2.3.)
- Entä, jos
ja
?
- esim. yhtälöstä
Tässä käsitellään “yhden yhtälön systeemiä”, jonka kriittiset pisteet ovat ne kohdat x, joissa x’ = 0, kuten tekstissä on kerrottu. Pahoittelen pientä hämmennystä videon tässä kohdassa.
—- Lotkan ja Volterran peto-saalis -mallissa
- kriittiset pisteet ovat
ja
- kun alkuehdot ovat
,
(kriittisen pisteen ulkopuolella), ratkaisut ovat jaksollisia ja pysyvät positiivisina
- (ei todisteta; kiinnostuneet löytävät käsittelyn muista lähteistä, esim. [B, 9.5] tai Braun).
- kriittiset pisteet ovat
Kertaus
- Varsinaista kertausluentoa ei ole, mutta voit esittää kysymyksiä esim. Ratkomon kanavalla; päivystän vielä maanantaina 17.5. klo 14--16. Toki myös muuna aikana saa tavoitella.
Ohjeita:
- Älä stressaa liikaa.
- Jos olet osannut yli puolet jokaisen viikon harjoitustehtävistä, pääset kyllä kurssitentistä läpi.
- Jos et ole, keskity kohtaan 2.
- Varmista, että osaat perusasiat; esim.
- tunnistat ja osaat ratkaista
- separoituvan DY:n
- lineaarisen 1. kl:n DY:n
- Mitä eri tapoja on? Mikä on helpoin, milloin se toimii? Onko menetelmää, joka toimii aina?
- lineaarisen 2. kl:n DY:n
- Eri menetelmiä eri tilanteisiin: vakiokertoiminen, Eulerin yhtälö, muu...
- Missä tilanteessa voit käyttää kertaluvun pudotusta?
- Miten HY:n ratkaisua voi käyttää TY:n ratkaisemiseen?
- Eri menetelmiä eri tilanteisiin: vakiokertoiminen, Eulerin yhtälö, muu...
- helpot erikoistapaukset
- Ratkeaako suoraan integroimalla?
- Palautuuko alempaan kertalukuun muuttujanvaihdolla
?
- hiukan hankalammat erikoistapaukset
- Palautuuko DY muuttujanvaihdolla separoituvaksi? Miten?
- eksakti DY
- tiedät, mitä yleinen ratkaisu tarkoittaa
- tiedät, mistä vapaat vakiot ratkaisuun ilmestyvät ja osaat käsitellä niitä
- tiedät, mitä implisiittinen ratkaisu tarkoittaa
- tiedät, mitä alkuarvotehtävä tarkoittaa ja miten se ratkaistaan
- osaat tarkistaa saamasi ratkaisun
- osaat lukea ja ymmärtää erilaisia merkintöjä ja käyttää niitä oikein
- lasket oikein
- tunnistat ja osaat ratkaista
- Mieti, osaatko vielä muutakin.
- käyräparven DY ja kohtisuorat leikkaajat
- numeeriset menetelmät, viivaelementtikenttä
- korkeamman kl:n vakiokertoiminen lineaarinen DY
- DY-systeemit
- sarjaratkaisun etsiminen lin. 2. kl:n DY:lle (myös säännöllisen singulaaripisteen lähellä)
- hankalammat erikoistapaukset
- Palautuuko DY muuttujanvaihdolla johonkin tuttuun tapaukseen, esim. lineaariseksi?
- Palautuuko DY eksaktiksi integroivan tekijän avulla?
- Mitä muita "temppuja" epälineaaristen DY:iden ratkaisemiseksi on?
- käytännön sovellukset
- DY-mallin rakentaminen annetuista tiedoista
- eksponentiaalinen kasvu / väheneminen
- harmoninen värähtelijä
- teoreettisten tulosten perustelut
- Huom: useimmat asiat voi yrittää ymmärtää, jolloin muistamista on vähemmän.
- esim.
- Mitä separointimenetelmässä oikeastaan tehdään?
- Mistä karakteristinen yhtälö tulee, millainen yleinen ratkaisu sen avulla saadaan - ja miksi?
- Miten epähomogeenisen lineaarisen DY:n
- yleinen ratkaisu löytyy HY:n yleisen ratkaisun avulla - ja miksi?
- yksittäisratkaisun etsimisen voi "paloitella", kun epähomogeeninen osa on summa - ja miksi?
- Toisaalta joskus voi ensin oppia muistamaan - ja ymmärrys kehittyy pikkuhiljaa myöhemmin, kun kokemus karttuu.
- (Vrt. toisen asteen yhtälön ratkaisukaavan käyttäminen vs. johtaminen neliöksi täydentämällä.)
- esim.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.