auto_number_headings: true
heading_format:
1: '{text}'
2: '{h2}. {text}'
3: '{h2}.{h3} {text}'
4: '{h2}.{h3}.{h4} {text}'
5: '{h2}.{h3}.{h4}.{h5} {text}'
6: '{h2}.{h3}.{h4}.{h5}.{h6} {text}'
global_plugin_attrs:
csPlugin:
anonymous: true
all:
anonymous: true
resetText: Reset
#button: Save
lang: en
lazy: false
css: |!!
.kuvavasen img {
display: block;
margin: 0;
}
.kuvavasen p.caption {
margin-left: 5em;
margin-top: -2em;
text-align: left;
}
span.iso {
font-size: xx-large;
font-weight: bold;
}
.htmlresult {
text-align: left;
margin-left: 1em;
}
!!TIM and Math
Vesa Lappalainen / Faculty of Information Technology
Go to: r.jyu.fi/tmath
or show this to mobile
What is TIM?
The Interactive Material
- TIM is an open source cloud-based platform to make interactive documents like
- lecture notes / eBooks
- weekly exercises
- exams
- manuals
- workbook
- discussions
- write together and share
- For:
- normal lectures
- peer instruction
- self studying
- MOOC
- Flipped Classroom
- whatever
Properties
- mark as read (red for unread, click away, yellow for changed block)
- lecture mode (real time questions, lecture wall)
- correction phrases
- comments (public/private)
- see all answers from the user, not just the last one
- group answering
- automatic assessment for some task types
- keep original and translated document in sync
- gamification
Examples of interactions
This is examples for slow devices. One must take cursor over the task to get it open.
1. Videos
2. Textual answers
#
text1
3. Textual answers with automatic assessment
#
number3
4. Return image
In a math assignment, it may be reasonable to write things to paper and return an image of that
#
image2
5. Multiple choices
#
mcq31
#
Howmany
How many boxes
Open plugin
#
Vaaka
Weight
Open plugin
6. Write the problem
More than asking the final result, ask the formula and let computer to do the calculations:
#
sageV
7. Image dragging
#
prosessit3
#
imagex172
#
Plugin2
#
vapaa1
8. TeX writing
One can write math by TeX:
#
mp1
.
#
writemath2
9. GeoGebra
- see more from TIM and GeoGebra
#
geo
10. Octave
#
esim5_6
11. Maxima
- see Tim and Maxima
#
maxima1
#
maxima2
#
maxima3
- see Maxima
12. MathCheck by Antti Valmari
#
seq1
- see MathCheck
13. Sage math
#
sageP1
#
sageP11
#
sage1
#
sage2
14. Embedded pages
- TODO: This should be faund a new eaxmple.
15. JavaScript
#
jsLumiukkoUusi
#
vpython2
#
jsIntegraali
Linear
#
jsMokki1
16. For smaller children
#
lauseke
#
jsLauseke
17. Statistics
#
rData1
#
sageP02
#
sageP05
#
sageP07
18. GlowScript
See GlowScript
#
vpython14
#
vpython4
19. Java
#
javagra3D
20. Math.js
See Math.js.
#
css1
21. Stack
- also with JSXGraph
- look more from Stack-examples
#
jsxsin
#
visjs3D
23. JSXGraph
#
jsx1
#
jsx2
#
jsx3
#
py10-4
#
Plugin1
25. Write Math
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.
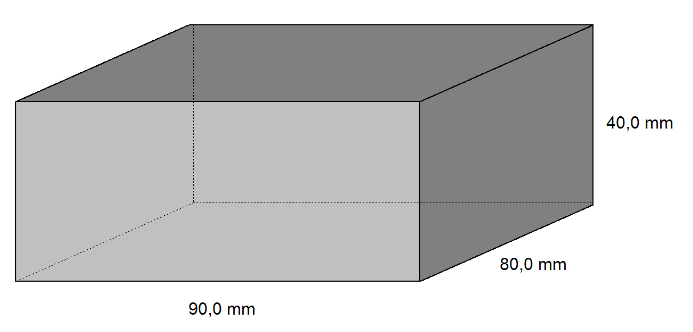 Count mass of the aluminium piece that has density of
Count mass of the aluminium piece that has density of